【導讀】本文詳解控制理論。通常我們在講解控制理論時,都只通過框圖,而不參考實際的電路。在數學和電路仿真工具的幫助下,我們將一步步說明電子控制理論與現代電路設計息息相關。
簡介
大學教授的許多科目都會令學生發問:"學習這門課程能讓我找到一份工作嗎?"控制理論可能就是這樣一門課程,這些多達數頁的數學和框圖不會在實際電路中被直接使用。但是,控制系統教授工程師如何設計自動系統、系統距離實現穩定操作還有多大距離,以及如何從給定系統獲得最佳響應。因為不管課程是關于機械、電氣、土木、航空,或者是通信工程,如果系統不穩定,一切都沒有用。
對于設計工程師來說,控制理論就是生命本身。
現在有許多關于控制理論的優秀文章,但是其中很多都是借助框圖,以最概括化的方法來進行介紹。本文主要面向電子工程師,從電路分析和仿真的角度介紹電子控制系統;介紹了常見的二階系統背后的理論,而且是利用有效的電路示例來加以說明;旨在揭露二階系統的基礎原理,并向嘗試了解電子控制理論的人員說明,該理論與模擬電路設計之間存在關聯。
二階系統
圖1所示為最基礎的二階網絡。
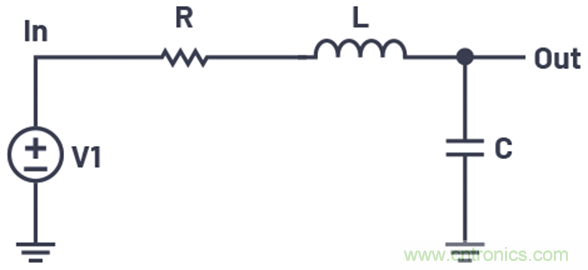
圖1.由一個電阻、一個電感和一個電容構成的二階網絡。
其傳遞函數為:

方程1右側的分母被稱為 特征多項式 ,如果我們令特征多項式為0,我們會得出 特性方程。當轉換函數的分母等于0時,得到系統的極點 通過求解特性方程的根(讓特性方程等于0的s的值),我們可以找到系統的極點,從而獲取與系統運行狀況相關的許多信息。
二階系統傳遞函數的一般形式為:
其中ζ表示阻尼系數,ωn表示電路的固有振蕩頻率(或無阻尼頻率),單位為弧度/秒。
所以,二階系統的一般特性方程為:
比較方程3和方程1,我們可以看出,圖1中的電路的固有頻率為:
我們也可以看出,電路中的電阻會影響網絡的阻尼系數:
所以
所以
可以直觀看出,如果電路中沒有電阻,網絡不會出現耗損(無阻尼),如果模擬這種電路,則電路會永久振蕩。隨著電阻增加,振蕩會更快衰減。
圖2顯示一個RLC電路,其中階躍輸入為1 V,L = 1 µH,C = 1 µF,電阻分別為0 Ω、100 mΩ和500 mΩ。電路按照預期的159 kHz頻率振蕩。電阻增加對衰減的影響一目了然。
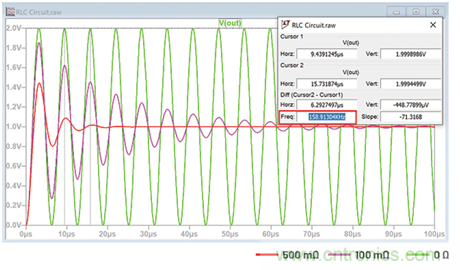
圖2.電阻對網絡振蕩的衰減影響。
我們可以通過將拉普拉斯域轉換為時域,以數學方式展示圖2所示的模擬結果。拉普拉斯域中的單位階躍輸入寫為:
所以當我們使用單位階躍輸入仿真二階系統時,結果會變成:
如果使用部份分式分解法,方程9可以寫為:
方程10是表示在拉普拉斯域中的。
在時域中,這會轉換為:
其中
采用逆拉普拉斯變換的公式11的數學推導如 附錄A所示。
通過公式11,我們可以看出圖1的電路如何響應階躍輸入。我們可以看到,波形具有與正弦曲線類似的特性,其幅度則由e–ζωnt項調制,根據阻尼系數是正數或復數出現指數式衰減或增加。近似來看,響應由正弦部分和余弦部分組成,但是,阻尼系統較低時,正弦部分非常小。
此外,盡管電路的固有頻率為ωn,但電路不會按照此頻率振蕩,而是按照更低一些的頻率ωdn決定。
要找出轉換函數的極點,則需要確定轉換函數何時等于0,也就是說:
s的值可以使用二次方程求解:
其中
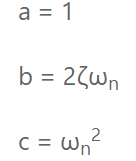
要得出系統極點,需要:
如果阻尼系數小于1,會得出負的平方根,所以最好將方程15寫作:
我們之前說過 ωd = ωn√(1 – ζ2),所以方程16可以改寫為:
這里我們可以看出,系統的極點包含實數部分(–ζωn) 和虛數部分 (±jωd)。
方程17可以求解得出特性方程的根(系統的極點)。我們如何將這些極點與系統的穩定性聯系起來?現在我們需要把拉普拉斯域的極點和時域的穩定性聯系起來。
通過方程11和方程17,我們可以得出以下觀察結果。
無阻尼固有頻率ωn決定了:
拉普拉斯域(方程17)中的極點 (–ζωn)的虛數部分。
振蕩的實際頻率
由此,可以合理假設極點的虛數部分確定了系統振蕩的實際頻率。
這兩個假設可以用s平面圖表示,我將在下一節詳細介紹。
穩定的系統
控制理論認為,如果極點位于s平面的左半部分,則系統是穩定的。圖3所示為一個s平面示例,其中實數部分在x軸上繪制,虛數部分在y軸上繪制。
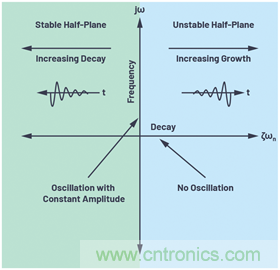
圖3.s平面:顯示穩定的左半部分和不穩定的右半部分。
從方程17可以看出,如果阻尼系數為正(方程17的實數部分為負),則極點位于左半部分。隨著阻尼系數增加,方程17的極點進一步向左移動(在左側平面內,越來越靠近左側)。
如果方程17在拉普拉斯域中,如何在時域中轉換?
為了方便起見,我們再次使用方程11:
正阻尼系數ζ會引發指數式的衰減幅度響應(由e–ζωnt項表示),阻尼越大,衰減越快。隨著阻尼系數增加,極點進一步向左移動(在拉普拉斯域內),這進一步增大了時域內的指數式衰減。從圖2中可以看出這一點,圖2使用100 mΩ和500 mΩ線路來表述電阻對阻尼的影響。在此區域中,500 mΩ線路的阻尼系數最大,所以它的指數式衰減最明顯。0 Ω時,阻尼系數為0,此時極點完全位于y軸上,電路無限振蕩,如圖2中的綠色線路所示。
值得注意的是,即使系統是穩定的,這并不表示一定沒有振蕩。電路可能會在左半平面的極點處振蕩,但是這些振蕩的振幅會隨著時間而衰減,如圖2所示。
這對圖1中的電路意味著什么?
我們知道圖1中的阻尼是通過下方的方程得出:
它的固有頻率則是:
所以,在L = 1 µH,C = 1 µF時,固有頻率為1 Mrads–1 (= 159.1 Hz),R = 500 mΩ時的阻尼系數為0.25。
所以,阻尼振蕩頻率ωd由以下方程計算得出:
所以,阻尼振蕩頻率為968 krads–1,即154 kHz。這可以通過查看圖4中紅色波形的頻率來說明。
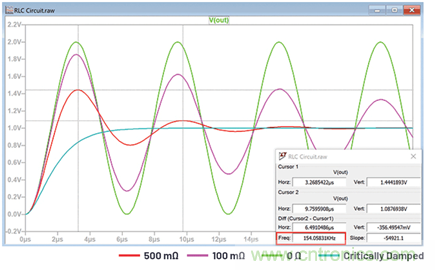
圖4.阻尼對RLC電路振幅和頻率的影響。
正弦波的振幅按e–ζωnt衰減。阻尼系數為0.25,固有頻率ωn為1 Mrads–1,阻尼固有頻率為968246 rads–1,那么方程11變成:
使用這個公式,計算得出VOUT在3.26 μs時為1.44 V,在9.75 μs時為1.09 V,與圖4中顯示的讀數完全一致。
圖4清楚顯示了增加阻尼系數會產生的影響,即振幅和阻尼固有頻率都減小。
如果我們繼續增大阻尼系數,會出現什么結果?
我們知道阻尼固有頻率是通過以下方程計算得出:
當阻尼系數增大到一時,阻尼固有頻率減小到零。這就是所謂的臨界阻尼點,此時電路中的所有振蕩終止。這一點可參見方程11。自阻尼固有頻率ωd減小到0,正弦項等于0,余弦項目等于一,表達式簡化為一階系統,與通過電阻充電的電容完全一樣。
這一點可以參見圖4中的臨界阻尼線路。
不穩定系統
由于所有電路都具有電阻,所以許多電子控制電路的極點都位于左半平面,且系統本身保持穩定。但是,由方程11可以看出,負阻尼系數會導致振幅響應呈指數增長,所以極點位于右半平面會導致系統不穩定。在電路模擬中,通過插入負電阻,可以很容易看出右半平面的影響。圖5顯示RLC電路,其電阻為負。
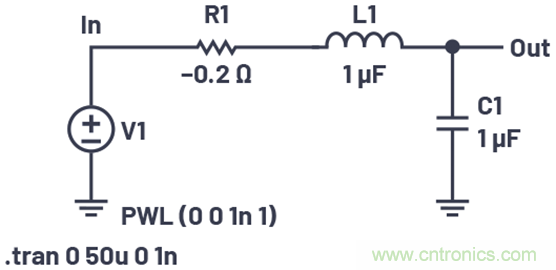
圖5.電阻為負的RLC電路。
該電路的阻尼系數為-0.1。圖6顯示了它對階躍輸入的響應。
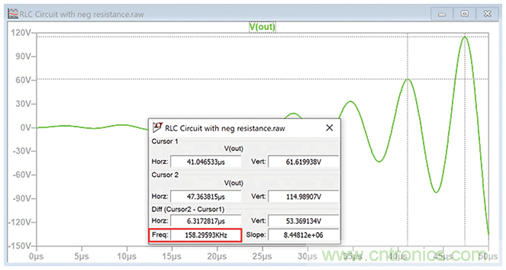
圖6.阻尼為負的二階系統的階躍響應。
阻尼固有頻率仍然由以下方程表示:
阻尼系數為-0.1時,振蕩的實際頻率為994987 rads–1 (158.3 kHz)。
同樣,從方程11可以看出電路響應由以下公式表示:
在輸出增大時,我們可以得出振幅響應:VOUT在41.05 μs時,計算得出的值為61.62 V,在47.36 μs時,為114.99 V,與圖6中所示的讀數完全一致。
主導極點
有時一個系統由許多極點組成,使分析變得復雜。但是,如果極點之間相隔的距離足夠大,那么一個極點產生的影響會占主導,因此可以忽略非主導極點,從而簡化系統。
圖7的上半部分顯示了兩個RLC電路,每個都使用完全相同的L和C元件;只是電阻發生了變化。電阻較低的電路的極點更靠近s平面的虛數軸。
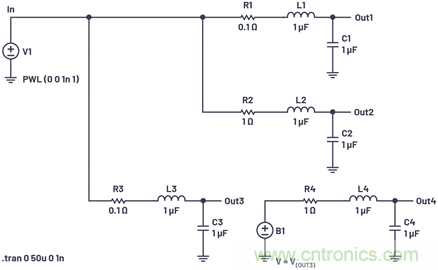
圖7.主導極點的位置對串聯和并聯電路的影響。
圖7的下半部分顯示了這兩個電路的串聯。我們使用行為電壓源B1來復制V(OUT3),以免它被R4、L4和C4加載,以便我們查看V(OUT3) × V(OUT4)的真實響應。
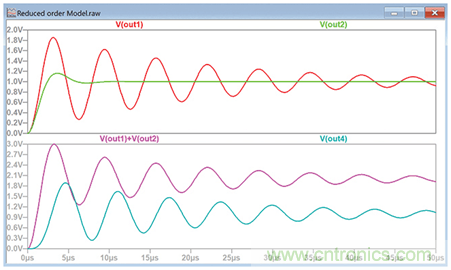
圖8.當兩個波形相加或相乘時,主導極點對系統響應的影響。
我們可以參考圖8查看它們的響應。不出所料,電阻最大的電路具有最大的阻尼系數,因此其振蕩衰減也最快,如圖V(OUT2)所示。但是,我們注意到,當兩個輸出要么相加(使電路并聯),要么相乘(使電路串聯)時,V(OUT1)在響應中占主導。因此,要簡化復雜的系統,方法之一是重點關注極點更靠近jω軸的電路,該電路會主導整個系統的響應。
在左右半面均有極點分布的系統
我們已經考慮過極點位于左半平面或右半平面的系統。如果系統在左右半面均有極點分布,會怎么樣?哪一種在穩定性方面更勝一籌?為什么?
我們再次參考方程11,可以看出指數是決定系統是否穩定的決定因素。我們可以忽略方程11的正弦部分,只看指數,以了解如果我們將左半面的極點和右半面的極點結合,會發生什么。圖9通過一個簡單電路來進行演示。
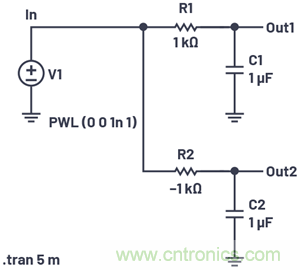
圖9.極點分別位于左半面和右半面的電路。
很顯然,頂部的RC電路的極點位于左半面,因為它的電阻為正。底部電路的極點則位于右半面。得出此結論的數學推導如 附錄B所示。
圖9中,電路的響應如圖10所示。
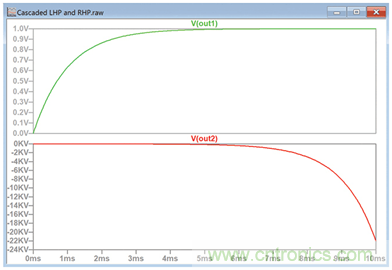
圖10.對具有正負電阻的RC電路的階躍輸入的響應。
頂部波形在大約5毫秒后穩定在零梯度,這符合大眾接受的規則,即RC電路將穩定在大約5個時間常數。相反,V(OUT2)的梯度不斷增加?,F在可以明顯看出,如果將極點位于左半面的電路和極點位于右半面的電路串聯,那么整個電路會不穩定,這是因為在左半面電路穩定很長時間后,右半面電路的響應會繼續呈指數上升。因此,為了讓電路穩定,所有極點都必須位于左半面。
結論
本文將電子控制理論中使用的理論模型與電子工程師所處的現實聯系起來。受系統中的電阻(或阻尼)影響,只有當所有極點都位于左半面時,控制系統才會保持穩定。對于極點位于右半面的系統,通過測量其輸出響應,結果證實存在問題,因為這需要構建負電阻模型。幸好,計算機模擬幫我們解決了這個問題,讓我們能夠通過簡單變更電阻的極性來展示穩定和不穩定的電路。
同樣,拉普拉斯變換也很少在課堂之外出現,但在驗證二階電子系統如何工作時,它們的作用可謂是無價的。
附錄A
顯示
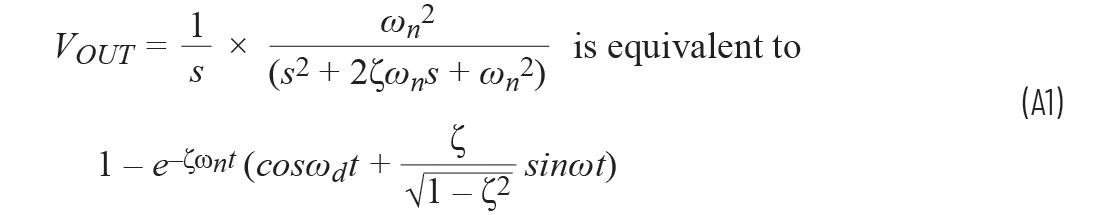
單位階躍輸入的拉普拉斯變換為
二階低通濾波器的通用轉換函數為
所以,由單位階躍模擬的二階系統的響應為
使用了標準的部份分式分解法,方程如下:
用s代替x之后,
在A4中,分子中不含s或s2。而且,分母中也不含a。
所以方程A6可以改寫為
因此
為保證方程A8兩邊的分母相同,可以將其改寫為
為了驗證,可以將方程A9的右側與方程A8的右側進行比較:
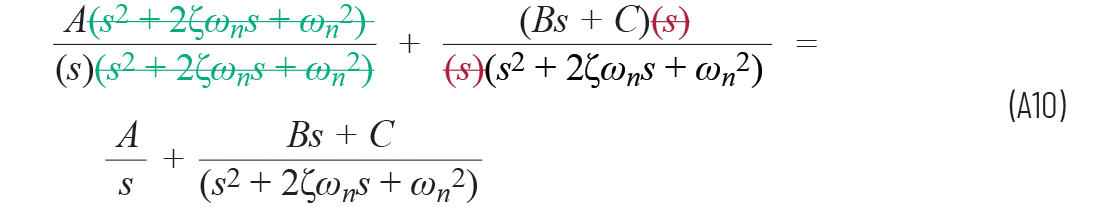
現在,我們可以使方程A9的分母相等,以求解A、B和C:
s2的系數相等:
0 = A + B
s1:的系數相等:
0 = A(2ζωn) + C
s0:的系數相等:
ωn 2 = Aωn 2
所以A = 1, B = –1, C = –2ζωn
因此,通過方程A8可以得出
(注意符號的變化,因為B和C都為負)
從時域(左邊)到拉普拉斯域(右邊)有三次變換:

通過完成平方計算,我們可以把方程A12寫為
等于
我們現在需要讓分子等于 (s + 2ζωn) ,使其與分母中的第一項匹配,以便我們使用拉普拉斯定義:
因此,通過將ζωn分子項分解為分式,方程A15等于
(所以, a = –ζωn b = ωn√(1 – ζ2))
我們現在需要讓方程A17的第三個項等于ωn√(1 – ζ2) ,使其和分母匹配,以便我們使用拉普拉斯定義:
用方程A17的第三個項除以 ωn√(1 – ζ2),然后將 ωn√(1 – ζ2)放在分子位置。
那么整個方程可以改寫為
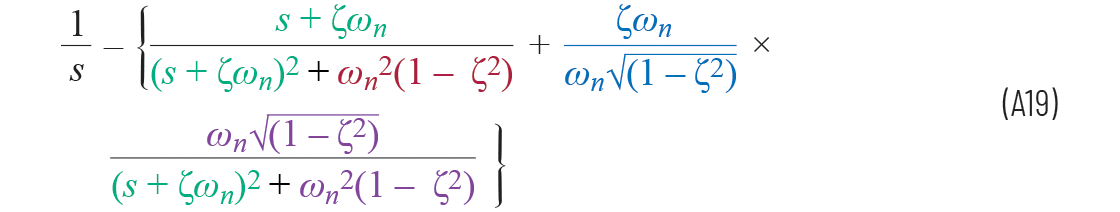
所以 a = –ζωn b = ωn√(1 – ζ2)
方程A19現在可以從拉普拉斯域中轉變為
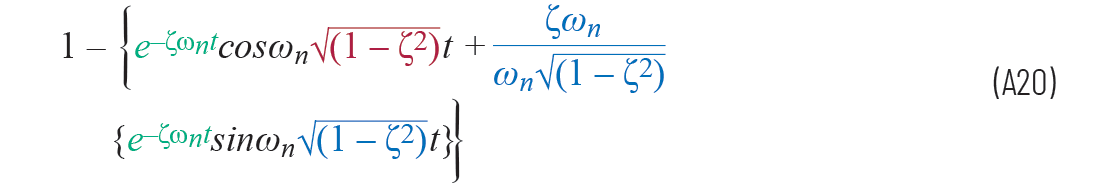
第三項中取消了兩個wn。因為阻尼固有頻率ωd可以寫為
方程A21可以簡化為
許多課本中提到,方程A21的多項式也可以寫為
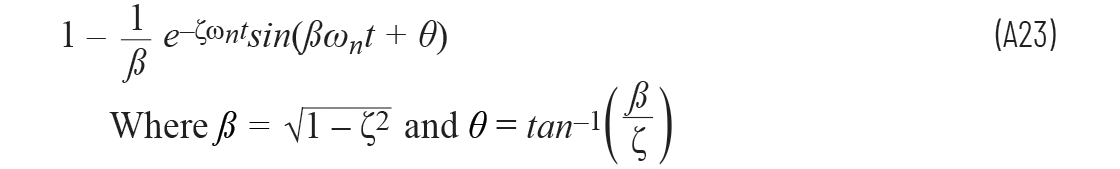
所以我們的衰減指數由阻尼系數和無阻尼固有頻率決定,振蕩由阻尼固有頻率決定。
可以將方程A23輸入電子表格和表示輸出與階躍輸入之間關系的圖表中。
附錄B
顯示
單位階躍輸入的拉普拉斯變換為
RC電路的通用轉換函數為:
s為負值時,分母為零,所以這個電路的極點位于左半面上,因此系統是穩定的。如果電阻為負,那么極點位于右半面,系統會不穩定。
從方程B3可以看出,RC電路的轉換函數與階躍輸入之間的關系為
使用了標準的部份分式法,方程如下:
在本例中,a = 0
所以
分子中s1 的相等項為
0 = ACR + B
分子中 s0的相等項為
1 = A
所以 A = 1, B = –CR
因此
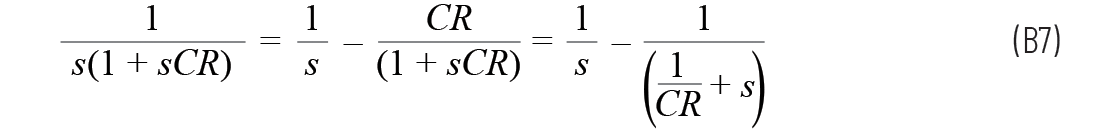
從時域(左邊)到拉普拉斯域(右邊)有兩次變換:

將方程B7轉化為采用時域意味著RC按照預期
進行響應。
附錄
下載與本文相關的 LTspice® files 文件。
欲了解有關LTspice的更多信息,請訪問analog.com/ltspice。
參考電路
Charles Phillips、Royce Harbor?!斗答伩刂葡到y》,第4版。Prentice Hall International,1988年。.
致謝
我們采用 LTspice進行模擬。
非常感謝倫敦布魯內爾大學的Maysam Abbod為本文實施理論校正。
推薦閱讀:






