【導讀】電阻(R)、電感器(L)和電容器(C)是電子學的三個基本無源元件。它們的特性和行為已經在交流電阻、交流電感和交流電容中詳細介紹過教程本文將重點討論這三個元件的串聯組合,稱為串聯RLC電路。首先,介紹了三種本構元件的交流特性,并簡要介紹了RLC電路。
串聯RLC電路
演示
RLC電路的表示如下圖1所示:
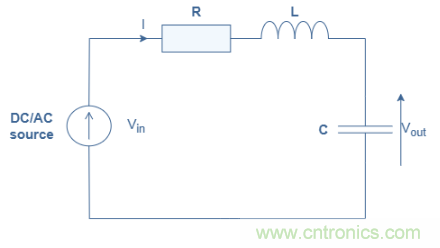
圖1:RLC系列電路示意圖
電阻器是一個純電阻元件,在其上的電壓和電流之間沒有相移。其阻抗(ZR)在直流和交流區保持不變,等于R(單位:Ω),電感是一個純無功元件,相移為+90°或+π/2rad。其阻抗由ZL=jωL給出,ω是交流情況下電壓/電流的角頻率,L是電感(單位:H)。在直流區,電感器表現為兩個端子之間的短路;在交流區,電感器的阻抗隨著頻率。電感器通常被認為是一種元件,它可以抵抗電流。電容器也是純無功元件,但其相移為-90°或-π/2rad。它的阻抗由ZC=-j/Cω給出,C是電容(單位為F),因此當頻率增加時,它在直流區表現為開路,在交流區表現為短路電壓輸入圖1,這三個組件串聯在一起。電路由直流或交流電源供電,輸出是電容器上的電壓。前面的阻抗之和是電路阻抗的總和說明:ZRLC=ZR+ZL+ZC=R+j(Lω-(1/Cω))在下一節中,我們將介紹該電路對電壓階躍(也稱為瞬態響應)的響應。
瞬態響應
在本節中,我們將重點關注圖1中所示電路的行為,當對其應用重邊步驟H(t)時:
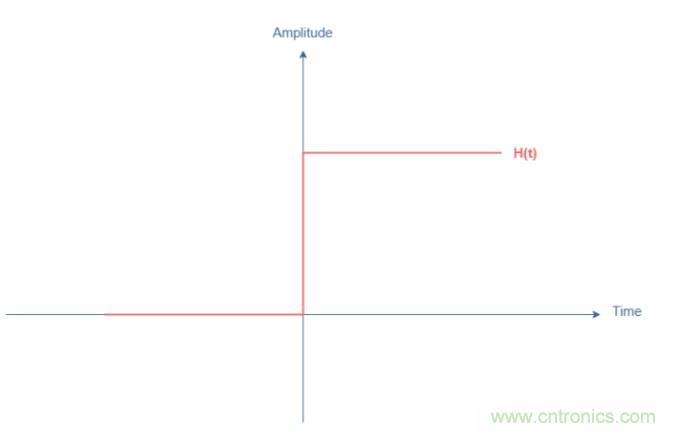
圖2:Heaviside函數說明
升程階躍的特征是t<0等于0,t>0時等于Vin。這兩種狀態之間的轉換類似于脈沖,因為當t=0時,導數趨于+∞。通過對電路進行網絡分析,我們可以得出:Vin=R×I+L×dI/dt+Vout。此外,我們知道電流可以改寫為I=C×dVout/dt,由此得到以下二階微分方程:
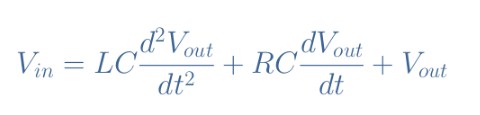
式1:串聯RLC電路的二階微分方程
這種方程的解是永久響應(時間常數)和瞬態響應Vout,tr(時間變量)的總和。永久響應的求解是一個方程1的永久解,其瞬態響應很復雜,涉及許多步驟,本文不詳細介紹。我們承認它的表達式可以有三種不同的形式,取決于Q=(1/R)√(L/C)的值,稱為電路的品質因數。另一個重要參數是ω0=1/√(LC),這是電路。何時Q> 1/2,該系統被稱為偽周期響應或欠阻尼響應,瞬態響應可采用Vout、tr=Ae-αtcos(ωt+Φ)的形式寫入。考慮電路初始條件(如果電容器充電或未充電…)可以找到常數A、α和Φ。脈動ω稱為角頻率,取決于基本頻率ω0。當Q<1/2時,該系統被稱為非周期或過采樣響應,瞬態響應形式為Vout,tr=e-αt(A1e-ωt+A2eωt),最后一種情況是Q=1/2,對應于臨界狀態或臨界阻尼響應。在這種情況下,Vout,tr=(A+Bt)e-ω0t,Vin:
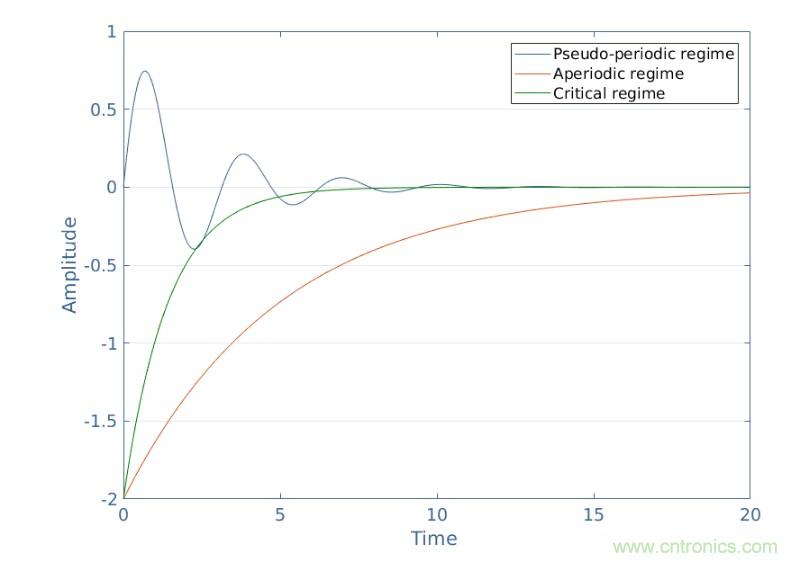
圖3:瞬態響應的不同區域曲線
當時間增加時,每條曲線趨于0。這是有意義的,因為我們知道Vout=Vin+Vout,tr和Vout(t→+∞)=Vin,因此,Vout,tr→0。但是,不同的可能瞬態響應在相同的速度和行為下不趨向于0。臨界狀態是最快趨于0的狀態,而非周期狀態是最慢的。偽周期區域呈現振幅減小的振蕩指數級的。為了一個未知的RLC電路,用最佳可能曲線識別和匹配瞬態響應,可以得到電路的重要特性,如ω0和Q。
交流響應
在本節中,我們考慮圖1中所示的同一電路,現在使用交流電源供電。利用復符號dX/dt=jωX的性質,ω是源的角頻率,我們可以用以下形式重寫方程1:
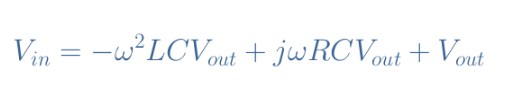
式2:串聯RLC電路的復二階微分方程
然后我們可以表示Vout/Vin的比值,這是串聯RLC電路的傳遞函數T:
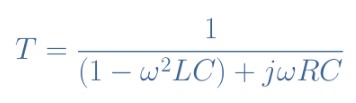
公式3:串聯RLC電路的傳遞函數
知道Q=(1/R)√(L/C),ω0=1/√(LC),并考慮參數x=ω/ω0,稱為歸一化頻率,我們可以重新整理方程3,寫出傳遞函數的標準形式,從而簡化并使表達式更緊湊:
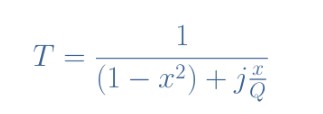
公式4:RLC電路傳遞函數的標準形式
為了獲得作為參數x的函數的電路增益,繪制傳遞函數的范數是很有趣的。本例中取了R=10Ω和20Ω,L=0.2 H,C=100μF的值:
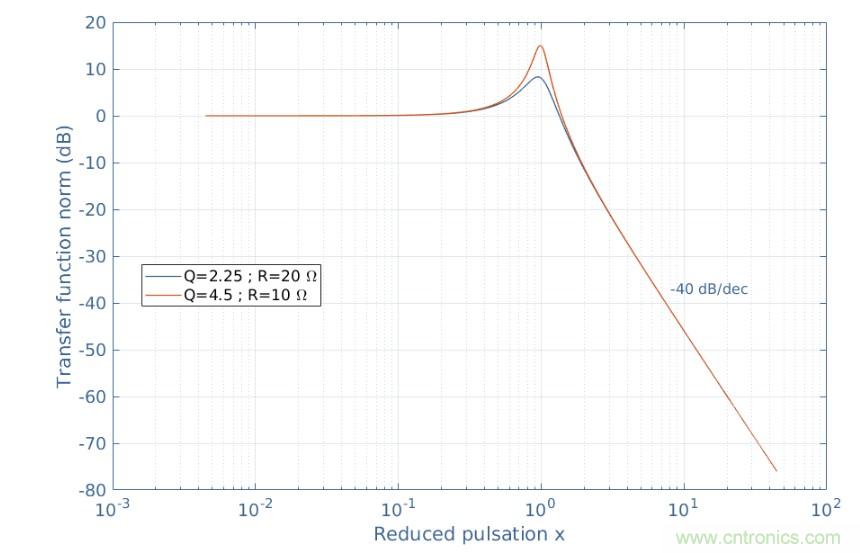
圖4:串聯RLC電路的增益
我們可以注意到,圖1中所示的串聯RLC電路在交流區起到了二階低通濾波器的作用,因為它降低了高于ω0的脈動的輸出信號,通常稱為電路。二階濾波器具有對ω0附近頻率的信號進行輕微放大的特性,并且在截止頻率之后呈現-40 dB/dec的降低,而不是僅-20 dB/dec,例如一階過濾器。它在圖4中強調了Q值(取決于R)對曲線形狀的影響。共振頻率附近的峰值確實以其帶寬Δω=ω0/Q為特征。在本例中,ω0=223 rad/s和Q=4.5或2.25,這使得橙色曲線的Δω=50 rad/s較窄,藍色曲線的帶寬為100 rad/s。因此,我們可以注意到,品質因數決定了共振是窄的(大Q)還是寬的(小Q)。如前一節所述,用最佳可能曲線擬合未知電路的傳遞函數,可以了解電路的特性,從而確定其組成元件的值。
RCL和CLR配置
基本元件R、L和C的其它組合可以提供不同類型的濾波器。我們之前已經看到RLC配置是二階低通濾波器,但是如果我們在它們之間切換一些組件呢?圖5和圖6顯示了兩種新的配置,即RCL和CLR電路:
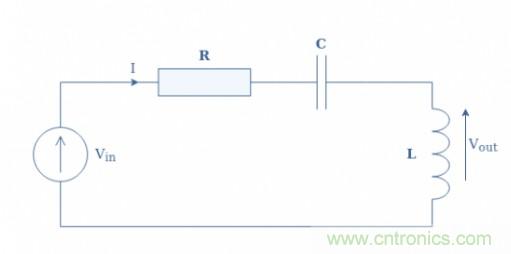
圖5:RCL電路示意圖
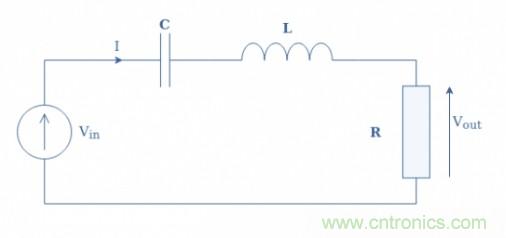
圖6:CLR電路示意圖
盡管這些電路和圖1中所示的原始RLC電路之間的變化很小,交流響應非常大不一樣。它可以證明這兩個電路的傳遞函數由等式4和5給出:
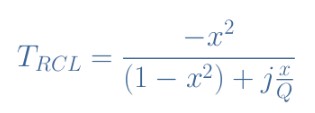
公式5:RCL電路傳遞函數
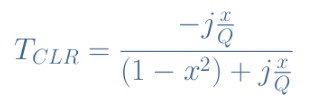
公式6:CLR電路傳遞函數
通過繪制具有相同值的傳遞函數范數:R=10Ω和20Ω,L=0.2h,C=100μF,揭示了這些新濾波器的性質。
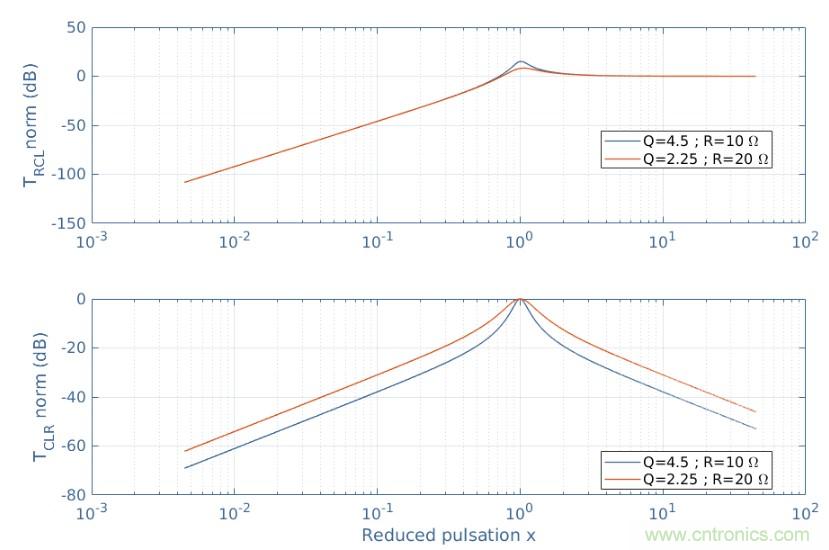
圖7:串聯RCL和CLR電路的增益
RCL電路是一種二階高通濾波器,因為它可以衰減ω0以下的頻率。電路CLR是一個帶通濾波器,因為它只放大ω0左右的頻率。請注意,與上一節中關于曲線形狀作為Q函數的注釋仍然適用于這兩個過濾器。
結論
串聯RLC電路是由三個基本電子元件串聯而成:電阻器、電感器和電容器。電阻的阻抗是實數,電感器和電容器的阻抗是純虛數,電路的總阻抗是這三個阻抗之和,因此是一個復數數字。那個第二節首先定義并給出電路的瞬態響應。它包括在高電壓階躍下研究電路的行為。通過研究與電路相關的二階微分方程的可能解,可能存在三種情況:
欠阻尼響應,信號向永久值Vin緩慢振蕩。
信號緩慢增加到永久值的過阻尼響應。
臨界阻尼響應是信號向永久值增長最快的情況。
第三部分介紹了電路的交流響應。當提供交流信號時,微分方程可以寫成復數形式,以便找到電路的傳遞函數。繪制該函數的范數表明串聯RLC電路具有二階低通特性過濾器。輸入最后一節研究了RCL和CLR兩種不同的結構。這一節說明,二階高通濾波器或帶通濾波器可以由同一電路通過簡單的開關元件來實現。
推薦閱讀:







