中心議題:
- 利用單相接地故障數據估計小電流系統對地電容電流的方法
解決方案:
- 用兩組發生在不同線路上的故障數據求該系統各線路的對地電容
系統電容電流是調度和運行單位要了解的系統參數之一,是設計單位選擇補償設備的依據,故研究該項工作具有重要意義。目前,電容電流的測量方法主要有單相金屬接地法、相對地附加電容法及中性點附加電容法。
采用單相金屬接地法,易造成兩相對地短路及鐵磁諧振過電壓,危險性較大。采用相對地附加電容法,其安全隱患主要發生在附加電容本身上,例如測量電纜線路時,附加電容一般放置在開關柜附近,在測量過程中附加電容如存在缺陷發生爆炸,可能危及其它配電柜,造成重大事故;另外在測量35kV系統電容電流時,因系統電壓較高,附加電容容量較大,有的試驗單位可能并不具備合適的電容器。采用中性點附加電容法,如在測量過程中系統出現單相接地,中性點電壓上升到相電壓,將危及運行人員及表的安全,而且測量誤差大。
在實際運行中,對于出線數較多、線路較長或包含大量電纜線路的配電系統,當其發生單相接地故障時,對地電容電流會相當大,接地電弧如果不能自熄滅,極易產生間隙性弧光接地過電壓或激發鐵磁諧振,持續時間長,影響面大,線路絕緣薄弱點往往還會發展成兩相短路事故。因此,DL/T620-1997《交流電氣裝置的過電壓保護和絕緣配合》規定:3~10KV鋼筋混凝土或金屬桿塔的架空線路構成的系統和所有35KV、66KV系統,當單相接地故障電流大于10A時應裝設消弧線圈;3~10KV電纜線路構成的系統,當單相接地故障電流大于30A,又需在接地故障條件下運行時,應采用消弧線圈接地方式。
消弧線圈一般為過補償運行(即流過消弧線圈的電感電流大于電容電流),這也就是說裝設的消弧線圈的電感必需根據對地電容電流的大小來確定,以防止中性點不接地系統發生單相接地而引起弧光過電壓。而實際情況是,現場運行人員對系統的接地電容電流值究竟有多大了解的并不詳實,或者是掌握的數據僅憑經驗而得,或者是數據過于陳舊,不足為憑。
所以,針對研究該問題的重要性以及以往方法的種種不利之處,本文提出一種利用單相接地故障數據估計小電流系統對地電容電流的新方法。
方法介紹
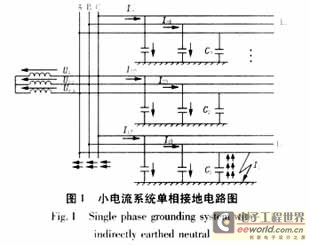
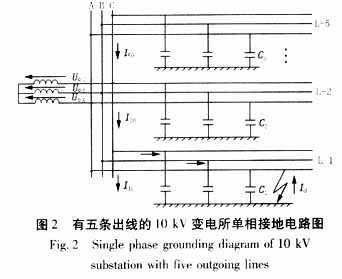
對于一個中性點絕緣系統,發生單相接地故障時的等值電路如圖1所示,由于配電網線路中各相對地的泄漏電導比線路對地電容的導納小得多,所以分析時忽略了泄漏電導,并認為三相對地電容相等。
接下來利用單相接地故障的零序電壓和零序電流數據來估計系統對地電容值,由于電流波形比較雜亂,利用公式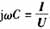 求電容不可避免的造成較大誤差,所以,本方法利用零序電壓和零序電流的瞬時值來求電容。由公式
求電容不可避免的造成較大誤差,所以,本方法利用零序電壓和零序電流的瞬時值來求電容。由公式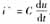 ,將其寫成離散化形式,為:
,將其寫成離散化形式,為:
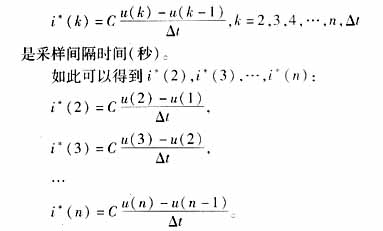
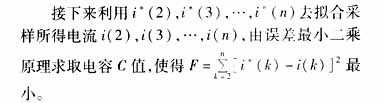
[page]
由于F的每一項[i*(k)-i(k)]2都可以展開成電容C的多項式:
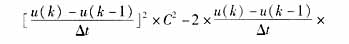

這樣,當系統的某一條出線i(i=1,2,...,n)發生單相接地故障時,利用系統零序電壓與故障線路零序電流可求出該系統除了故障線路以外的其它線路對地電容值之和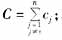 ;利用零序電壓與任一條非故障線路的零序電流可求出該非故障線路的對地電容值;并且,對同一次故障在數值上有
;利用零序電壓與任一條非故障線路的零序電流可求出該非故障線路的對地電容值;并且,對同一次故障在數值上有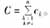 。對于長線路計算結果可認為準確,對于短線路,計算誤差稍大,可通過一些具體途徑改進,本文不作詳細敘述。
。對于長線路計算結果可認為準確,對于短線路,計算誤差稍大,可通過一些具體途徑改進,本文不作詳細敘述。
這樣,利用兩組發生在不同線路上的故障數據就可求出該系統中各線路的對地電容,且隨著故障次數的增多,還可利用多次的故障數據對系統對地電容進行修正。系統對地電容值求出后,由公式I=jωCU可以很容易就估計出系統電容電流的有效值,以此可以決定系統是否需要安裝消弧線圈以及消弧線圈電感值的大小。
EMTP仿真驗證
接下來對一個系統進行EMTP仿真,驗證該方法。系統為一個有五條出線的變電所, 基波頻率f=50Hz,采樣頻率fs=5000 Hz。仿真采用三相分布參數集中電阻線路模型,已知各出線長度分別為l1=l4=l5=10 km,l2=30 km,l3=6 km;線路參數分別為:R0=0.23 Ω/km,ωL0=1.72Ω/km,ωC0=4.175 μΩ/km;R1=0.17Ω/km,ωL1=0.28Ω/km,ωC1=5.715μΩ/km,當t=0.0075s時在第一條出線的A相線路中間發生單相金屬接地故障(見圖2)。取0~0.04秒的2個周波200個點的數據進行分析。
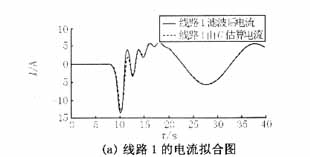
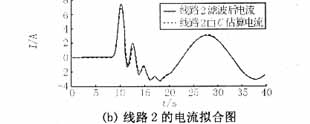
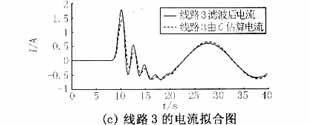
對上述方法用Matlab編程,對仿真數據進行分析,求解系統對地電容值。考慮到噪聲污染以及各種隨機干擾的存在,先對故障數據進行數字濾波,將17次以上的諧波去除后再對仿真或實測數據進行運算。本例所得由電容所計算電流與濾波后電流擬合波形如圖3所示(本文對數據濾波時采用的是巴特沃思濾波器,除去9次諧波以上的高次諧波)。
[page]
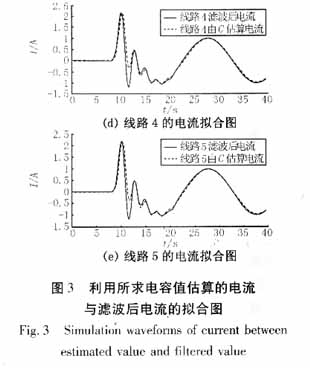
由零序電壓和故障線路零序電流求得的對地電容為:C∑=-0.75462μF,由零序電壓和非故障線路2、3、4、5的零序電流求得的電容分別為:

其中,C∑為負是因為故障線路零序電流和非故障線路零序電流反相的緣故。
由此可得:C2+C3+C4+C5=0.75462μF,可見其數值上與C∑相等。并且,由系統參數ωC0=4.175μS/km可推出C0=4.175/314=0.013296μF,則由Ci=C0*li可得:C2=0.39888μF,C3=0.07978μF,C4=0.13296μF,C5=0.13296μF,可見,這些值和利用本方法估計出的各線路對地電容值差甚微。
利用該方法對同一系統進行EMTP仿真,進一步驗正該方法。t=0.0075s時在第一條出線的A相線路中間發生單相電阻性接地,接地電阻100Ω,同樣取0-0.04s的2個周波200個點的數據進行。
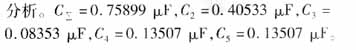
結論
傳統測量電容電流的方法可分為直接法和間接法兩種:直接法是使線路接地,直接測量接地電容電流,此方法操作及接線復雜,而且有可能危及非接地相絕緣薄弱處的絕緣造成兩相異地短路,對操作人員與配電系統都不安全,因而一般很少采用。目前廣泛采用的是間接法,即,在線路上外加一個電容,測量電壓的變化,從而間接計算出電容電流值。這種方法雖能較準確地測量電容電流值,但測量時仍需與一次側打交道,人員與設備安全仍得不到保證。另外,由于要涉及一次設備,因此操作繁瑣,準備工作時間長,工作效率低,通常大部分時間耗費在等待調度命令、開工作票、倒閘操作及安全措施準備上,工作效率非常低。
本文介紹的方法,簡單易行,僅僅利用系統單相接地時的故障數據進行計算,不必利用儀器進行現場實地測量,不影響電網正常運行,免除了麻煩且避免了危險。該方法適用于對誤差要求不很嚴格并且工作量較大的場合,經過仿真表明,結果較為準確。








