【導(dǎo)讀】 運(yùn)算放大器從有限增益單極放大器近似為無限增益單極運(yùn)算放大器,推導(dǎo)出跨阻放大器電路的增益,如圖1所示。
運(yùn)算放大器從有限增益單極放大器近似為無限增益單極運(yùn)算放大器,推導(dǎo)出跨阻放大器電路的增益,如圖1所示。
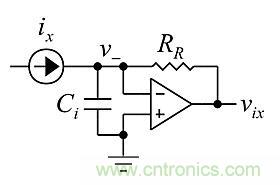
圖1:一個(gè)看似簡(jiǎn)單的電路只有兩個(gè)器件:運(yùn)算放大器和反饋電阻。
從第一部分得知,推導(dǎo)增益即跨阻抗為:
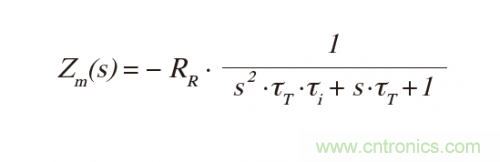
極點(diǎn)是:
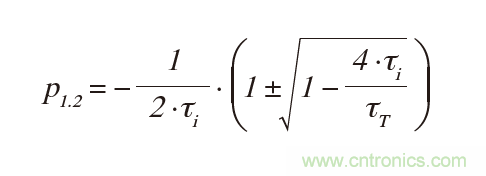
放大器增益使我們有機(jī)會(huì)將控制理論應(yīng)用于電路。這個(gè)例子將說明控制理論在理解電路動(dòng)態(tài)特性時(shí)的重要性和實(shí)用性。逐步實(shí)施,而不是一股腦全堆進(jìn)來,希望這樣能夠?qū)刂萍夹g(shù)及其應(yīng)用方式有深入了解。
極點(diǎn)對(duì)(二次)多項(xiàng)式通常表示為:
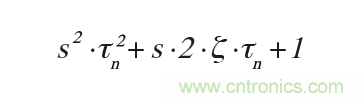
放大器的諧振時(shí)間常數(shù)τn = 1/ωn = 1/(2 x π x fn)和阻尼ζ分別為:
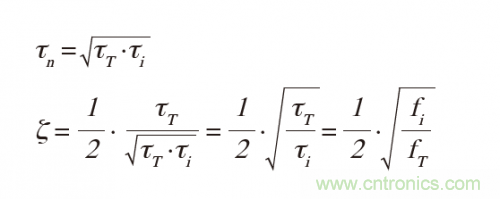
當(dāng)ζ<1時(shí),極點(diǎn)變?yōu)閺?fù)數(shù)極點(diǎn)對(duì),極角為:
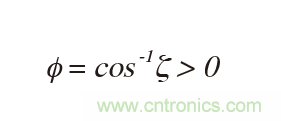
對(duì)于實(shí)極點(diǎn),ζ > 1且φ = 0。
對(duì)于恒定組(或包絡(luò))時(shí)延(最大平坦包絡(luò)延遲/MFED或貝塞爾)響應(yīng),相位隨頻率線性減小,并且發(fā)生在φ = 30o的極角處。所有頻率的時(shí)延都是相同的,保持波形不變。然后:
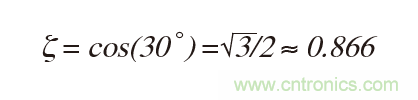
對(duì)于跨阻放大器MFED響應(yīng):
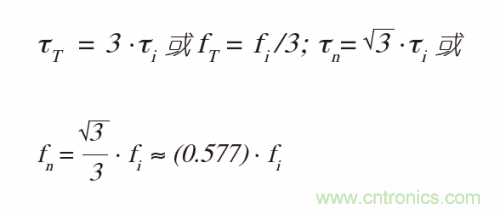
對(duì)于臨界阻尼(沒有過沖的最快階躍響應(yīng)),ζ = 1且τT = 4 x τi或fT = fi/4。兩個(gè)極點(diǎn)都是fi/2。
隨著RR變大、fi減小,放大器在vix中顯示出更大的過沖。在某種程度上,這對(duì)于Z-meter是有利的,因?yàn)闃O角φ = 45°,阻尼ζ = cos(φ) = cos(45o) ≈ 0.707,并且頻率(或幅度)響應(yīng)是恒定或平坦的,接近帶寬頻率。這就是最大平坦幅度(MFA)頻率響應(yīng)。對(duì)于穩(wěn)態(tài)(頻域)應(yīng)用,MFA響應(yīng)是最佳的。對(duì)于具有理想階躍響應(yīng)的瞬態(tài)(時(shí)域)應(yīng)用,MFED響應(yīng)是最佳的。(在示波器垂直放大器的設(shè)計(jì)中,優(yōu)化兩種響應(yīng)的標(biāo)準(zhǔn)是沖突的。)
運(yùn)放速度和放大器穩(wěn)定性
慢運(yùn)放具有低fT且τT >> τi,導(dǎo)致兩個(gè)實(shí)極點(diǎn)離得比較遠(yuǎn)。在極限值:
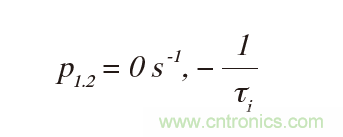
這是原點(diǎn)和fi處的極點(diǎn)。fT必須足夠小以保持fT << fi。然而,隨著fT減小,環(huán)路增益減少,可能不足以維持容許的運(yùn)算放大器增益誤差。在這種情況下,精度需要一定的速度。
隨著運(yùn)放fT的增加,Zm的阻尼減小,穩(wěn)定性降低。對(duì)于給定的ς和fi:
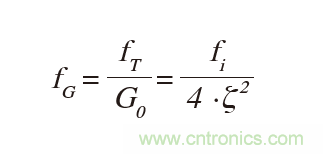
若fT = 1MHz且G0 = 105,則fG = 10Hz,并且臨界阻尼回路(ζ = 1)的fi = 40Hz。假設(shè)Ci = 10pF,那么RR = 398MΩ,這樣對(duì)于任何較小的值都可以保持fi > 40Hz。
圖2顯示了閉環(huán)極點(diǎn)隨著fT(更快的運(yùn)放)的增加而移動(dòng)的情況。在原點(diǎn)和fi(–1/τi)處的分離極點(diǎn)在fi/2(此時(shí)π = 1)處聚集在一起,然后變?yōu)閺?fù)數(shù)極點(diǎn)對(duì)。隨著fT增加,極角增加并且ζ減小。放大器變得不穩(wěn)定,響應(yīng)更加振蕩。
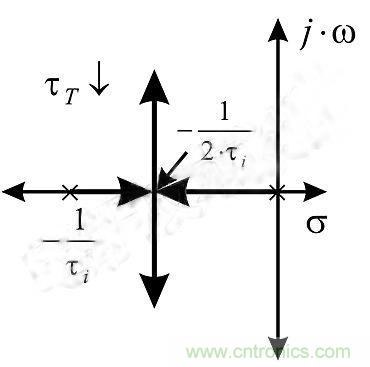
圖2:閉環(huán)極點(diǎn)隨著fT的增加而移動(dòng)。
只要變化的參數(shù)(圖2中的fT或τT)同時(shí)出現(xiàn)在多項(xiàng)式的s2和s項(xiàng)中,圖中就會(huì)顯示極點(diǎn)移動(dòng)的位置或軌跡。放大器在無限fT時(shí)阻尼最小,當(dāng)τT → 0s時(shí)極點(diǎn)位置在極限值:
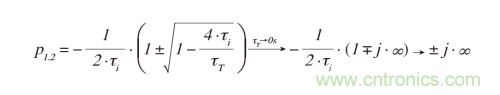
在jxω軸上有兩個(gè)值,其響應(yīng)是穩(wěn)定的(而不是振蕩的):原點(diǎn)和±jx ∞處。兩者都是無限的,(Zero(0)是無窮小的)。當(dāng)τT → 0s時(shí),極點(diǎn)多項(xiàng)式的s中的兩個(gè)項(xiàng)接近零,留下恒定的1項(xiàng),并且不受頻率影響。在極限情況下,極點(diǎn)位于jxω軸上,ζ= 0(振蕩器的條件),但在s的有限值處,它們的幅度為零。極點(diǎn)頻率很高,阻尼不再重要。它們與fi相距太遠(yuǎn)而不會(huì)影響環(huán)路動(dòng)態(tài)。這是理想運(yùn)算放大器的條件。因此,我們可以得出結(jié)論,對(duì)于非常慢或非常快的運(yùn)算放大器,極點(diǎn)是充分分離的,以使響應(yīng)穩(wěn)定。只有在fT的范圍內(nèi),這時(shí)運(yùn)算放大器和Ci極點(diǎn)太靠近,阻尼在足夠低的極點(diǎn)頻率fn處過度降低,同時(shí)放大器中發(fā)生幅度相當(dāng)大的振蕩。
再回到跨阻放大器,如果運(yùn)算放大器幾乎是理想的,也就是說,速度快到τT ≈ 0s,則極點(diǎn)多項(xiàng)式大約為1。對(duì)于足夠快的運(yùn)算放大器,fT >> fi,而且極點(diǎn)分開,就會(huì)有穩(wěn)定的環(huán)路。為了提供額外的阻尼,使運(yùn)算放大器fT(和環(huán)路增益)不會(huì)過低,電容器Cf需要通過RR分流。然后用包含Cf的電路代數(shù)計(jì)算:
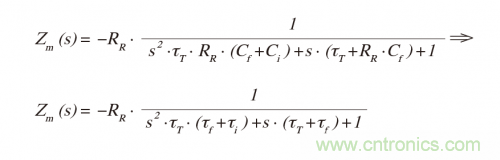
極點(diǎn)對(duì)參數(shù)為:
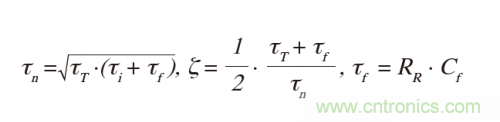
Cf的作用是在二次系數(shù)中將τf加到τi,更重要的是加到線性項(xiàng)中的τT,這會(huì)增加阻尼。因?yàn)?tau;i = τT,所以:
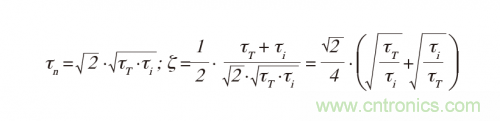
對(duì)于臨界阻尼,設(shè)π = 1;那么τT = (3 + 2 x √2) x τi ≈ 3.414 x τi且τn ≈ 1.848 x τi。如果沒有Cf(Cf = 0pF),如先前所計(jì)算的,τT = 4 x τi。若有Cf,在相同的動(dòng)態(tài)響應(yīng)下,運(yùn)算放大器可以更快,即具有更高的G0并實(shí)現(xiàn)更高的精度。
頻率響應(yīng)幅度和相位是:
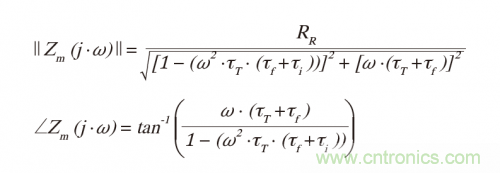
對(duì)于理想的快速運(yùn)算放大器(τT = 0s)并且當(dāng)Cf = Ci(τf = τi)時(shí),在頻率fg(或ωg)處具有響應(yīng):
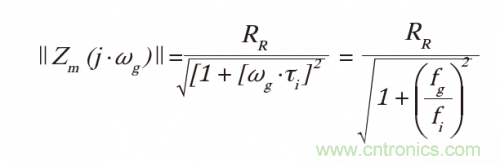
如果fi = 10 x fg,那么幅度誤差≈0.5%。因?yàn)閒i = 10 x fg,相位誤差 ≈ 6o。相位誤差對(duì)頻率效應(yīng)比對(duì)幅度誤差更敏感。這在阻抗計(jì)電路設(shè)計(jì)中很重要,有時(shí)在光電探測(cè)放大器中也很重要,因?yàn)楣怆娞綔y(cè)波形要與一些其它波形同步。
避免大反饋電阻的電路
對(duì)于一些帶跨阻放大器的Z-meter(ZM)設(shè)計(jì),RR要足夠大,即10MΩ或更大。當(dāng)RR變得非常大時(shí),要得到期望的阻尼,分流Cf必須很小,并且電阻分流寄生電容還可能過大。為了避免這個(gè)問題,可以使用以下電路代替。
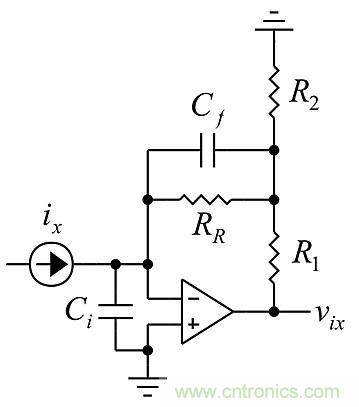
圖3:使用該電路避免電阻分流寄生電容過大。
要讓運(yùn)算放大器成為高增益單極運(yùn)算放大器,G ≈ –1/s x τT(參見本系列文章第一部分有關(guān)G的推導(dǎo))。反饋分頻器傳遞函數(shù)是:
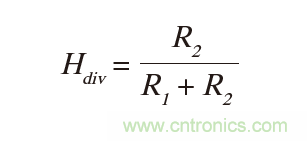
且τf = RR x Cf。當(dāng)電路用Rp = R1||R2求解時(shí):
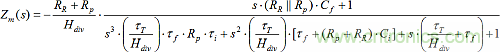
理想運(yùn)算放大器(τT = 0s)的Zm降低到:
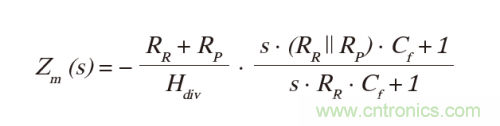
對(duì)于Rp = 0Ω,跨阻進(jìn)一步降低至:
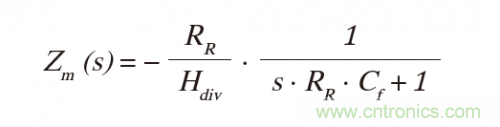
如果在輸出與RR和Cf之間插入快速×1緩沖放大器,則R1和R2分壓器輸出電阻不需要太小(Rp << RR)。那么當(dāng)Rp = 0Ω且運(yùn)算放大器具有τT時(shí):
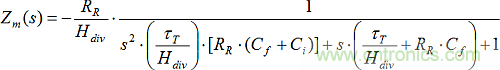
該電路與沒有輸出分頻器的情況有兩個(gè)不同:RR和τT都有效地增加了1/Hdiv。
結(jié)語(yǔ)
通過本文兩部分的闡述可以看出,即使是只有兩個(gè)器件的簡(jiǎn)單電路也可能涉及復(fù)雜的動(dòng)態(tài)推導(dǎo)。設(shè)計(jì)人員有時(shí)會(huì)避免使用這些推導(dǎo)來減少數(shù)學(xué)計(jì)算的麻煩,但是使用這些公式可以更好地了解給定電路在各種條件下的性能表現(xiàn)。我們介紹的跨阻放大器分析可為這樣的電路設(shè)計(jì)提供一個(gè)模板,并提供如何分析放大器動(dòng)態(tài)特性的指導(dǎo)性示例。
不要因?yàn)榱⒎交蚋叽味囗?xiàng)式而拒絕使用s域代數(shù)來解決電路動(dòng)態(tài)問題。我們?cè)诒緦?shí)例中遇到了一個(gè)立方項(xiàng),但沒必要去解它,因?yàn)橥ㄟ^簡(jiǎn)化可將多項(xiàng)式降為二次方程,方便以后的分析計(jì)算。這種情況很常見,因?yàn)殡娐吩谠O(shè)計(jì)階段常常被模塊化,它們要么彼此隔離,要么通過受控端口阻抗進(jìn)行受控交互。設(shè)計(jì)中可以應(yīng)用模板方案,但通常限于s域中的二次方程。
瑞芯微電子與OPPO簽訂VOOC閃充專利許可協(xié)議
高頻PCB電路設(shè)計(jì)常見的66個(gè)問題
淺析電阻分壓采樣電路
詳解功率MOS管的五種損壞模式
詳解三大常見電路保護(hù)器件






