【導讀】文中將詳細地為大家分析如下看點:幾個簡單的實例測驗與分析,共模電感“Z”字形符號解釋,共模電感是否會飽和,共模和差模的概念,共模電感設計的幾個經驗以及一些重要的基本概念。
看點1 幾個簡單的實例測驗與分析!
01 這是一個共模電感,如下測量,你覺得測得的電感量是多少?
可能有一部分會答錯。
下面來說明一下
我們知道共模電感的繞法有兩種,1 雙線并繞,2 兩組線圈分開繞。
1 雙線并繞

2 兩組線圈分開繞

正確的答案應該是10mH,下圖所示。一樓所示的測量和如下測量一致。如仍有懷疑,可找個電感測量一下便知。
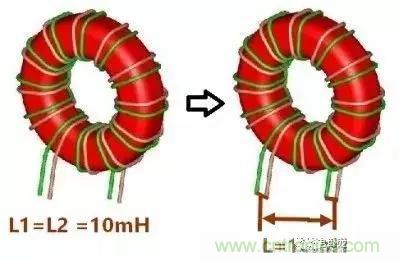
可以理解成兩個電感并聯,事實上就是兩個電感并聯,計算結果和測量結果是一樣的。

兩種繞法有何特點?
1 雙線并繞
有較小的差模電感
有較高的耦合電容
有較小的漏感
2 兩組線圈分開繞
有較小的耦合電容
有較高的漏感
因此要根據實際應用情況選擇繞法。
02 再看看這樣測量出來的電感量是多少?為什么?
有的人可能會回答0mH,有的人可能會回答20mH,有的人可能會回答10mH。
不過很遺憾都不是,正確的答案L=40mH。如下圖,按右手法則已標上電流方向和磁通方向,從圖中可以看出兩個線圈的磁通的方向是相同的,也就是說磁通是增加的不是相互抵消。
根據磁環電感量計算公式
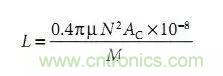
式中:N = 圈數, Ac = 截面積, 分母 Mpl = 磁路長度。
注意 N 有平方的,一組線圈的圈數是N, 則兩組線圈的圈數是 2N,將2N代入到公式中分子有 4N², 也就是說電感量為 4 倍。本例則為 40 mH。
03 再看看這樣測量得到的電感量應該是多少?這樣測得的是什么電感量?
這個估計很多人都知道是0mH,沒錯,理想狀態下就是 0mH。
實際共模電感總有漏感、或差模電感成份,因此按此連接測量得到的數值就是漏感或者叫差模電感。
共模電感中漏感和差模電感是一回事,可以稱漏感也可稱差模電感。一般做得好點的漏感在1-2%左右。
但有時候會特意將差模電感和共模電感做在一起,這時候的差模電感量就按實際需要做了。
看點2 共模電感“Z”字形符號是代表什么?
共模電感的這個符號應該很常見吧,但是符號中的的 “Z” 一樣的符號該怎么讀?估計很少有人知道。
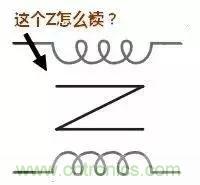
Z= Zorro (佐羅),很厲害的一個人物。共模電感也叫 Zorro 電感。英文中共模電感的叫法比較長 Common Mode Choke,或 Common Mode Inductor,也稱 Zerro Inductor,有時簡稱為 Zerro。
舉例: Fairchild 的 關于濾波器的文章中也是這么用的,如圖:
看點3 共模電感會飽和嗎?
共模電感會飽和嗎?答案是非常難飽和,通常情況下無需擔心飽和問題,為什么呢?我們先來看看差模電流流過共模電感的情況。如圖,差模電流電流電感時其磁通是相互抵消的,也就是說,在磁路里基本沒有磁通產生,差模電流流過時沒有阻力,沒有損耗,簡單說,一個額定電流5A的共模電感流過100A的差模電流也不會飽和,當然前提是導線夠粗。
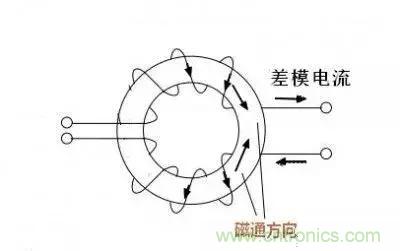
共模電流的情況相對復雜一點,百度了一下發覺都是抄來抄去,都是籠統的說阻抗增加,但并沒有說明為何阻抗增加,基本沒什么參考價值。
我們按如下方法分析一下:
假設一對共模電流流向如下圖所示,兩個濾波電感各自獨立,沒有磁通上的聯系,這樣能不能濾波共模電流呢?當然也能,相當于差模電感,各自為戰,效果差一點。
于是我們講兩個電感合二為一,如圖,這樣會發生什么情況呢?
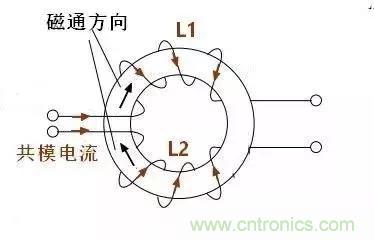
顯然,流過L1的共模電流和流過L2的共模電流產生磁通相互疊加,總磁通增加。L1和L2除了自感以外還有互感,L1的電感量除了本身的電感外還要加上L2的互感,反之L2也一樣。
這樣情況又要分幾種:
1)L1的磁通會使L2產生互感電動勢,互感電動勢的方向總是要阻礙磁通的增加,于是在L2中產生和共模電流方向相反的電流,L2的共模電流被抵消,反之,L1對L2的互感電流也是與L1的共模電流方向相反,也就是說L1的共模電流被抵消。如下圖所示,L2中的互感電流與L2的共模電流方向相反的:
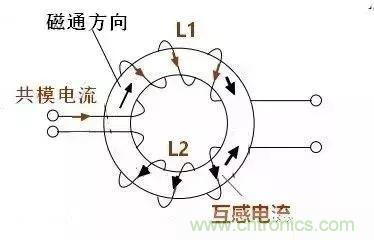
2)電感量計算,如圖:
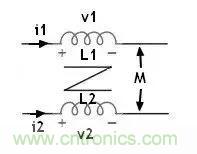
根據自感公式:
則L1的有效電感為:
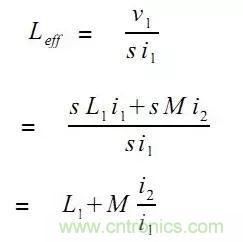
設:
于是有:
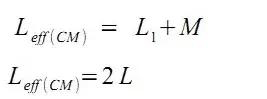
即共模電感量為繞組的兩倍。
對于差模電流有:
于是,差模電感
即:
也就是說差模電感量為0。
看點4 共模和差模的概念
共模和差模的概念:這個很好理解,看一下圖便知。
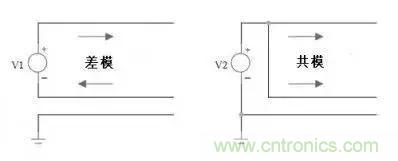
共模干擾來之何處?共模干擾的頻率如何?1MHz以上還是5MHz以上?如圖:
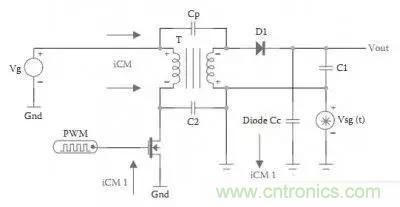
共模干擾由MOS管的高di/dt引起,經過變壓器間的電容Cp或雜散電容C2傳到副邊,以Cp為主,C2基本可忽略。我們知道Cp很小,因此能傳到副邊的干擾頻率一定很高,低頻干擾信號過不去,因此EMI測試中的高頻部分基本就是共模干擾。究竟多少MHz與變壓器的結構有很大的關系,層間電容大了則可能1MHz的共模能過去,層間電容小了,則只能是更高的頻率能過去,比如5MHz以上。
由此可見,變壓器的繞制對EMI有不可忽略的作用,并且需要在漏感和繞組電容中折中考慮,漏感小了則初次級的電容一定大了,初次級的電容小了則漏感大了,初次級電容小則有利于抑制共模干擾,但漏感大了會在給原邊的MOS管帶來壓力。
如何既能減小原付邊電容又保持漏感小呢,目前看來=只有一個辦法,在原付邊件加屏蔽。簡單說,在原邊和付邊之間一圈不到的銅箔,銅箔不可繞滿,不可重疊,留1mm左后的空隙。實測效果不錯的,但變壓器繞制就復雜了。
我們來認識一種新的電容,其實也不是新的只不過估計很少有人知道,很少有人用。
如圖,稱為 Feedthrough 電容,專門用于EMI抑制電路,其抑制高頻干擾效果相當好。

其內部等效結構如圖
其在電路中的符號為:
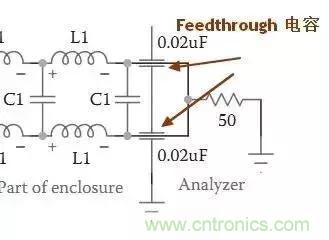
其特點為,低ESR,低ESL,高諧振頻率,因此專用于EMI抑制。
其參數等詳細資料可網上搜索廠家的說明書。
以下的圖應足夠能說說明這個電容。
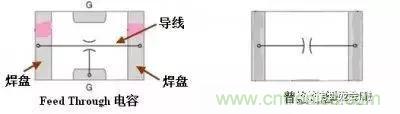
從上面的做圖可以看出這種電容的內部其實是導線(實際有電感),導線外面通過做成電容形式,并把電容一端接地,因此低頻或直流信號完全不受阻,但高頻則會通過電容接地。由于該電容沒有引腳,因此ESL(等效串聯電感)很小,這個至關重要。
有必要說明一下為什么電容的諧振頻率要高。
如圖,所有電容的ESR和阻抗曲線都有相似形狀,只是ESR或諧振點的位置不一樣,圖中諧振點左面電容呈容性,即具有電容的特性。但是工作頻率高了以后,電容的容性越來越小,過了諧振點后,電容的容性便消失,于是電容變成了電感。可想而知,本來在電路里放了一個電容,結果變成了電感,那是什么后果?
認識一下典型的濾波電路,如圖所示:
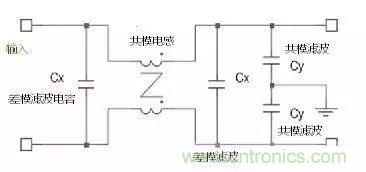
共模濾波器和差模濾波器對差模信號濾波效果對比,差模濾波器在濾出疊加在信號上的噪聲后導致波形失真。
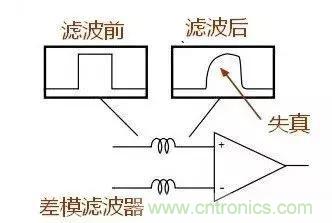
但使用共模濾波器濾出信號上的噪聲后波形沒有失真。
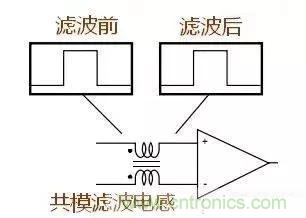
因此,對于數字信號如有噪聲需濾除采用共模濾波器比較合適。
說濾波器就不能不說濾波器的階數,談到濾波器我們可能會聽到或看到濾波器的階數,那么什么是濾波器的階數呢?我們看以下最簡單的RC濾波器,那是幾階?
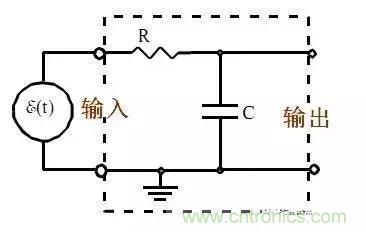
答案是:一階,英文叫 First Order
那這種呢?
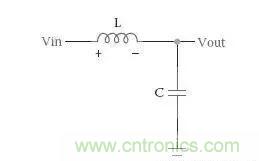
還有這種濾波器是幾階的呢?
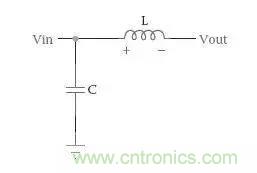
答案都是二階,英文叫 Second Order
這樣說應該明白什么是濾波器的階數了吧? 簡單講,有多少個儲能元件就是幾階,RC濾波器只有一個電容則是一階,LC濾波器有兩個儲能元件則是二階,與前后關系無關。
如下最常見的PI濾波器就是三階的了
那么一階、二階、三階濾波器性能上有何區別?
可以濾什么頻段是電感電容取值問題,但不同階數的濾波器還有更重要的特性,就是衰減信號的斜率問題。
我們先弄清十倍頻這個概念:
十倍頻,這個應該不難理解,從數軸上看,十倍頻就是頻率增加10倍,比如 2 到 20Hz 就是一個十倍頻,那么 50 到 5000Hz 是幾個十倍頻呢?
我們以一階和二階濾波器的衰減曲線為例,見圖
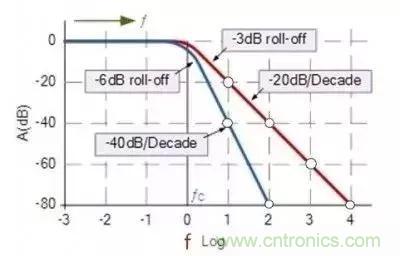
圖中橫坐標是頻率,用對數表示,縱坐標表示增益,單位為dB,注意圖中的圓點處,右面一條是一階濾波器的衰減曲線,圓點從1 到 2 頻率增加了十倍,從縱坐標中可以看到增益下降了20dB,通常稱為10倍頻程衰減20dB,左面一條曲線是二階濾波器,不難看出10倍頻程衰減40dB。
由此可知,濾波器每增加一階,十倍頻程衰減增加20dB,如下圖所示。
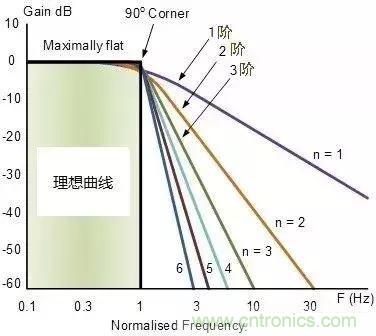
看點5 幾個疑問
小測驗:兩個電感,圈數一樣,直徑一樣,但繞制的長度不一樣,哪個電感量大?
小測驗:如圖,兩個電感圈數一樣,線圈高度一樣,直徑不一樣,哪個線圈電感量大?

線圈不同直徑 或 不同長度的形成的電感量參考以下截圖,式中 A 是線圈面積,l 是線圈高度,(注意不是磁芯的長度),按公式可以看出,面積越大電感量越大,線圈高度越小電感量越大。
需要注意的是,這個公式僅僅表示表示幾個量的相互關系,不能算出準確的電感量的。
如圖,一棒形電感(或工字形電感),在一端截去一部分磁芯,其電感量是增加了還是減小了?為什么?

問題:你買了一批工字磁芯(或磁棒)要加工成1mH的電感,需要繞多少圈如何計算?
工字磁芯或磁棒做電感算是算不準的,通常的做法就是試繞一定的圈數(比如繞一層)然后測量一下電感量,算出每圈的電感量然后再按此算出總的圈數,由于內圈和外圈的直徑不一樣每圈電感量也就不一樣,因此繞好后還得測量進行修正,有時廠家會給出有效磁導率,可參考,線圈在磁棒上的位置不一樣(靠近磁棒中心還是靠近兩端),疏密程度不一樣電感量均不一樣。
棒形電感有氣隙嗎?當然也有,棒形電感的氣隙就是端點到端點的距離,如圖所示棒形電感的氣隙是非常大的。
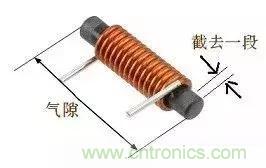
棒形電感的氣隙性質與磁環的氣隙性質有明顯不同,如圖,磁環開氣隙后其等效磁導率與沒有氣隙的磁環的磁導率相比小很多,氣隙越大等效磁導率越小,反過來說氣隙越小等效磁導率越大。

那么問題來了,磁棒截去一段后端與端的距離變短了,也就是氣隙變小了,但實際電感量也變小了,一種解釋是等效磁導率變小了,如圖所示。
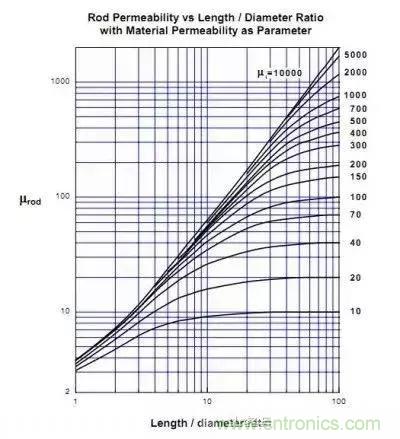
這個圖是被各種資料千萬遍引用的,屬于最經典的。這個曲線無非是實測以后得出的統計數據,并未道出問題的實質,而我們希望知道為何總得磁路短了電感量反而變小。
圖中橫坐標是磁棒的長度與直徑之比,隨長度變短氣隙變小等效磁導率也變小,這好像不合理,我們看磁環的電感計算公式:
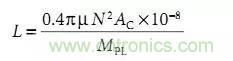
MPL表示磁路。
我們知道磁環的氣隙變小電感量會變大有效磁導率也變大。因此磁棒的氣隙變短了其等效磁導率應該變大并且電感量也應該變大才對啊,但事實相反,一定是哪里有問題了。
原因其實很簡單。真正的磁力線的密度其實是很高的,不像我們平時那么畫幾條意思意思的幾條。
可能這樣:
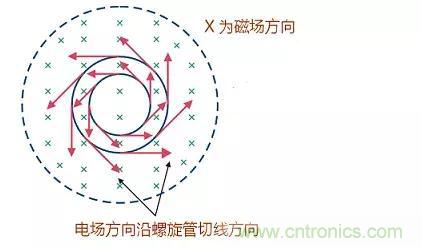
真正的原因是因為磁芯外部的磁場會在磁芯上產生感生電流,此電流方向與線圈電流反向相反,感生電流同樣會產生磁場,該磁場的方向與磁芯內原來的磁場方向相反,彼此互相抵消一部分,當磁棒被截短后,外部磁場增強,磁芯上的感應電流加大從而反向磁場增強,于是削弱了線圈產生的磁場,最終導致電感量減小。
看點6 共模電感設計的幾個經驗
共模電感的設計:共模電感設計很簡單,掌握以下步驟即可:
1) 盡可能選用磁導率高的磁芯以獲得最大的阻抗(對付30MHz以下的干擾MnZn,30MHz- 1 GHz用NiZn),
2) 選擇適合飽和磁通的磁芯,確保最大共模電流時磁芯不會飽和,(通常共模飽和電流只有3-5mA)
3) 選擇功率損耗小的磁芯
4) 在選定磁芯尺寸下繞盡可能多的圈數
5) 選用尺寸小的磁芯
6) 線間距盡可能大以減小雜散電容(避免高頻信號通過雜散電容耦合過去)
7) 由于繞線有電阻會發熱因此需要合適的線徑
電感的能量儲存在哪里?
這是個頗有爭議性的話題,我們通過以下實例來研究一下:
如圖是一個電源、一個開關、一個電阻和一個電感串聯在一起。初始狀態開關打開,電路中沒有電流。
現在我們將開關合上,會發生什么情況?這可以從兩個方面看:
1)電路理論:當一個電感中有變化的電流流過時電感兩端會產生感生電動勢(V = L di/dt),這樣電感中不但有電流還有電壓則其功率為 P= IV,既然有功率毫無疑問變化的電流帶來了能量。
2)物理學: 變化的磁場產生電場,而這個電場力則拼命將電子推回去,在推的過程中不斷獲取電子的能量,而電源則不斷給電子增加動能以通過電感,這樣電感電流不斷加大,電子的動能越來越強于是電場也越來越強。
隨著電流最后達到最大值1A,電感中的磁場不再變化,于是電感兩端電壓為0,(di = 0,V = L*di/dt = 0),于是電場強度也變為零(變化的磁場才會產生電場)。
隨后我們將電源電壓突然調為0V,結果會怎樣?
隨著電壓調到0,電子從電阻上流過能量逐漸在電阻上消耗掉,電流的變化再次建立起變化的磁場,而變化的磁場再次建立起電場,而此時的電場力給予電子能量并推動電子加速流出,隨著能量的耗盡,電流最后為零,磁場也逐漸消失。
如果在電流流動過程中我們突然打開開關,使電路呈開路狀態會發生什么情況?
電子正在有序的向前流動,此時開關突然斷開,于是所有電子不得不緊急停止,電流于是突然就變為零了,于是磁場瞬間崩潰,磁場崩潰過程中在電感兩端感應出極高的電壓(V = L*di/dt,dt趨于0),同時瞬間變化的磁場產生極強的電場,這強大的電場推動所有電子往前跑。不難想象這時在開關斷開處的電子的心里那個急啊:別擠別擠,再擠掉下去了,然而后面的電子不知道啊,在電場力的作用下如潮水般涌來,呵呵.
突然想起一句廣告詞叫做 “真的停不下來”。于是擠成一團的電子在強大的電場力下不得不一起沖出導線跑到空氣中,其電壓之高足以擊穿空氣(V = L*di/dt,dt趨于0),于是通過空氣向開關的另一端放電產生火花釋放能量或者看誰離得近不順眼的就向誰放電以釋放能量。
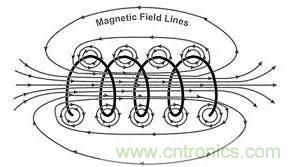
如圖是螺旋線圈中磁場和電場的關系示意圖,電場方向是沿線圈圓周的切線方向,而磁場在圖中是垂直穿過。
看點7 一些重要的基本概念
1 電磁場:電場和磁場總是聯系在一起的,電場和磁場的混合就是電磁場,英文也專門創建了這么一個單詞(Electromagnetic Field 電磁場),以下圖為例,
圖中是一小段PCB銅箔的截面,大小不斷變化的電流面向正面流進或流出,注意是變化的電流,因此產生了變化的磁場,由此也感應出電場,注意磁場的方向是環繞銅箔的,而電場是從銅箔指向參考面,參考面為地平面。磁場和電場這個方向特性要記住,在進行PCB布線線時為減小對其他電路的干擾可適當注意與磁場方向其他導線或電路成某種角度。
2分貝(Decibel):分貝是基于對數的單位,EMI測量中都用分貝作為基本單位的,因此對分貝需要有所了解。
分貝的基本定義:10log10[測得的功率/單位功率]
比如,測得5000mW,則10 log10[5000mW/1mW] = 37dBmW = 37dBm
注意通常 dBmW 是寫成 dBm 的,其W是省略不寫的。
如果用dBW作為單位,則37dBm = 7dBW,注意換算關系。
而實際EMC測量中都是測量的電壓或電流,通常是微伏或微安,最常見的就是 dBuV,這時候的坐標就不是10log了,而是20log,需注意。
這張表需要大致知道了解一點的
特別是表中三個框中的關系要知道,比如信號強度增加一倍則功率增加3dB,電壓或電流增加了6dB。仔細體會一下,信號增加10倍功率增加多少倍,電壓或電流增加多少倍。
3 電流的返回路徑,這是非常重要的概念:
3.1,低頻電流按最小電阻路徑返回,高頻信號從最小阻抗路徑返回,這是因為每一段導線都包含電感和電容。通常頻率以50KHz為分界線。
3.2,差模電流返回一定有路徑,你把路徑切斷差模電流就沒有了。
3.3,共模電流你一定要給它路徑,你不給路徑它就亂竄,造成嚴重的EMI問題。好似流氓,你給他一條生路他就比較太平,你不給他生路他就攪天下不太平。這也是為什么變壓器原邊和附件加Y電容給共模電流提供一條返回路徑。共模電流都是uA級或mA級,電流雖不大,但破壞力驚人。
3.4,差模電流返回路徑的包圍的面積一定要小,面經越大產生干擾信號越大,吸收外界的干擾也大。如圖所示
4 時域和頻域
時域是真實存在域,我們用示波器觀察到的波形就是典型的時域,所謂眼見為實。
頻域是一種數學構造,是假設用某種波形來構建不同的波形,通常是用正弦波,這不是我們這里要討論的問題。
而EMC測量都是采用頻域的方式,例如用頻譜儀或EMI接收器等。為什么要用頻域的方式測量EMC呢?我們知道,方波可有很多個(或無數個)正弦波構成,如下圖:
但每個正弦波的頻率額幅值是多少呢?用時域的方式測量很難,于是借助于頻譜儀,我們可測得每個波形的幅值及頻率,而這些頻率正是干擾頻率,稱為諧波,其幅值反映了干擾的強度。如圖所示:
再次強調:諧波的頻率是基波的整數倍。比如100KHz的矩形波,其諧波為300KHz、500KHz等。
5 三種無源器件的高頻等效模型
5.1,電阻的高頻等效模型
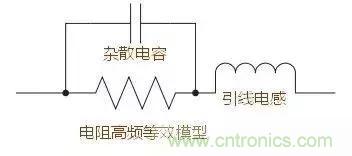
5.2電容的高頻等效模型
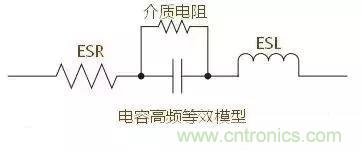
5.3,電感的高頻等效模型
6 近場和遠場
顧名思義,近場就是靠近電磁場,遠場就是遠離電磁場。
對PCB來說,電流回路一般以磁場為主,而大面積的金屬面(例如鋪銅、散熱器表面)以電場為主,或者說大電流的路徑上以磁場干擾為主而高壓部分則以電場干擾為主,或者說低阻抗路徑以磁場為主而高阻抗路徑以電場為主。因此有時大面積鋪銅散熱需要考慮該散熱面上是否有高壓,有高壓則會產生干擾電場。而大電流導線最好離敏感電路離得遠一點。(恒定電流不會產生干擾磁場,有干擾一定是有變化的電流引起)。至于電磁場強度則通常借助于近場探頭來進行測量。
7 電感的品質因素 Q
Q 是 Quality的第一個字母,電感的品質因素定義為:
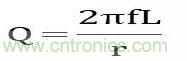
由上式可見品質因素是與頻率有關的量,在 r 不變的情況下,頻率越高則品質因素越高,然后通常我們不太使用Q這個量,而通常更關心的是Rdc,即電感的直流電阻,與電容類似,我們通常關心的是等效串聯電阻 ESR,而不是tgδ。電感線圈的直流電阻與電容的 ESR 一樣可通過電橋測得。
8如何數電感或變壓器的圈數?
問題看似很簡單,試試看如下線圈是幾圈?
9 近場探頭及探測原理
探測原理并不復雜,示意圖一看就明白

10 電感線圈的三種等效電路(忽略等效電阻)
電感線圈在低頻、諧振及工作頻率高于諧振頻率時會呈現不同的特性,特別是當工作頻率超過諧振頻率是電感不再是電感而變成的電容。圖中的電容是線圈的匝間電容。
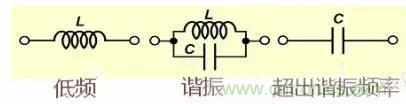
11 為什么MOS管腳上套個磁珠能起到抑制噪聲的作用?
雖然大家一直在這么用,但估計很少人會問為什么?我們先看看下面這張圖,這個磁環中間穿了根導線,你說這導線是饒了幾圈?

可能有人會說沒有繞啊,哪來的圈數?
事實上,導線穿過磁環就是饒了一圈,為什么呢?道理其實很簡單,這根導線如果沒有接入電路那確實是沒有繞,只要一接入電路就是一圈,它總要和電路構成回路,比如我們用電橋測量,如圖,這根導線就和電橋構成了回路,也就是形成了一圈。

MOS管腳上套個磁環后,MOS管的腳總是和外電路構成閉合回路,也就相當于MOS管腳在磁環上饒了一圈。由此可見,磁環的磁導率越高濾波效果越好。
12 插入損耗
如何評價一個濾波器的性能?通常采用插入損耗來評價。如圖示意圖表示信號 V1 --> V20,V20 表示沒有濾波器時的輸出。
為了對V1進行濾波于是插入了一個濾波器,將V1信號損耗在濾波器上,于是就有了這個名詞叫插入損耗。V2 表示插入濾波器后的輸出。

插入濾波后,會有什么結果?V2 一定小于 V20,也就是說插入濾波器后輸出變小了,為何輸出變小?一部分變成熱量、一部分被濾波器擋住返回了,如圖:
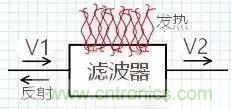
插入損耗按下式計算:
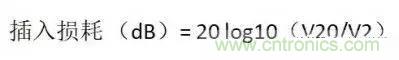
式中:V20為未加濾波器,V2 為加了濾波器。
13 傳導測試方法,
下圖是實驗室傳導測試的標準方法,建議各位花一分鐘時間看一下,了解實驗室是如何測試傳導干擾的,終身受用。
14 輸入端L C濾波器設計注意事項:
輸入端LC濾波器的一般形式如下:
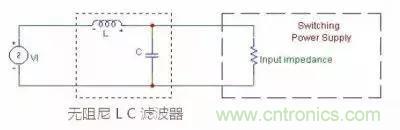
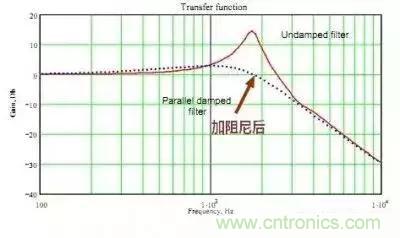
有于濾波電路中有兩個儲能原件因此是兩階濾波器,這濾波器有個很大的問題,由于無阻尼,因此當干擾信號的頻率達到濾波器的截止頻率時(Cut off),干擾信號不但沒有被抑制反而被放大了,如圖所示:
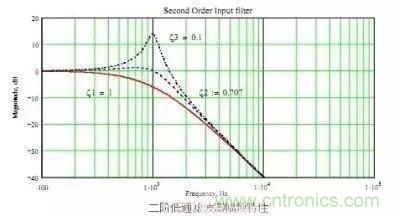
從圖中可以看到,當阻尼系數為0.1時,干擾頻率在 f0 處明顯被放大。阻尼為0.1時尚且被放大很多,沒有阻尼那更是不得了。
f0 = 1/2Π√LC, 為諧振頻率。
這可是事與愿違啊,我們本想抑制干擾但由于設計不當干擾非但沒有被抑制反而被放大了,這可不是我們所希望的。
當然,阻尼為零的情況是不存在,電感電容總有內阻,因此總有些阻尼作用的,但這遠遠不夠,而且不可控。通常采用以下幾種方法解決:
1)并聯阻尼法,如圖
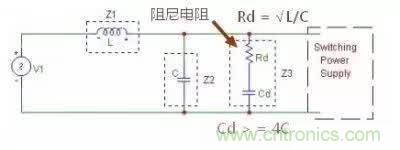
加阻尼后的幅頻特性
可以看出,截止頻率處的尖峰被壓平,也就是說不再使得噪聲被放大。其中電容 Cd 對阻尼不起作用,只是為了隔離輸入電壓以避免電阻產生
方法2:串聯阻尼法
如圖:在電感上并聯一個電阻與電感串聯的電路,這稱為串聯阻尼法,效果與并聯阻尼相同,不足之處是由于在原電感上并聯電阻電感后對高頻干擾信號的衰減差一點,這是顯而易見的。事實上大部分的實際應用中Ld 都被省略了,僅僅在電感上并聯一個電阻,這個電阻稱為阻尼電阻,目的與前述一樣防止在截止頻率處把干擾信號放大,實際使用中阻尼效果還是不錯的。
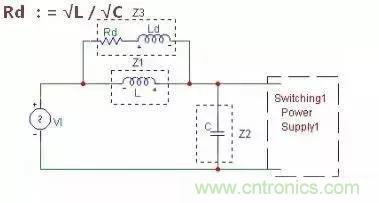
方法3:串并聯法:
這種方法用的人估計不多,了解一下即可,如圖:
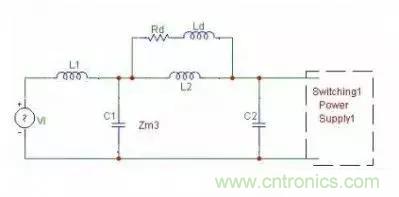
方法4,Π 濾波器
這是用的最多的一種,如圖,通常都僅僅在電感上并聯一個阻尼電阻,這個阻尼電阻不可少,曾經看到有些貼問這個電阻干什么用,有各種說法,但很少有說對的,請記住這個是阻尼電阻,為了消除干擾信號在濾波器的截止頻率處產生尖峰,達到243樓的的幅頻特性的加阻尼后的效果。有人說前面一個C1電容可以省去,這個說法不對的,我們前面已講過,每加一個儲能元件 L 或 C,濾波器的階數并升高一階,對信號的衰減可以增加20dB/十倍頻程,pi 濾波器是三級濾波器,把C1拿掉后變成了二階,濾波效果會打折扣。
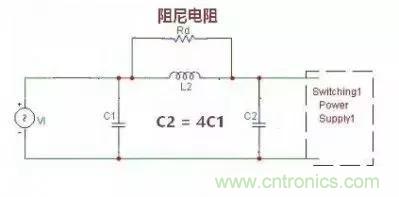
一個實例:
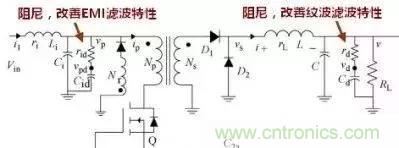
這是一個正激電源,請特別注意,輸入LC的EMI濾波器和輸出的紋波濾波器都有一個電容串聯電阻的阻尼電路,阻尼作用前面已多次提及。特別注意輸出端的阻尼電路,曾經見過帖子問為何在電解電容上串聯一個電阻,但似乎都沒有人知道為什么,請記住這是為了改善紋波性能加上的阻尼電路,有了這個阻尼電路課大大改善紋波性能。道理同EMI濾波器的阻尼相同。
15 共模電流會經過負載嗎?
答案是否定的,共模噪聲電流對用戶的負載其實沒什么影響,因為共模電流并不流過負載,如圖所示,由于共模電壓V3 = 0, 因此負載上并沒有共模電流流過,共模干擾信號只會以各種方式到 “地”。
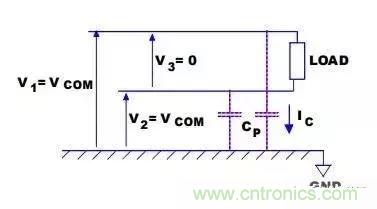
16 濾波器的Q值
Q = Quality,Q 是取 Quality 的第一個字母,是一個無量綱的值,濾波器的 Q 值是一個相當重要的值,理解及取適當的 Q 值 相當重要。
濾波器的 Q 值大小表明了能量在濾波器上損耗的大小,并且對濾波器的帶寬有很大的影響。Q 值越大能量損耗越小,這與電感的 Q 值一樣道理一樣,Q 值越大則能量損耗越小于是振蕩衰減越慢,這與反激原邊RCD吸收電路一樣,能量的損耗主要依賴電阻。
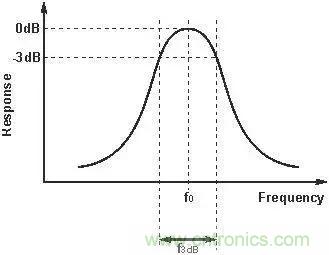
有些電路我們需要高 Q 值,比如振蕩器,Q 值越高越容易起振,比如收音機機調諧回路,Q 值越高選臺時越不容易串臺,這主要是 Q 值高時-3dB帶寬變狹的緣故。如下圖所示:
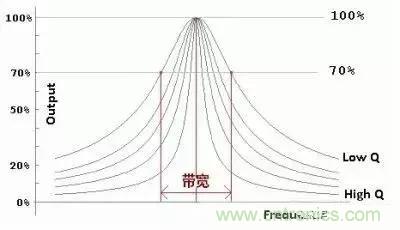
Q 值定義:
Q 值定義如下:
分子為存在與濾波上的能量
分母為每周期消耗的能量
或

意義如下:
Q 值得意義:
雖然是老生常談,但還是要再提一下:
Q< 1/2,,過阻尼。系統損耗很大,施加階躍脈沖后,系統沒有過沖并很快穩定下來。
Q > 1/2,欠阻尼。系統損耗很小,如果Q 率大于1/2,在階躍脈沖作用下,系統會有1次 到 2次的振蕩,隨 Q 值得增大,系統的振蕩次數會越來越多,理論上如果 Q 值無窮大,則系統將永遠在振蕩。
Q = 1/2,臨界阻尼。系統沒有過沖,在階躍脈沖作用下,會很快趨于穩定。
關鍵的問題是 Q 取多大為好?
答案是 Q = 5-10
答案是引用以下資料(在文章的結尾),文章不錯,對于設計LC濾波器及pi濾波器有參考價值,值得一讀。LC Resonant Circuits.
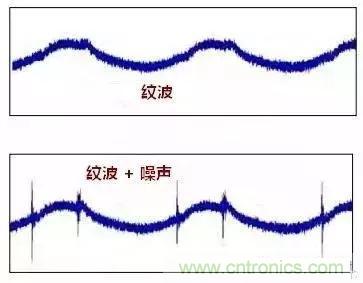
17 分清紋波和噪聲
常有人描述問題時把紋波和噪聲混為一談。紋波是低頻的,噪聲是疊加在紋波的干擾信號。如圖: