【導讀】噪聲傳導藉由導體傳導性和空間傳導性產生。在解釋導體傳導性的本質時,可能會運用傳輸理論概念。為便于理解以下內容,我們將用一種簡化的方法解釋EMC中用到的傳輸理論概念。
在傳輸理論中,導體被視為傳輸線路,電能在傳輸線上以波的形式傳導,并在末端發生反射。無論傳導的能量是信號還是噪聲,都同樣是以波的形式傳導的。因此,本章節首先針對信號先解釋了傳輸理論的概念,進而講述噪聲的傳導。
數字信號對脈沖波形的影響
(1) 反射導致諧振
當數字信號與10cm或更長的導線相連時,可能導致如圖1所示的振鈴現象。如上一章節所述,由于線路中存在電感和靜電容量,這可以解釋為諧 振。但是,根據傳輸理論,由于導線兩端信號波發生如圖2所示的反射,也可以認為導線本身作為一種諧振器,讓特定頻率成分變得非常明顯。這樣一來, 傳輸理論就從電波傳導和反射的角度解釋了這種現象。
運用傳輸理論可以預測,在振鈴的振蕩頻率處以及更高頻率范圍內會出現頻譜(圖中460MHz和860MHz)增加的現象(如圖1(c)所示)。
(2) 反射會干擾信號波形的傳輸
如果發生反射或諧振,脈沖波形無法正確傳輸。為正確傳輸信號波形,需要抑制導線兩端的反射。利用傳輸理論,可以提出一種抑制反射的設計,并預測反射導致的波形變化。
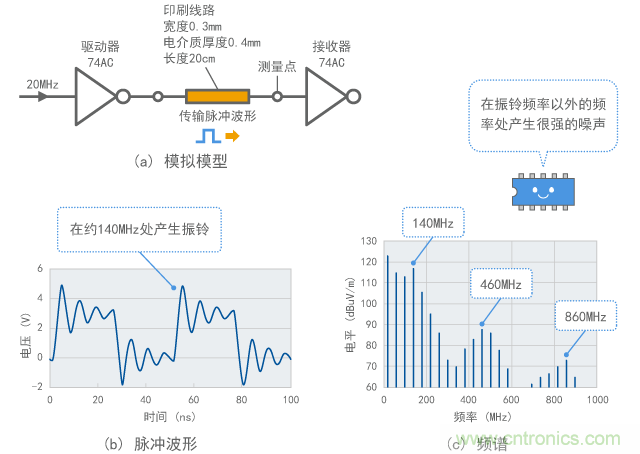
圖1 數字信號中振鈴的示例
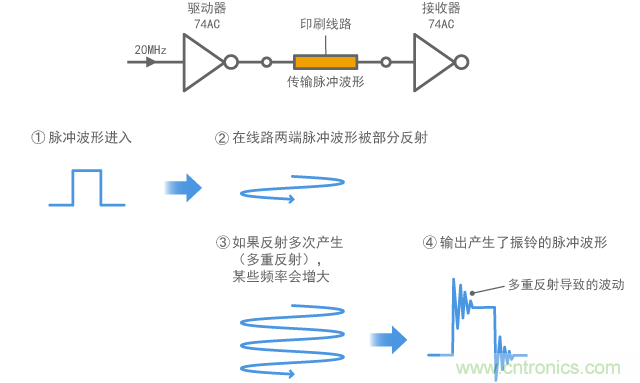
圖2 數字信號中產生振鈴的機制
[page]特性阻抗和反射
(1) 阻抗匹配
為抑制導線兩端的反射,需要執行“阻抗匹配”。“匹配”一詞指的是匹配導線的“特性阻抗”與連接至導線端的電路的“阻抗”。
(2) 特性阻抗
如圖3中信號線路所示傳導電波的導體被稱為信號線路。通過傳輸線路傳輸電時,電力和電流之間的比率恒定。這一比率就稱為特性阻抗。特性阻抗由每單位導線長度的電感和靜電容量決定(如圖3所示),是無損傳輸線路的純電阻。大家提到同軸電纜時說50Ω或75Ω,就是指的特性阻抗。如果本課程中沒有另作規定,我們則認為傳輸線路處于理想狀態而且沒有任何電阻損耗,以便簡化理論和表述。這也適用于后面的章節。(如果存在損耗,特性阻抗就不是純電阻,會使整個概念更加復雜。)
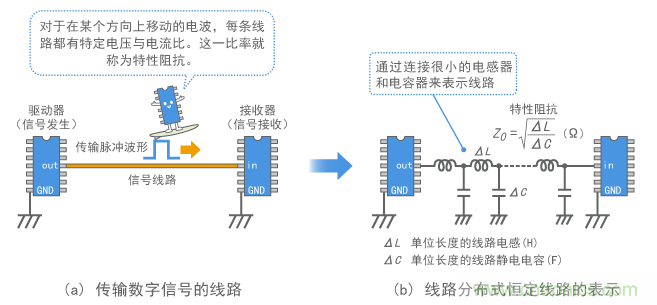
圖3 信號線的分布式恒定線路模型
(3) 負載、終端、終端匹配
如圖4(b)所示,當連接至導線端(以下稱為終端)的電路阻抗(以下稱為負載)與特性阻抗相等時,全部電能將被傳輸到負載,而不會發生任何反射。信號波形也被正確傳輸。在這種情況下,可以說此導線的終端是終端匹配的。
(4) 匹配能傳輸全部能量
如果導線端連接至另一個電路而不是負載,則電路的輸入阻抗會被視為負載阻抗,以考慮阻抗匹配。當電路的輸入阻抗與傳輸線的特性阻抗相同時,可以傳輸全部能量。在這種情況下,可以說這兩個電路相互匹配。
在噪聲抑制中,能量傳輸并不總是好事。在噪聲傳輸路徑與噪聲源或天線相互連接之處,形成較差的阻抗匹配更有利,這樣才不會傳輸噪聲能量。
(5) 反射波
如果負載阻抗不同于特性阻抗,信號能量會被部分反射,并通過傳輸線路逆流,如圖4(c)所示。這種波被稱為“反射波”,反射的大小以“反射系數”表示。如果發生反射,則會在終端處觀察到加入了輸入波和反射波的波形。
(6) 數字信號中包含的反射波
圖5提供了數字信號與傳輸線路和負載相連時所產生波形的一個示例。如圖5(a)所示,一根28cm長的導線(特性阻抗為50Ω)傳輸33MHz時鐘脈沖發生器信號。
圖5(b)給出了所連接負載具有與導線特性阻抗相同阻抗時的情形。脈沖波形被正確傳輸。(因為時鐘脈沖發生器的輸出電阻大,上升時間約為2ns。)
(7) 通過增加行波和反射波形成數字信號
圖5(c)給出了連接數字IC時的情形。信號振幅增加,同時可以觀察到一些過沖和下沖。觀察到的波形是由終端處產生的反射波和原信號右向行 波相重疊產生的。這就意味著終端處產生了具有與原信號相同跡象的反射波(圖4(c)),因此信號振幅看起來比原信號更大(圖5(b))。
與此相反,還存在另一種情形: 反射波的跡象與原信號相對,使信號振幅比原信號小。
表示反射波的這種跡象(更準確的說是相位)和大小的系數是反射系數。[page]
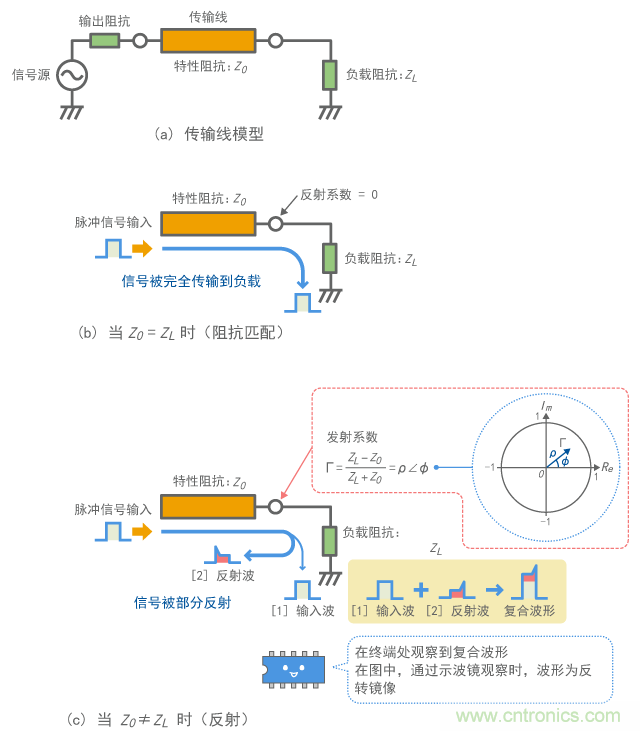
圖4 信號反射和匹配
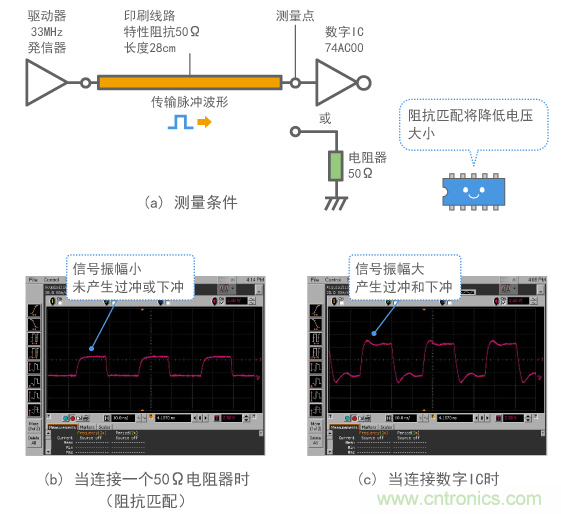
圖5 發生反射時數字信號波形的示例
(8) 反射系數是矢量
反射系數Γ是一個矢量,其大小為ρ,相位角度為Φ,可在復雜平面上標繪在半徑為1的圓內(如圖4(c))。因此,ρ的取值范圍為0到1。
ρ=1表示全反射,而ρ=0表示無反射。通常而言,該值隨頻率而變化。
隨著特性阻抗和負載阻抗之差變大,反射會越來越強,因此,ρ值增加(更接近圓的邊緣)。如果是完全反射,ρ等于1,標注在圓周上。
(9) 反射系數位于圓心意味著“匹配中”
在未發生反射時(匹配中時),反射系數被標繪在圓心處。按照前述方法通過圓內的位置來表示反射系數,會有助于從直觀上理解反射的狀態。史密斯圓圖就采用了這種方法。
另一方面,也可以根據特征阻抗和反射系數計算負載阻抗。
反射系數的概念也會用于后面講述的S參數。S參數是非常重要的概念,因為它們廣泛用于高頻波(并不局限于噪聲)的電子測量。
[page]數字電路阻抗匹配
(1) 數字信號特性阻抗
數字信號所使用信號線的特征阻抗有多大?如圖6所示,在以電源層和接地層為內層的4層電路板的表面有一根信號線,此信號線可以作為微帶線(以下稱為MSL)來處理,其中信號線的特性阻抗約為50Ω到150Ω。(如果有電源線,特性阻抗值可能更小。)
(2) 很多數字電路都未實現阻抗匹配
與此相反,數字IC的輸入阻抗通常一個幾pF的電容,在頻率為100MHz及以下時,會變成100Ω以上的高阻抗。因此,如圖7所示,數字電路的設計基本上會產生非常高的反射,從而導致在接收器處反射大部分信號能。
此外,數字IC驅動器側的輸出阻抗也會變化。因此,阻抗匹配并非總是在驅動器側完成,而且也可能導致反射。所以,數字信號一般會在信號線兩端造成反射(如圖2所示),而且會在造成多重反射一定程度時被傳輸。
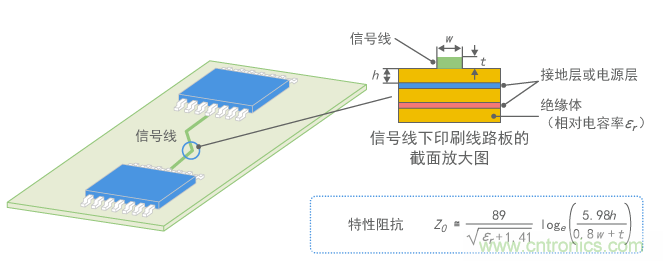
圖6 信號線的特性阻抗
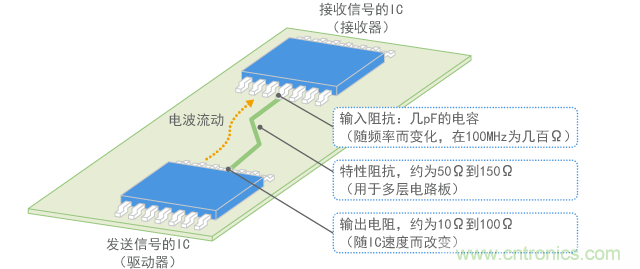
圖7 數字信號線的阻抗匹配狀態
(3) 駐波指示匹配狀態
盡管為了便于解釋在圖4中分別描述了輸入波和反射波,但在正常測量中很難單獨觀察這兩種波形(因為示波鏡只會顯示復合波形)。因此,可以按照后面的講述,通過觀察駐波來確定反射狀態。
如果因驅動器側和接收器側的反射而產生多重反射,傳輸線會形成一種諧振器,使某個特定的頻率變得特別明顯。從正確傳輸數字信號波形(即“信號完整性”)的 角度而言,傳輸線產生的諧振并不可取,因為它會導致振鈴。此外,從EMC的角度來看,這也是不可取的,因為它會在諧振頻率處增加噪聲。為抑制傳輸線產生的 諧振,導線的兩端或者一端應該靠近匹配狀態,以便吸收反射。
[page]駐波
(1) 電壓和電流隨測量點變化
在一定頻率處測量信號線上的噪聲時,如果終端處產生反射,就會觀察到如圖8所示的駐波。在這種現象中,您會發現由于“入射波”(原信號)和反射波之間發生干擾,不同位置的信號長度會有所不同。這種駐波是傳輸線路復雜狀況的根本原因,這將在后面進行描述。
如圖9所示,駐波較強處稱為“波腹”,而較弱處稱為“波節”。波腹和波節的位置隨頻率而有所不同。就其本質而言,電壓的波腹位置會成為電流的波節,而電壓的波節位置會成為電流的波腹。
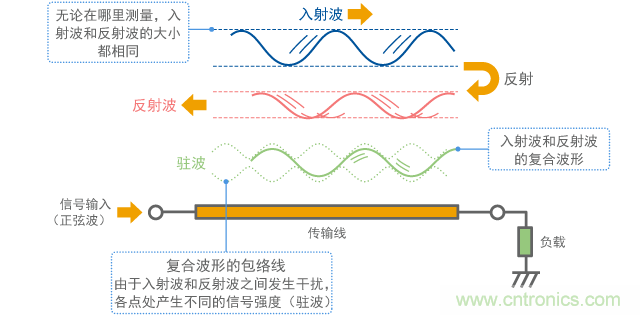
圖8 駐波
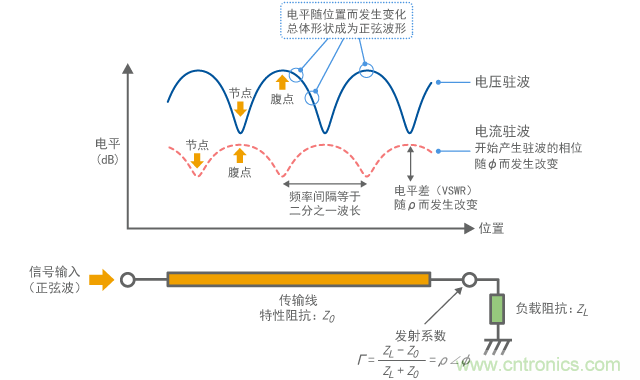
圖9 電壓駐波和電流駐波
(2) 觀察數字信號中包含的駐波
圖10到12提供了觀察如圖5所示數字信號波形的駐波的示例。在此,28cm長的信號線連接至33MHz時鐘脈沖信號,以 便觀察信號線周圍的磁場和電場。磁場和電場分別對應電流和電壓。觀察的頻率為490MHz(33MHz時鐘脈沖頻率的第15次諧波),測量間隔為5mm。
在各圖中,(a)的信號線右端有一個50Ω電阻器,以便近似得到阻抗匹配的狀態,而(b)中有數字IC輸入終端。
(3) 電流駐波
圖11給出了磁場的測量結果。盡管(a)(有阻抗匹配的終端)顯示傳輸線上具有恒定的磁場,(b)卻指出了不同位置處的強磁場(紅色)和弱磁場(藍色)。這就意味著紅色部分具有較大的電流。這被稱為駐波,其中較高反射系數ρ會導致最大值和最小值之差更大。
(4) 電壓駐波
圖12給出了電場的測量結果。與電流的情形一樣,(b)中使用數字IC作為負載,指示了不同位置處的變化。對比圖11和圖12會發現,就產生較強噪聲的位置而言,電壓和電流的情況正好相反(如圖9所示)。
如果產生了駐波,噪聲電平可能會隨不同位置而變化。因此,不能只通過某個位置測得的單個結果確定噪聲強度。[page]
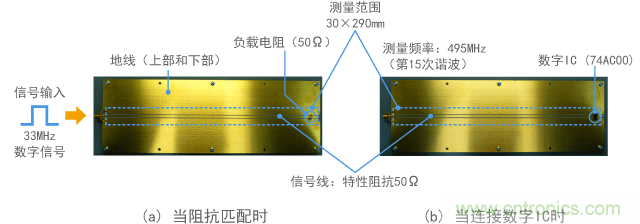
圖10 駐波的測量范圍
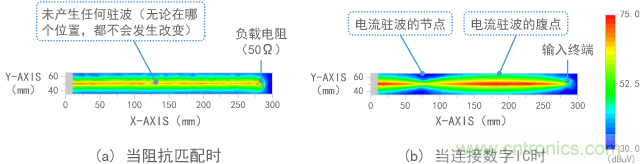
圖11 磁場(電流)的測量結果

圖12 電場(電壓)的測量結果
(5) VSWR
圖12所示電壓駐波的波腹(最高點)和波節(最低點)之比率稱為VSWR(電壓駐波比率),它是表示反射程度的指數。對于電壓和電流而 言,VSWR趨于一致。如果沒有駐波,VSWR為1。反射越強,VSWR的值越大。根據圖中的測量結果,(b)中觀察到了駐波,指示VSWR約為4。
(6) 駐波周期為二分之一波長
駐波一個周期(波節到波節)的長度為頻率的二分之一波長。因為后面將要講述的阻抗變化和傳輸線諧振是以此駐波為基礎的,它們可能在使傳輸線長度為二分之一波長整數倍的每個頻率處反復出現。
圖11和圖12(b)的示例表明駐波的一個周期約為200mm,這說明傳輸線上的一個波長為400mm。在真空條件下測量的490MHz 處的波長約為600mm,這表明在該傳輸線上波長縮短至三分之二。這個縮短比率會隨著基板的相對介電常數而變化,介電常數越大,波長就會越短(這意味著電 波在基板上減緩)。
[page]阻抗因傳輸線路而變化
(1) 什么讓阻抗出現變化?
從傳輸線的角度而言,信號線的另一個重要特性在于通過信號線的負載阻抗與阻抗本身完全不同。
例如,在連接至圖1所示20cm長信號線的數字IC的輸出終端,阻抗是多少?為找出答案,連接一個電阻器(10Ω: 紫色,1000Ω: 藍色)、一個電容器(5pF: 綠色)和一個電感器(50nH: 紅色)作為負載(如圖13所示),并測量阻抗。如果數字IC如圖1所示連接到終端端口,阻抗可能接近于電容器(5pF)的阻抗。
圖14指出了計算模型。(a)表示不考慮信號線的情形,而(b)顯示通過傳輸線路測量的情形。此外,(c)給出了按照第3章的章節3-2所述以線路模擬單級LC電路的情形,僅供您參考。
計算結果如圖15所示。情形(a)(未考慮信號線)指出不考慮電阻器情況下的恒定值。電感器和電容器分別顯示出與頻率成正比/反比的阻抗。
(2) 阻抗因傳輸線路而振蕩
相反,情形(b)(考慮傳輸線路)在10MHz頻率以上比(a)中的差異大,在100MHz頻率以上表現出復雜的波動情況。仔細觀察就會發現,阻抗似乎以信號線的特性阻抗(該示例中為123Ω)為中心,在其附近振蕩。如上所述,縱觀整條傳輸線路,阻抗在高頻范圍內似乎存在顯著差異。盡管圖15僅顯示了阻抗的振幅,但其相位也發生了變化。因此,根據不同頻率,電 感器可能類似于電容器,而電容器可能類似于電感器。(在某些情況下,利用這樣的特性,傳輸線路可以用作阻抗變換器或者用于阻抗匹配。)
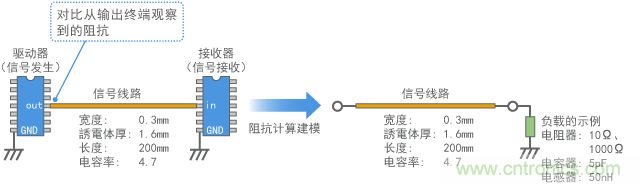
圖13 從數字電路輸出終端觀察到的阻抗
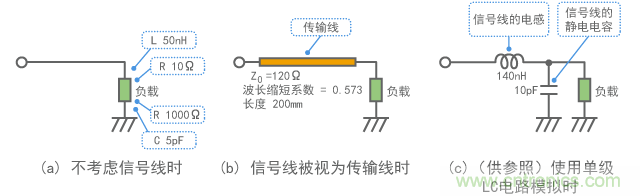
圖14 計算模型
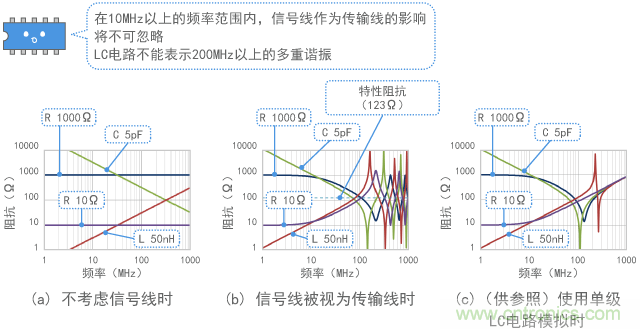
圖15 阻抗對比
(3) 入射波和反射波之間的相位差導致阻抗變化
在圖15(b)的計算結果中,連接5pF電容器的情形(綠線)表現出的特征相對接近使用數字電路作為負載的情形。計算結果表明100MHz 到200MHz之間存在局部最大阻抗。在200MHz以上頻率范圍內,阻抗交替出現局部最高點和局部最低點,呈現出周期變化。阻抗的局部最低點和下一個局 部最低點之間的頻率間隔等于使導線長度為二分之一波長的頻率。如上所述,傳輸線的態勢與導線長度和波長之間的關系有著密切的關聯。
(4) 注意導致局部最小阻抗的頻率處的噪聲
因為導致局部最小阻抗的頻率容許很大的電流,所以需要特別注意EMC措施。脈沖波形可能導致振鈴或者可能發射很強的噪聲。







