【導讀】本文描述與模數轉換器本身相關的誤差。本文還將揭示轉換器內部的不精確性累積到何種程度即會導致這些誤差。定義新設計的系統參數時,若測量精度極為重要,那么這些內容對于理解如何正確指定一個ADC有著重要作用。最后,本文將討論一個簡單的誤差分析,幫助為設計選擇正確的轉換器。
模數轉換器(亦稱為ADC)廣泛用于各種應用中,尤其是需要處理模擬傳感器信號的測量系統,比如測量壓力、流量、速度和溫度的數據采集系統(僅舉數例)。一般而言,這些信號屬于時域簽名,以脈沖或階躍函數的形式出現。
在任何設計中,理解這些類型應用的總系統精度始終都是非常重要的,尤其是那些需要對波形中極小的靈敏度和變化進行量化的系統。理想情況下,施加于信號鏈輸入端的每一個伏特都由ADC以數字表示一個伏特的輸出。但是,事實并非如此。所有轉換器和信號鏈都存在與此相關的有限數量誤差。
ADC的不精確性
無論何種信號鏈,轉換器都是系統的基本要素。為設計選擇的任何ADC都會決定系統的總精度。換言之,系統精度不可能高于轉換器的最低有效位(LSB)大小。為了表明這一點,讓我們來看一個簡短的ADC不精確性指南。
首先,注意到由于ADC不是理想的,并且分辨率有限,因此它們在輸出端只能顯示有限數量的信息表示。表示的信息數量由轉換器滿量程輸入除以2N表示,N為轉換器的理想位數。
例如,假設選擇一個12位ADC,則它可在輸出端以4096個數字表示施加于轉換器輸入端的任何信號。這些表示信息確實存在有限量的誤差。因此,如果12位ADC的輸入滿量程(VFS)為10 V p-p,那么其理想情況下的LSB大小為2.44 mV p-p,精度為±1.22 mV。
而實際上,ADC是非理想的。在轉換器內部存在一定噪聲,
甚至直流中也有噪聲。記住,1 kΩ電阻等效于4 nV? Hz (1 Hz帶寬,25°C)。注意,查看12位ADC數據手冊時,SNR通常為大約70 dB到72 dB。但是,根據下列公式,一個12位ADC理想情況下應當具有74 dB:
因此,實際上12位分辨率是無法達到的,因為轉換器本身存在一定的不精確性,如圖2所示。
這些不精確性或誤差決定了轉換器表示信號的效率,并最終為信號鏈所接收。失調誤差定義為傳遞函數無法通過零點的模擬值。增益誤差是失調誤差為零時理想與實際傳遞函數之間的滿量程數值之差。通常意義上的線性度誤差或非線性度是指零電平與滿量程之間的直線偏差,如圖1所示。
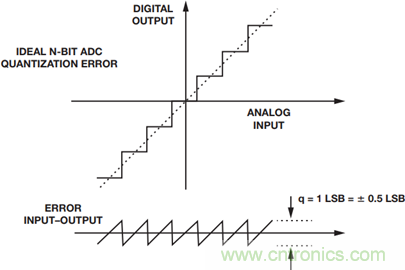
圖1. ADC量化誤差
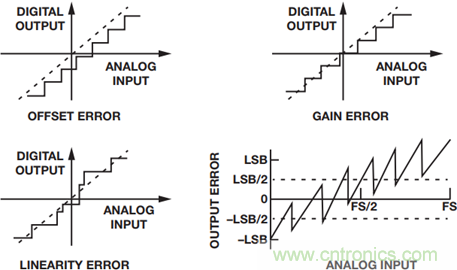
圖2. ADC的不精確性
有關ADC不精確性的更多信息
對最基本的模數轉換器誤差進行定義并有所了解后,再說明這些誤差的區別會有些幫助。大部分ADC的失調和增益都存在這種小誤差,通常可以忽略或通過外部模擬電路調節(消除),或者采用數字技術校正。然而,諸如線性度、量化和溫度系數等其他誤差無法輕易調節或消除。
模數轉換器線性度只與轉換器自身有關,即取決于架構和工藝變化。有很多方法可以校正,但都很昂貴。設計人員有兩種選擇:購買更好、成本更高的轉換器,或采用數字手段校正線性度。數字校正的成本也十分高昂。這意味著可能需要更多資源來指定DSP或FPGA,因為線性度會隨溫度和工藝的變化而改變。根據采樣速率、IF和分辨率,數字校正可能需要廣泛的特性表述和查找表,以便即時校正或調節ADC的性能。
線性度有兩種類型的誤差:它們是差分非線性和積分非線性,通常分別稱為DNL和INL。DNL定義為偏離理想值的一切誤差或偏差。換言之,它表示兩個相鄰代碼的模擬差與理想代碼值VFS/2N之間的偏差。可將其看作與ADC的SNR性能相關的因素。隨著代碼的偏差越來越大,轉換數也隨之下降。該誤差在溫度范圍內的界限為±0.5 LSB,可保證無失碼。
INL定義為零電平和滿量程之間的理想直線近似曲率偏差。多數情況下,INL決定了ADC的SFDR性能。INL總偏差形狀可以決定最主要的諧波性能。比如,INL曲線呈弓形會相應產生更差的偶次諧波,而INL曲線呈S弓形則通常產生奇次諧波。該誤差本質上與頻率有關,并與這類誤差分析無關。
哪怕可以消除靜態失調和增益誤差,與失調和增益誤差有關的溫度系數將會依然存在。
例如,一個12位ADC具有10 ppm增益誤差,或FSR/°C = 0.001%/°C.
12位系統中的1 LSB為¼096,或者近似等于0.024%。
因此,若125°C Δ (–40°C至+85°C),則產生±2.5 LSB增益溫度系數誤差,或0.001% × 125 = 0.125%。
其中,0.125/0.024 = 5.1 or ±2.55 LSBs.
For offset tempco a 5 ppm offset error or FSR/°C = 0.0005%/°C.
這將產生±1.3 LSB失調溫度系數誤差,或0.0005% × 125 = 0.0625. 其中,0.0625/0.024 = 2.6 or ±1.3 LSBs.
ADC誤差分析
影響轉換器性能的其它誤差來源有:CMRR、時鐘抖動、固有電路板噪聲、耦合等等。所有這些誤差最終都決定了ADC如何有效地表示信號;通常在頻率域內ADC能更高效地表示自身。
從時域角度來看,分析轉換器的總精度需要了解下面五個誤差:
- 相對精度DNL,定義為±0.5 LSB
- 相對精度溫度系數和DNL溫度系數,通常包含在數據手冊的相對精度規格中。
- 增益溫度系數誤差,為±2.5 LSB (數據來源于上文示例)
- 失調溫度系數誤差,為±1.3 LSB (數據來源于上文示例)
- 電源靈敏度,通常以第一奈奎斯特區內的低頻PSRR (電源抑制比)表示。對于12位ADC而言,它一般可表示為60 dB或±2 LSB。
只需進行方和根(RSS)運算,所有這些誤差源構成±3.5 LSB總轉換器誤差。這個結果可能過于悲觀了。然而,統計容差結果可能過于樂觀了,或者總誤差之和除以誤差數,即(0.5 + 2.5 + 1.3 + 2)/4 = ±1.58 LSBs。ADC實際容差應當介于這兩種思路或方法之間。
因此,當在轉換器中加入精度誤差的時候,或者進行任何系統精度分析的時候,設計人員應當使用加權誤差源法,然后對這些誤差源進行RSS計算。這是確定ADC總誤差的最佳方法。因此,±0.5 LSB的相對精度應當保持在100%。然而,±2.5 LSB增益溫度系數誤差應當是總誤差的66%,或2.5/(0.5 + 1.3 + 2) × 100。±1.3 LSB的失調溫度系數誤差將為總誤差的26%,或1.3/(0.5 + 2.5 + 2) × 100。±2 LSB的電源靈敏度誤差將為總誤差的47%,或2/(0.5 + 1.3 + 2.5) × 100。將這些加權誤差以RSS方式相加,或者進行平方根計算
ADC帶寬精度
ADC還有建立時間精度。記住,轉換器的內部前端需要具有足夠的帶寬(BW),才能精確地對信號進行采樣。否則,累積誤差將大于上文討論的結果。
一般而言,一個ADC的內部前端需要在半個周期或采樣時鐘周期內建立(0.5/Fs),這樣才能提供對內模擬信號捕捉的精確表達。因此,對于一個12位ADC(采樣速率為2.5 GSPS,滿量程輸入范圍為1.3 V p-p)來說,全功率帶寬(FPBW)可通過下列瞬態公式推導:
求解t:
代入 τ = 1/(2 × π × FPBW),一個時間常數,求解FPBW:
現在,令t = 0.5/Fs,則樣本建立所需的時間如下(樣本周期為1/Fs):
這樣會使ADC內部前端所需的帶寬或FPBW最小。這是轉換器內部前端建立至1 LSB以內并正確采樣模擬信號所需的帶寬。為了滿足這類ADC的1 LSB精度要求,這將會需要花費數個時間常數。
一個時間常數為24 ps或 τ = 1/(2 × π × FPBW)。要了解ADC滿量程范圍內達到LSB尺寸要求所需的時間常數數量,就需要找出滿量程誤差或%FS。或者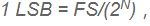 其中N = 位數,或
其中N = 位數,或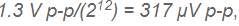 且%FS = (LSB/FS) × 100 = 0.0244.
且%FS = (LSB/FS) × 100 = 0.0244.
通過描繪歐拉數或eτ,可以繪出一條曲線,以便每次通過常數都能方便地看出相對誤差。如圖3可見,12位ADC樣本建立至大約1 LSB以內需時8.4個時間常數。
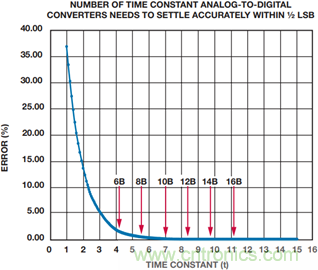
圖3: 建立精度與時間常數的關系
這樣,設計人員便能估算用于轉換器的最大模擬輸入頻率或采樣帶寬,并依舊建立至1 LSB誤差以內。超出這個范圍,則ADC無法精確表示信號。 這可以簡單定義為:FMAX = 1/(τ × 時間常數數量) 或 1/(24 ps × 8.4) = 4.96 GHz.
記住,這里表示的是最佳情形,并假定采用單極點ADC前端。并非所有現實中的轉換器都以這種方式工作,但這是一個很好的開端。例如,上文描述的模型最高可適用至12位,但針對14/16位以及更高位則需要根據這些細微影響采用二階模型,以使建立時間擴展至預測的一階模型以外。
關于ADC帶寬的簡要說明
記住,ADC全功率帶寬不同于上文定義的轉換器可用帶寬或采樣帶寬。它可以當成是模擬信號輸入運算放大器的全功率帶寬(FPBW),信號更像是三角波信號,并且輸出端存在大量失真。FPBW是ADC精確捕捉信號并使內部前端正確建立所需的帶寬(前文示例中為6.62 GHz)。選擇一個IF并在該范圍內使用轉換器不是一個好主意,因為系統的性能結果會大幅改變;在大約5 GHz處,如上文示例所示,根據轉換器數據手冊中的額定分辨率和性能指標,滿量程帶寬遠高于轉換器自身的最大采樣帶寬。設計是圍繞采樣帶寬而展開的。所有設計都應當避免使用額定全功率帶寬的某一或全部最高頻率部分,否則動態性能(SNR/SFDR)會下降并大幅改變。為了確定高速ADC的采樣帶寬,應當使用上文中的示例,因為這些數據并非總能從數據手冊中獲取。通常,數據手冊會規定甚至列出轉換器采樣帶寬內經過生產測試、能夠保證額定性能的頻率。然而,在較老的ADC產品中這些測試頻率在數據手冊中并不總是以FMAX來定義。今后還需要對行業中的這些帶寬術語做出更好的說明、定義和測試。
結論
本文給出了有關如何查看一般靜態ADC的不精確性誤差和涉及帶寬的ADC不精確性誤差的指導說明。還提供了針對ADC誤差以及這些誤差如何影響信號鏈的更深入解釋。請記住,并非所有的元件都采用相同的方式構建,這對于有源和無源器件來說都是正確的。創建囊括所有這些誤差的電子表是插入不同信號鏈元件的簡便方法,可更快進行評估并決定元件的權衡取舍。這在元件之間進行成本、尺寸和功耗的權衡取舍以及衡量信號鏈性能差異方面尤為如此。
進行下一款信號鏈設計時,應牢記這些原則。提出申請后,我們將為您發送一份電子表格分析,其中會強調上文提到的示例。您可隨意使用該電子表格,以滿足您的設計需要。若您有任何其它問題,請通過ADI EngineerZone®,(在線技術支持社區)與我聯系,或者通過 RReeder與我聯系。
有關如何生成完整的信號鏈分析將在《第二部分:模擬信號鏈精度》中進行討論。最后,請記住,單純增加信號鏈中ADC的性能或分辨率無法提升測量精度。如果依舊存在同樣數量的前端噪聲,精度將不會得到改善。只會讓噪聲測量達到更精細的程度,并最終可能讓設計人員的老板付出更多的成本。
參考電路
AN010應用筆記,信號分析儀的動態范圍測量. LDS Dactron, 2003。
Bennett, William R."量化信號頻譜",Bell System技術雜志,第27卷,1948。
Bennett, William R."PCM系統內噪聲",Bell Labs Record,第26卷,1948。
Brad Brannon,AN-410應用筆記"通過擾動消除轉換器非線性",ADI公司,1995。
Gyorki, John R. 信號調理與PC數據采集手冊,第三版,1-11。
Kester, Walt. "模數轉換:研討會系列" ,模數轉換,ADI公司,2004。
整體精度 = ENOB (有效位數),數據轉換。
Ruscak, Steve和Larry Singer。利用直方圖技術測量模數轉換器噪聲,模擬對話,第29-2卷,1995。
"系統衰減預算、精度、分辨率" Dataforth.
Titus, John. "分辨率和精度: 相似,并不相同" 。Design News, 2003.
本文轉載自亞德諾半導體。
推薦閱讀:








