【導讀】上一篇文章討論了濾波器相位與濾波器實現拓撲之間的關系,本篇將討論濾波器傳遞函數本身的相位漂移。雖然濾波器主要是針對幅度響應而設計的,但在延時仿真、級聯濾波器電路特別是過程控制環路等應用中相位響應非常重要。
本文主要討論低通和高通響應。后續系列文章還將討論帶通和陷波(帶阻)響應、全通響應以及濾波器的脈沖與階躍響應。
回顧以前的文章可知,有源濾波器的傳遞函數可以被看作是濾波器傳遞函數和放大器傳遞函數的級聯響應(圖1)。
圖1. 以兩個級聯的傳遞函數的形式表示的濾波器。
低通傳遞公式
首先,我們再看一下傳遞公式的相位響應。
對于單極點低通濾波器,傳遞函數的相移等于:
其中ω代表角頻率(ω = 2π f 弧度每秒,1 Hz = 2π 弧 度 每 秒),ω0代表濾波器的弧度 中心頻率。中心頻率也可被看作是截止頻率。就相位 而言,中心頻率是相移在整個范圍一半處的頻率。由于角頻率用在比值公式中,因此f/f0完全可以代替ω/ω0。
圖2(左軸)是在中心頻率以下二十倍頻到中心頻率以上二十倍頻范圍內對公式1的 求值 結果。由于單 極 點低 通濾 波器 具 有90°的相移范圍—從0°至90° —中心頻率的相移為-45°。當ω = ω0時,歸一化中心頻率等于1。
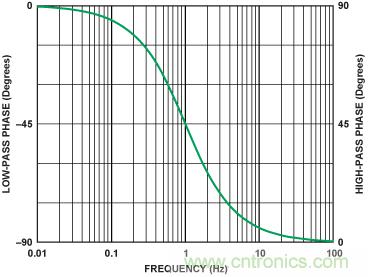
圖2. 中心頻率為1的單極點低通濾波器(左軸)和高通濾波器(右軸)的相位響應
同樣,單極點高通濾波器的相位響應等于
圖2(右軸)是在中心頻率以下二十倍頻至中心頻率以上二十倍頻范 圍內對公式2的求值結果。中心頻率 (=1) 的相移等于+45°。
如果低通通帶定義為截止頻率以下的頻率,高通通帶定義為中心頻率以上的頻率,那么最小相移(0°至45°)應在通帶內。反之,最大相 移(45°至90°)發生在阻帶內(頻率高于低通截止頻率并且低于高通截止頻率)。
在低通情況下,濾波器輸出滯后于輸入(負相移);在高通情況下,輸出領先于輸入(正相移)。圖3顯示了相關波形:輸入正弦波信號(中間曲線),截止頻率為1k H z 的單極點高通濾波器輸出信號(頂部曲線),截止頻率為1k H z的單極點低通濾波器輸出信號(底部曲線)。信號頻率也是1k H z—兩個濾波器的截止頻率。圖中波形領先和滯后45°顯而易見。
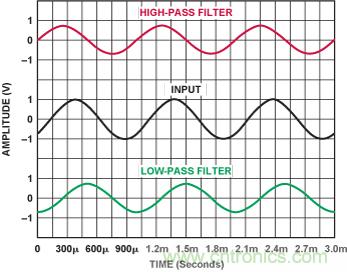
圖3. 輸入(中間曲線)、單極點高通濾波器輸出(頂部曲線)和低通濾波器輸出(底部曲線)。
二階低通濾波器傳遞函數的相移可以近似表示為:
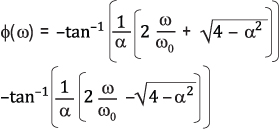 (3)
(3)圖4(左軸)是在中心頻率以下二十倍頻至中心頻率以上二十倍頻范 圍內對公式3的求值結果(代入α= √2 = 1.414)。這里的中心頻率等于1,相移為-90°。
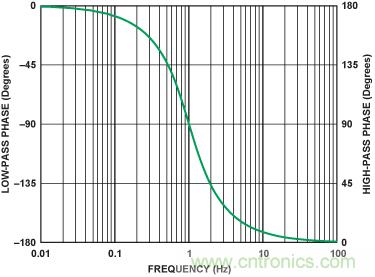
圖4. 中心頻率為1 的雙極點低通濾波器(左軸)和高通濾波器(右軸)的相位響應
在公式3中,α是濾波器的阻尼比,等于Q的倒數(即Q = 1/α)。它決定了幅度(和瞬態)響應中的峰值和相位變化的尖銳度。α等于1.414很 好地表征了雙極點巴特沃斯(最大平坦度)響應。
雙極點高通濾波器的相位響應可以被近似表示為:
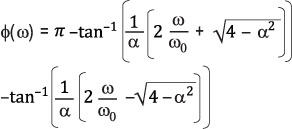 (4)
(4)圖4(右軸)是在中心頻率以下二十倍頻至中心頻率以上二十倍頻范 圍內對公式4的求值結果(α=1.414)。在中心頻率(=1) 點,相移為90°。
圖2和圖4只使用了一條曲線,這是因為高通和低通相位響應是相似的,只是相移分別是90°和180° (π/2和π弧度)。這等效于相位符號的改變,導致低通濾波器輸出滯后而高通濾波器領先。
在實際使用中,高通濾波器其實是一個寬帶帶通濾波器,因為放大器的響應至少會引入一個低通單極點。
圖5是雙極點低通濾波器的相位響應和增益響應,圖中給出了不同Q值時的曲線。這個傳遞函數表明,相位變化遍布在相當寬范圍的頻 率上,而變化的范圍與電路Q值呈反比關系。雖然本文主要討論相位響應,但相位變化率和幅度變化率之間的關系也值得我們認真思考。
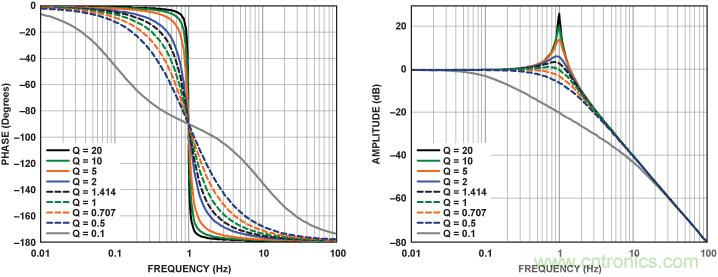
圖5. 作為Q函數的雙極點低通濾波器電路的相位和幅度響應。
值得注意的是,每級雙極點電路提供最大180°的相移,在極端情況下,相移–180°,雖然滯后360°,但這個角度與180°相移具有相同的屬 性。基于這個原因,多級濾波器的傳遞函數圖形經常在一個限定范圍內,比如180°至–180°,以提高圖形讀取的準確性(見圖9和圖11)。 在這種情況下,我們必須認識到,圖形上的角度實際上是真正的角度加上或減去m×360°。雖然在這種情況下圖形的頂部和底部會出 現不連續(因為圖形變化了±180°),但實際相位角度的變化是平滑和單調的.
圖6給出了不同Q值下雙極點高通濾波器的增益和相位響應。這個傳遞函數表明,180°的相位變化可以發生在很大的頻率范圍內,而變 化的范圍反比于電路Q值。另外值得注意的是,曲線的形狀非常類似。 特別是相位響應具有相同的形狀,只是覆蓋范圍不同。
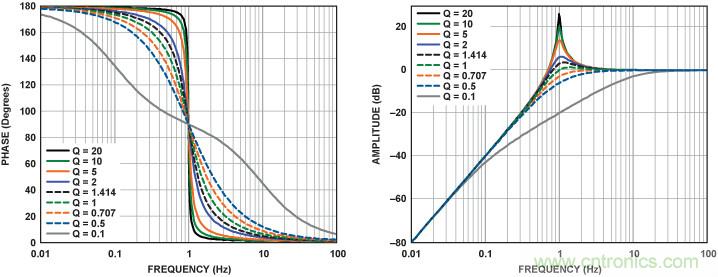
圖6. 作為Q 函數的雙極點高通濾波器的相位與幅度響應。
放大器傳遞函數
放大器的開環傳遞函數基本上就是單極點濾波器的傳遞函數。如果是反相放大器,效果上等同于插入180°的額外相移。放大器的閉 環相移通常被忽略,但如果它的帶寬不夠的話,將影響復合濾波器的總傳遞函數。本文選用了A D822進行濾波器仿真。 A D822將影響復合濾波器的傳遞函數,但只是在較高頻率處,因為它的增益和相移保持在比濾波器本身的轉折頻率高得多的頻率。從數據手冊上摘錄 的AD822開環傳遞函數見圖7。
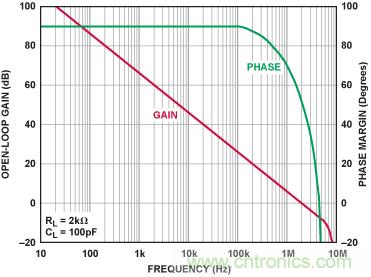
圖7. A D822 增益和相位波特圖。
例1:1kHz、5極點、0.5dB切比雪夫低通濾波器
下面舉一個1k Hz、5極點、0.5dB的切比雪夫低通濾波器例子進行討論。選擇這個特定例子的原因如下:
1) 與巴特沃斯濾波器不同,切比雪夫濾波器各級電路的中心頻率是完全不同的,這樣能使圖形上的曲線伸展得更開一些,使得圖形更加有趣。
2) 電路的Q值一般要高一點。
3) 奇數個極點可以突出單極點和雙極點電路之間的區別。
濾波器部分采用ADI網站上提供的濾波器設計向導進行設計。
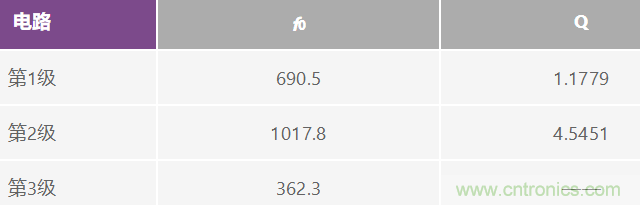
這部分電路的f0和Q見下表:

圖8是整個濾波器的原理圖。所選擇的濾波器拓撲— 多反饋 (M F B)—又是任意的,這種選擇使得單極點部分是一個有源積分器,而不是簡單緩沖的無源RC電路。
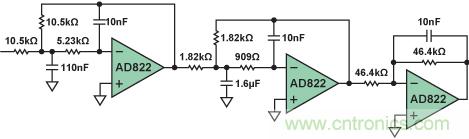
圖8. 1kHz、5 極點、0.5dB切比雪夫低通濾波器。
圖9給出了整個濾波器的各級電路的相移。圖上顯示了單獨第一級電路(第1級 — 藍 色)、前面兩級電路(第1和第2級 — 紅色)和整個 濾波器(第1、第2和第3級—綠色)的相移。這些相移包含了濾波器部分的基本相移、每個反相放大器貢獻的180°相移和放大器頻率響應對總相移的影響。
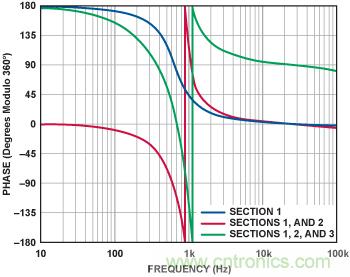
圖9. 圖8 所示1kHz、5極點、0.5dB切比雪夫低通濾波器的相位響應。
讓人感興趣的一些細節:首先,作為凈滯后的相位響應是負相加的。 由于在低頻段放大器的倒相,第一個雙極點電路開始相位是–180°(=180°以360°為模),在高頻段增加到–360°(=0°以360°為模)。第 二級電路增加另外一次倒相,開始相位是–540°(=180°以360°為模),在高頻段相位增加到–720°(=0°以360°為模)。第三級電路在低頻 段的相位開始于–990°(=180°以360°為模),在高頻段增加到–990°(=90°以360°為模)。另外需要注意,當頻率超過10k H z 時,由于放大器的頻率響應,相位將發生輕度的滾降。這種滾降是累積的,每級電路都會有所增加。
例2:1kHz、5極點、0.5dB切比雪夫高通濾波器
第二個例子(見圖10)考慮的是一個1kHz、5極點、0.5dB切比雪夫高通濾波器的相位響應。在這個例子中,濾波器采用S allen-Key 壓控電壓源(VC V S) 電路而不是多反饋 (M F B) 進行設計(仍使用濾波器設計向 導)。雖然是任意選擇的,但VCVS 只需要每級雙極點電路兩個電容,不像MFB中的每級電路三個電容,而且前兩級電路是同相的。
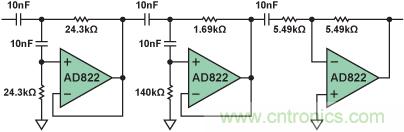
圖 10:1kHz、5極點、0.5dB切比雪夫高通濾波器。
圖11給出了濾波器中每級電路的相位響應。第一級電路相移開始于低頻段的180°,高頻段下降到0°。第二級電路在低頻段增加了180°,開始于 360°(=0°以360°為模),在高頻段下降到0°。第三級電路增加了一次倒相,開始于低頻段的–180°+90°=-90°,在高頻段下降到–540°(= –180°以360°為模)。請再次注意,由于放大器的頻率響應,在高頻 段會有額外的滾降發生。
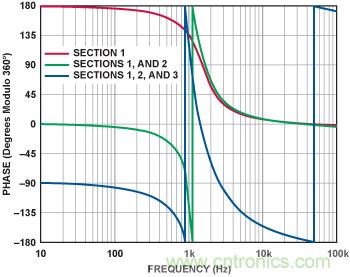
圖11:圖10 所示1kHz、5極點、0.5dB切比雪夫高通濾波器的相位響應。
結束語
本文討論了低通和高通濾波器的相移特性。這個系列中的前一篇文章介紹了相移與濾波器拓撲之間的關系,在后續文章中,我們還將 討論帶通、陷波和全通濾波器—最后,我們會對所有內容進行回顧,并介紹相移將如何影響濾波器的瞬態響應,同時討論群延時、脈沖響應和階躍響應。
附錄
單極點和雙極點的低通和高通濾波器的通用傳遞函數見公式A1到公式A4。
單極點低通濾波器的傳遞函數:
其中 s = jω and ω0 = 2πf0.
雙極點有源低通濾波器的傳遞函數:
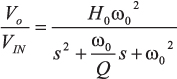 (A2)
(A2)其中 HO 是這級電路增益。
單極點高通濾波器的傳遞函數:
雙極點有源高通濾波器的傳遞函數:
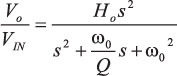 (A4)
(A4)1k Hz、0.5dB 切比雪夫低通濾波器的f0和Q值如下:
推薦閱讀:








