【導讀】在本系列的第一篇文章中,我考察了濾波器相位與濾波器實 現拓撲結構的關系。在第二篇文章中,我考察了低通和高通 響應濾波器傳遞函數的相位偏移。這篇文章將重點討論帶通 響應。雖然濾波器主要針對幅度響應而設計,但在一些應用 中,相位響應可能非常重要。
出于考察目的,有源濾波器的傳遞函數實際上是濾波器傳遞 函數和放大器傳遞函數的級聯(見圖1)。

圖1. 濾波器作為兩個傳遞函數的級聯。
帶通傳遞函數
把低通原型的分子改為
結果將把濾波器變成一個帶通 函數。這會在傳遞函數內引入一個零點。分子中的一個s得到 一個零點,分母中的一個s得到極點。零點將產生頻率上升響 應,而極點將產生頻率下降響應。
二階帶通濾波器的傳遞函數變為:
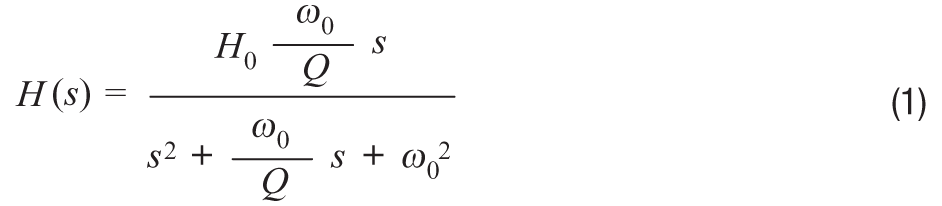
此處的ω為濾波器增益峰值化時的頻率 (F0 = 2 π ω0)
H0 為電路增益(Q峰值化),定義為:
其中,H為濾波器實現的增益。
對帶通響應來說,Q有特殊意義。它是濾波器的選擇性。定義為:
其中,FL和FH為響應比最大值相差–3 dB時的頻率。
濾波器的帶寬 (BW) 定義為:
可以證明,諧振頻率 (F0)為 FL 和 FH的幾何平均值,這就意味著,F0 在對數尺度上將出現在FL 和 FH 二者的中點。
另需注意的是,在對數尺度上,帶通響應的波裙在 F0 左右始終是對稱的。
帶通濾波器對各種Q值的幅度響應如圖2所示。在此圖中,中心頻率的增益歸一化為1 (0 dB)。
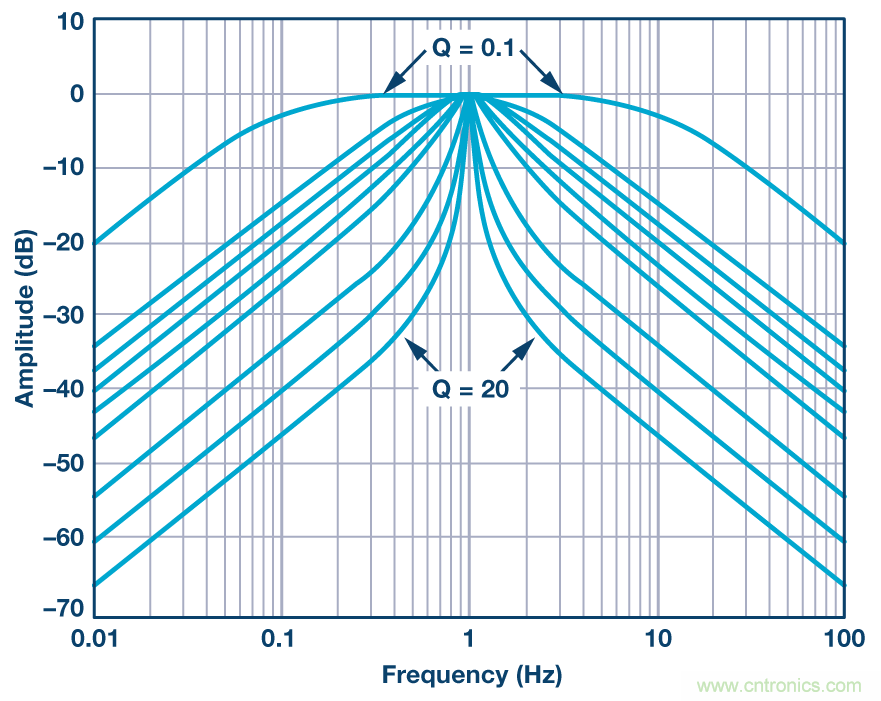
圖2. 歸一化的帶通濾波器幅度響應
雖然本文主要關注相位響應,但了解下濾波器幅度響應也很有用。
這里需要提醒一下。帶通濾波器有兩種定義方式。窄帶情況為經典定義,如上文所示。然而,在某些情況下,如果高、低截止頻率相差很大,則帶通濾波器采用獨立的高通和低通部分進行構造。這里所說的相差很大是說至少相差2個倍頻程(頻率×4)。這就是寬帶情況。本文中,我們主要關注窄帶情況。對 于寬帶情況,可將濾波器視為獨立的高通和低通部分。
雖然帶通濾波器可用巴特沃茲、貝塞爾或切比雪夫等標準響應定義,但它們也通常按照其Q和F0定義。
帶通濾波器的相位響應為:
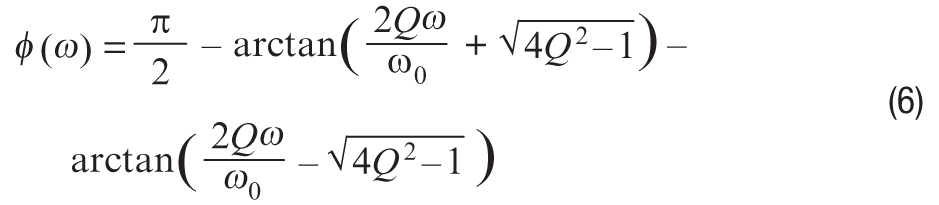
請注意,不存在單極點帶通濾波器。
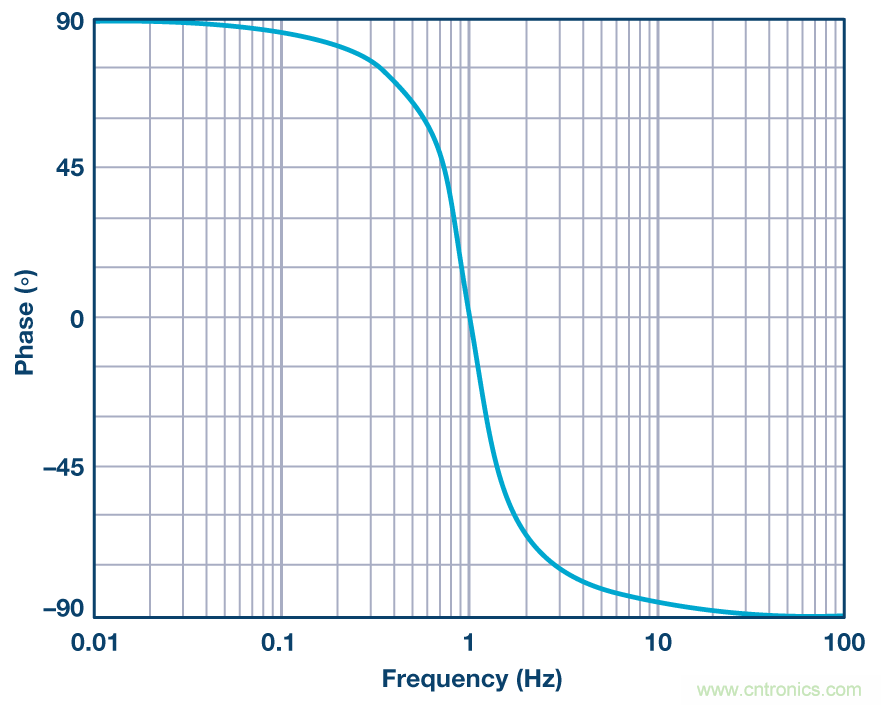
圖3. 歸一化的帶通濾波器相位響應
圖3從中心頻率的1%到中心頻率的100倍對公式6進行估值。中心頻率的相移為0°。中心頻率為1,Q等于0.707。此Q與前一篇文章中使用的Q相同,但該篇文章中我們使用的是α。記 住,α = 1/Q。
觀察后發現,此曲線的形狀基本上與低通(和相應的高通) 的曲線形狀相同。但是,本例中相移從中心頻率下方90°開 始,在中心頻率處趨于0°,最后結束于中心頻率上方–90°。
在圖4中,我們考察了在Q不斷變化時帶通濾波器的相位響 應。觀察傳遞函數可以發現,相位變化可能發生在相對較大 的頻率范圍內,變化的范圍與電路的Q成反比。同樣,在觀察 后發現,曲線的形狀與低通(和高通)響應相同,僅范圍有 差異。
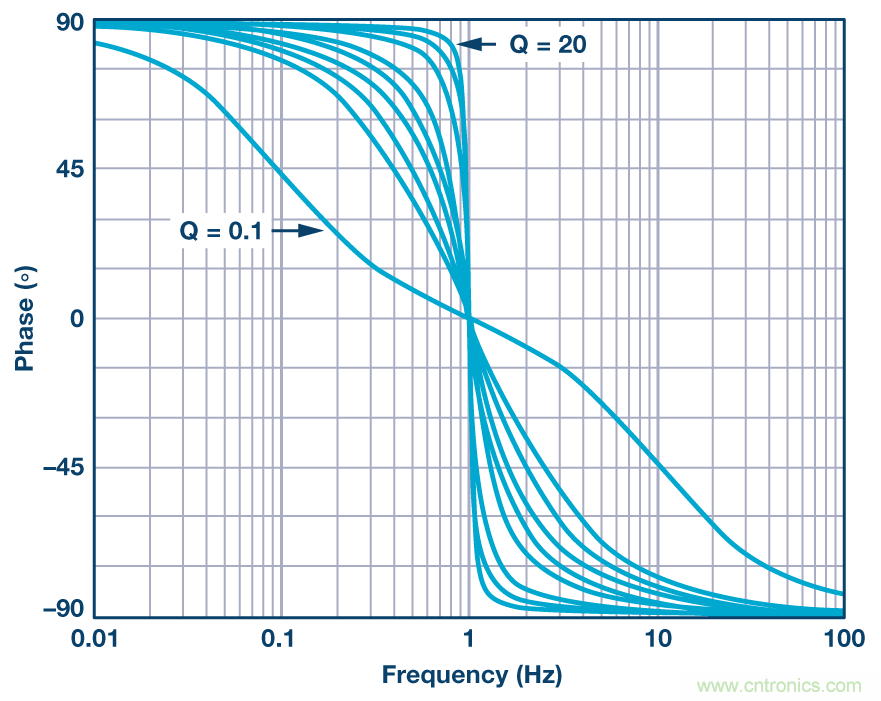
圖4. Q不斷變化時歸一化的帶通濾波器相位響應
放大器傳遞函數
之前的部分顯示,傳遞函數基本上就是單極點濾波器的傳遞 函數。雖然放大器的相移通常被忽視,但它可影響復合濾波 器的整體傳遞。本文隨機選擇了AD822 用于濾波器的仿真。 這樣選擇的部分原因是為了最大程度地降低對濾波器傳遞函 數的影響。這是因為,放大器相移的頻率明顯高于濾波器本 身的轉折頻率。AD822的傳遞函數如圖5所示,其信息直接取 自數據手冊。
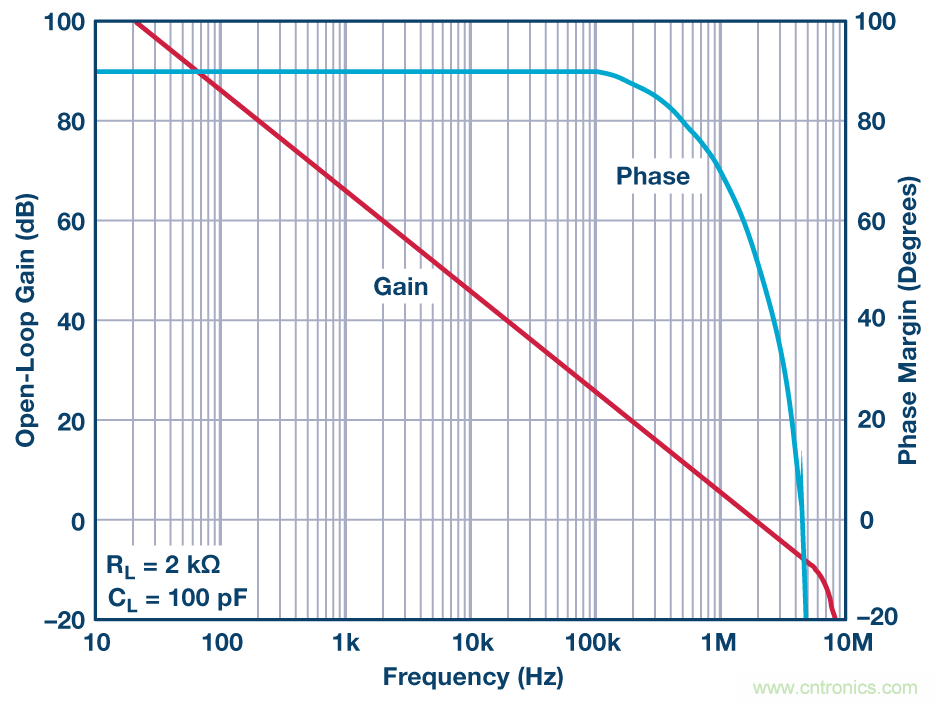
圖5. AD822波特圖增益和相位。
示例1:Q = 20 的1 kHz 2 極點帶通濾波器
第一個示例開始時是作為帶通設計的濾波器。我們隨意選擇 了一個1 kHz的中心頻率和數值為20的Q。由于Q在較高的一 側,因此我們將使用雙放大器帶通 (DABP) 配置。同樣,這 是隨意選擇的。
我們使用參考1的設計公式。相應的電路如圖6所示:
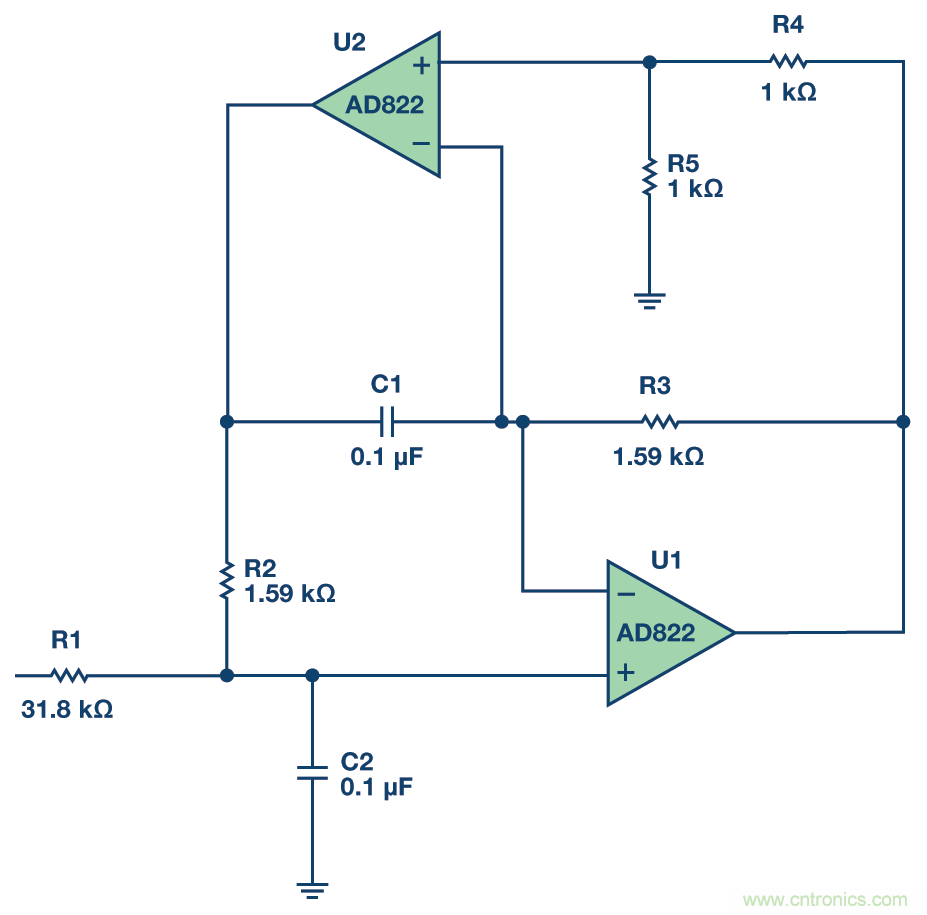
圖6. 1 kHz、Q = 20的DABP帶通濾波器。
本文中我們主要關注相位,但我認為考察下幅度響應也很有用。
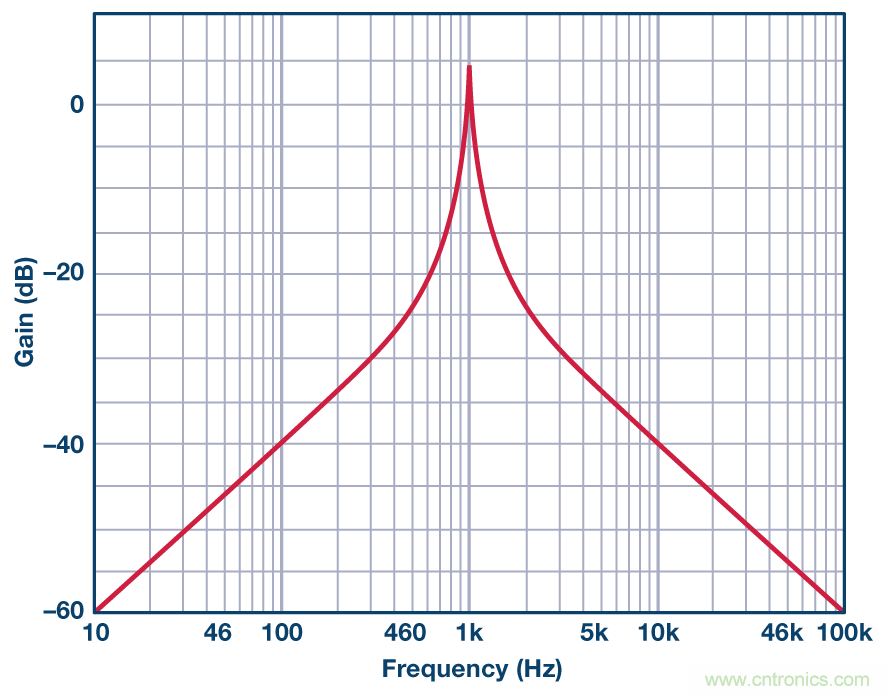
圖7. 1 kHz、Q = 20的DABP帶通濾波器幅度響應。
圖8所示為相位響應:
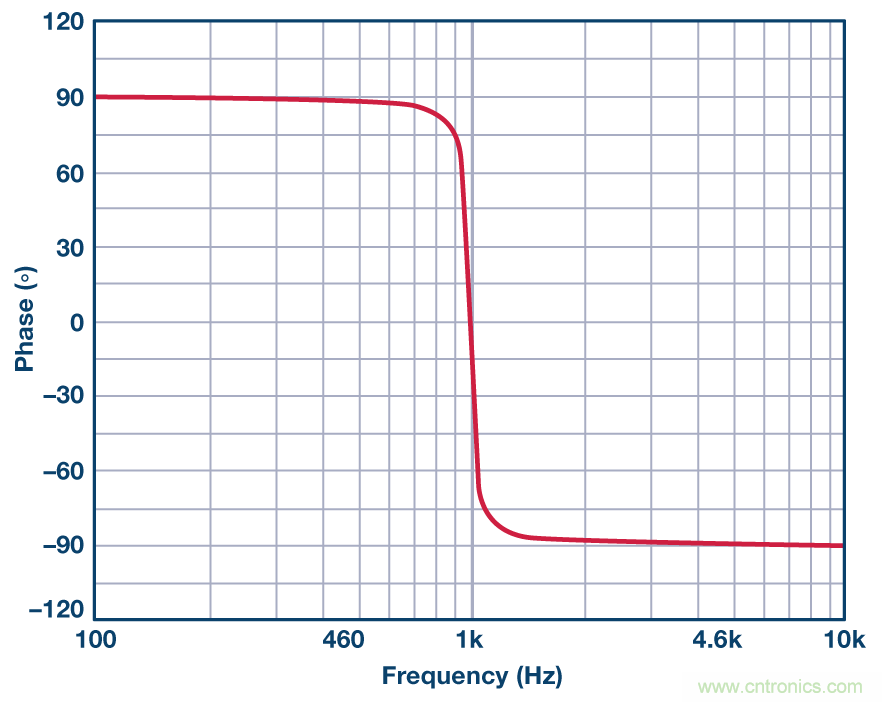
圖8. 1 kHz、Q = 20的DABP帶通濾波器相位響應。
應當注意,DABP配置為同相。圖8與圖3一致。
示例2:從1 kHz、3 極點0.5 dB 切比雪夫低通到帶通濾波器的轉換
濾波器原理以低通原型為基礎,低通原型可以其他形式表示。本例使用的原型是1 kHz、3極點、0.5 dB切比雪夫濾波器。選擇切比雪夫濾波器是因為,如果響應不正確,它可以 顯示得更清楚。例如,通帶中的紋波將不會排成一行。在本例中,巴特沃茲濾波器可能過于寬松。選擇3極點濾波器是為 了能夠轉換一個極點對和單個極點。
LP 原型的極點位置(來自參考1)為:
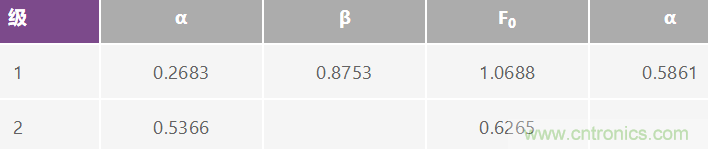
第一級為極點對,第二級為單極點。請注意,用α表示兩個完 全不同的參數的做法是不可取的。左側的α和β為復平面上的 極點位置。這些是轉換算法中使用的值。右側的α為1/Q,這 正是物理濾波器設計等式所希望看到的。
現在,低通原型被轉換成了帶通濾波器。參考1中列出的一系 列等式用于轉換。原型濾波器的每個極點都將轉換成一個極 點對。因此,轉換完成時,3極點原型將擁有6個極點(3個極 點對)。此外,原點處將有6個零點。不存在單極點帶通。
轉換過程的部分工作是指定可合成的濾波器的3 dB 帶寬。在 這種情況下,該帶寬將被設為500 Hz。產生的轉換結果如下:
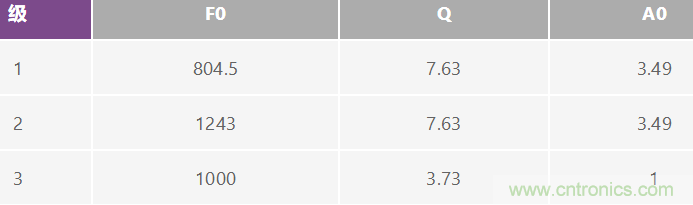
實際上,先將更低的增益和Q部分放入串中可能很有用,因為 這可最大程度地提高信號電平處理能力。前兩級存在增益要 求的原因在于,相對于總濾波器中心頻率,它們的中心頻率 將會衰減(也就是說,它們將在其他部分的波裙上)。
由于結果得到的Q適中(小于20),因而將選用多級反饋拓撲 結構。我們使用參考1中多路反饋帶通濾波器的設計方程設計 濾波器。圖9顯示了濾波器本身的原理圖。
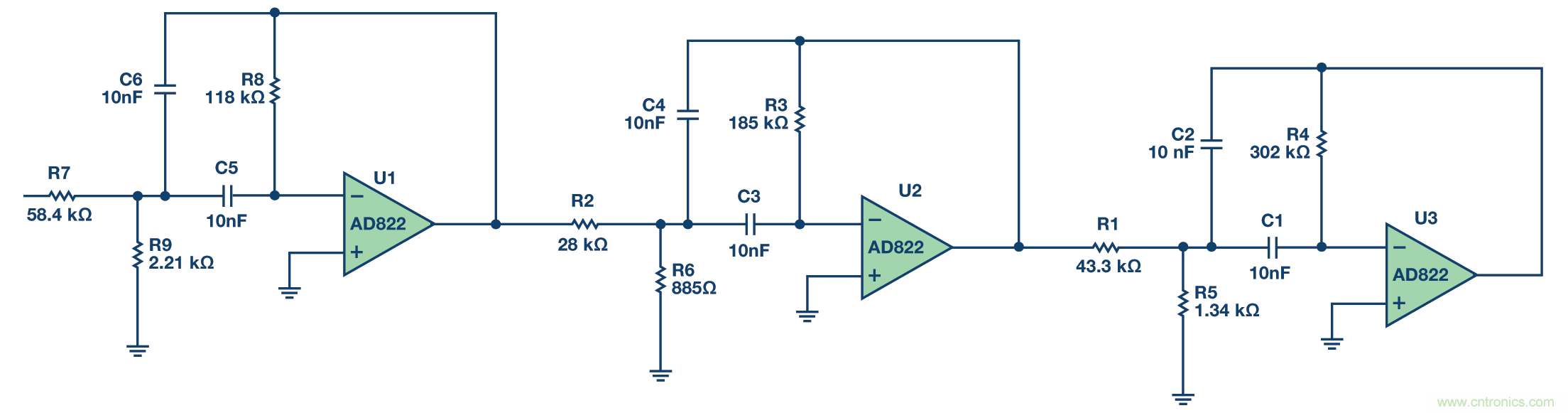
圖9. 1 kHz、6極點、0.5 dB切比雪夫帶通濾波器。
圖10中可以看到完整濾波器的相移。曲線圖單獨顯示了第一 部分的相移(第1部分)、前兩個部分的組合相移(第2部 分),以及完整濾波器的相移(第3部分)。這些曲線顯示了 "實際"濾波器部分的相移,其中包括放大器的相移和濾波器 拓撲結構的反相。
圖10中有幾點細節需要注意。第一,相位響應具有累積性。第 一部分顯示了180°的相位變化(濾波函數的相移,忽視了濾波 器拓撲結構的相移)。第二部分顯示了因具有兩部分而產生的 360°相位變化,每個部分180°。記住,360° = 0°。第三部分顯 示了540°的相移,每個部分180°。還應注意,在高于10 kHz的 頻率處,我們開始看到相位因放大器響應而輕微滾降。還可以 看出,滾降也具有累積性,會隨著每個部分而增大。
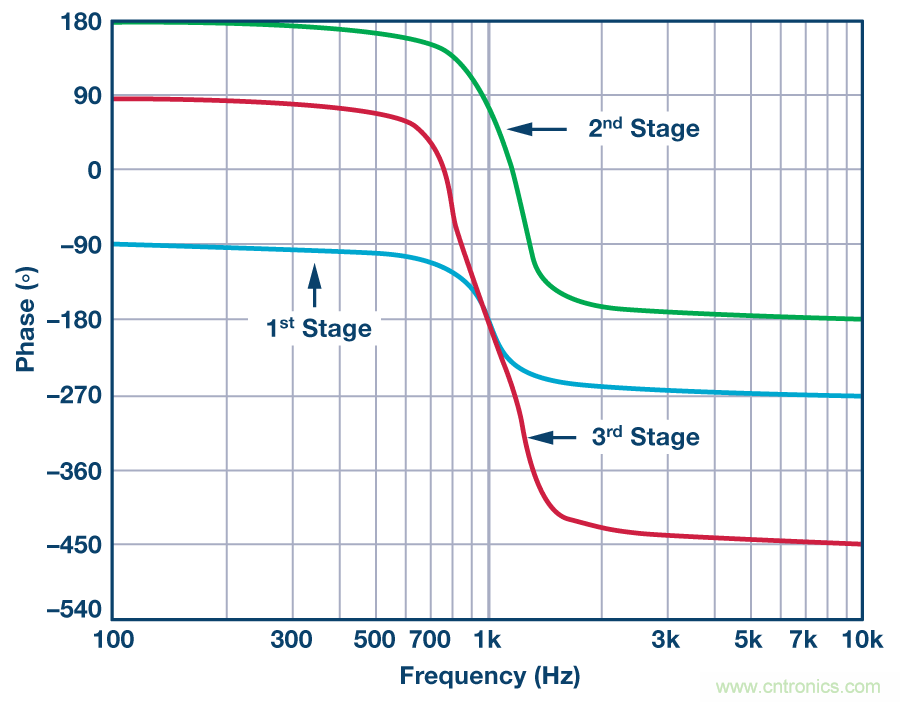
圖10. 1 kHz、6極點、0.5 dB切比雪夫帶通濾波器的相位響應。
在圖11中我們可以看到完整濾波器的幅度響應。
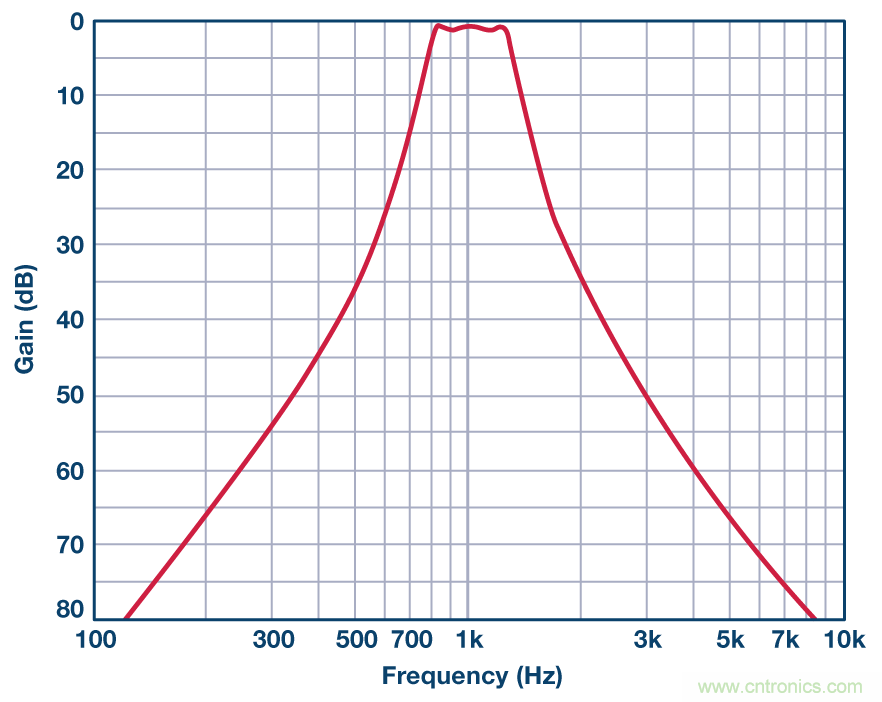
圖11. 1 kHz、6極點、0.5 dB切比雪夫帶通濾波器的幅度響應。
結論
本文討論的是帶通濾波器的相移。在前面幾篇文章中,我們 考察了與濾波器拓撲結構相關的相移以及低通和高通拓撲結 構的相移。在后續文章中,我們將考察陷波濾波器和全通濾 波器。在最后一期,我們將總結并考察相移如何影響濾波器 的瞬態響應,同時還會考察群延遲、脈沖響應、階躍響應, 以及它們對信號的意義。
推薦閱讀:








