【導讀】電流反饋放大器(CFA)歷來都不是跨阻放大器(TIA)的首選,因為它們具有較高的反相輸入電流和反相輸入電流噪聲,可能比同等級電壓反饋放大器(VFA)至少高出一個數量級。
簡介
電流反饋放大器(CFA)歷來都不是跨阻放大器(TIA)的首選,因為它們具有較高的反相輸入電流和反相輸入電流噪聲,可能比同等級電壓反饋放大器(VFA)至少高出一個數量級。另外,許多系統設計師對CFA并不熟悉,因為不大愿意使用它們。然而,事實上,CFA使用起來非常簡單,而且在要求高增益、低功耗、低噪聲、寬帶寬和高壓擺率的應用中,其性能可能超過VFA。其主要優勢之一是,一個理想CFA的環路增益獨立于其閉環增益,為此,CFA可以實現出色的諧波失真和帶寬性能,而不受其閉環增益的影響。
因超低的輸入偏置電流和輸入電流噪聲,FET輸入運算放大器往往是TIA應用的首選,尤其是將低輸出電流器件(如光電元件)用作輸入電流源的應用。盡管FET輸入放大器在諸多此類應用中技高一籌,但其速度卻可能無法滿足需要更快性能的系統要求。因此,在可以耐受較大噪聲、速度更快的系統中,越來越多地將CFA用作TIA。
本文旨在探討光電二極管或其他光-電流傳感器的寄生電容對用作TIA的CFA的影響,以及如何針對這種電容對放大器進行補償。同時簡要介紹CFA運行模式,并說明CFA和VFA分析法之間的相似之處。本文不使用VFA電路"噪聲增益"或者CFA電路"反饋阻抗"分析法。相反,采用基于環路增益的經典反饋理論,以避免在電流和電壓域之間來回轉換時遇到的困難(環路增益始終是一個無維度的量),而且該理論還可產生直觀、易用的波特圖。
電流反饋放大器的基本知識
理想的CFA的輸入阻抗為零——其輸入端跨接完全短路——因為負反饋信號為電流。相對地,理想的VFA的輸入阻抗則是無窮大,因為其反饋信號為電壓。CFA檢測在其輸入端中流過的誤差電流,并形成等于Z與輸入電流之積的輸出電壓,其中,Z表示跨阻增益。須正確定義誤差電流的方向,以產生負反饋。與VFA中的A相似,在理想CFA中,Z接近無窮大。圖1所示基本原理展示了如何將理想的CFA配置成TIA,以便將來自理想電流源的電流轉換為輸出電壓。
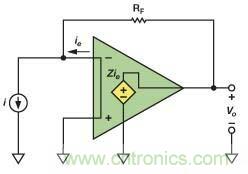
圖1. 用作TIA的理想CFA
該TIA的閉環增益可以表示為
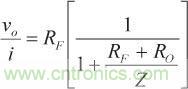 (1)
(1)等式1表示,Z接近無窮大,TIA增益則接近其理想值RF。隨著Z接近無窮大,誤差電流 ie接近零,所有輸入電流均流過RF。在等式1中,環路增益表示為
不幸的是,理想的CFA是不存在的,因此,實用器件一般都退而求其次:在其輸入端跨接一個單位增益緩沖器。電流鏡將誤差電流反射至一個高阻抗節點,在此,誤差電流被轉換成電壓,緩沖后饋入輸出端,如圖2所示。
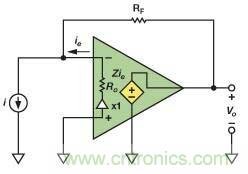
圖2. 用作TIA的實用CFA(帶單位增益緩沖器)
只要 Ro = 0,則閉環增益與等式1中的閉環增益相同。當Ro > 0時,閉環增益變成
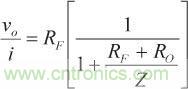 (2)
(2)且環路增益為
使用實用元件設計TIA
光電二極管和其他光電器件表現出一種與器件面積成比例的寄生分流電容。當 Ro = 0時,該電容完全自舉,因而不會影響閉環響應。在實際CFA中,Ro > 0,并且寄生電容會影響響應,結果可能導致電路不穩定。另外,就像VFA中的開環增益A一樣,在實際CFA中,Z的幅度在低頻下較大,隨著頻率的增加而滾降,而隨著頻率的增加,相移表現出更大遲滯。對于一階,Z(s)的特性可以描述為單個主極點,其中,s = p直流跨阻為Zo,如等式3所示。Z(s)中的高頻極點稍后再作討論。
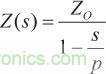 (3)
(3)圖3中的電路包含寄生電容C和跨阻Z(s)。請注意,CFA的反相輸入電容可以并入C。
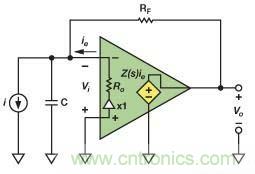
圖3. 基于實用型CFA的TIA(含寄生電容)
通過在反相輸入端執行KCL,可求得等式4。
誤差電流, ie, 為
結合等式4和等式5,可以得到如下結果,即圖3所示電路的閉環TIA增益:
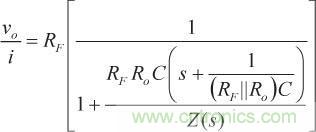 (6)
(6)等式6中的環路增益非常明顯,可通過以下等式求得
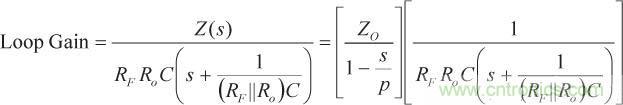 (7)
(7)環路增益含有兩個極點,一個低頻極點s = p 以及一個高頻極點
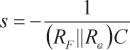
當 Ro<< RF時, RF 和 Ro的并聯結果可以通過Ro近似求出。如果在高頻極點發生的頻率下,環路增益的幅度大于0 dB,則這兩個極點會帶來穩定性問題。當Ro 和 C 較小時,寄生極點發生的頻率高于交越頻率,放大器穩定。但在多數TIA電路中,情況并非如此,因此,我們必須找到一種辦法,對反相輸入寄生電容進行補償。
添加一個反饋電容(題外話)
帶有單極點傳遞函數(如等式3所示)的CFA在任何反饋電阻值下都表現穩定,因為其反饋環路周圍的遲滯相移被限制為–90°。但實際CFA的次要極點在高頻下會帶來較大的相移遲滯,因此,為了確保穩定性,實際會對 RF 的最小值做出限制(45°一般是可接受的最小相位裕量)。此后,Z(s)將包含一個高頻極點s = pH和一個主極點 s = p。
為了確保反饋阻抗不變成零,通常建議在任何CFA電路中都不應使用反饋電容。然而,事情并非如此簡單,因為在幅度變化以外,反饋電容還會導致相移。本節將考察將一個反饋電容添加至基于CFA的TIA時產生的結果,暫且忽略寄生輸入電容。在圖2所示電路中,在反饋電阻RF上跨接一個反饋電容CF,結果形成一個極點,并在環路增益中產生一個零。ZF 定義為 RF 和 CF的并聯結果:
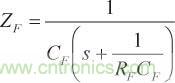 (8)
(8)如果以ZF取代等式2中的RF ,則閉環增益可表示為等式9。
 (9)
(9)此時,環路增益為
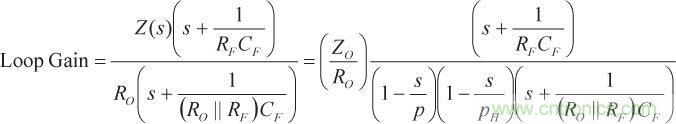 (10)
(10)環路增益有一個來自Z(s)的主極點 s = p 和一個高頻極點 s = pH 。另外,受增加的反饋電容的影響,在
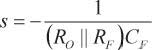
時形成一個極點,在
時產生一個零。
在波特圖中,CF 導致的零產生時的頻率低于CF導致的極點,因為零頻率表達式的分母中含有RF ,而極點頻率表達式的分母中則含有(Ro||RF)。一種基于CFA的可能TIA(含CF (等式10))的波特圖如圖4所示。
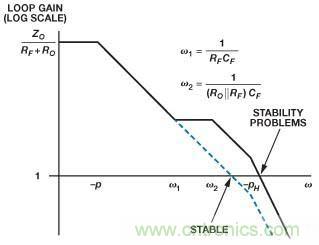
圖4. 基于CFA的TIA(含反饋)的波特圖
隨著頻率的增加,零會導致幅度不斷提高,相移不斷加大,從穩定性角度來看,在某些情況下,這可能是一件好事。但在圖4所示系統中,零出現在環路增益跨過0 dB之處,而pH 下的極點則在跨交越點–40 dB/十倍頻程時導致幅度漸近線下降。藍色虛線表示不含CF的環路增益,采用的是等式2以及雙極點版本的Z(s)(見等式11)。
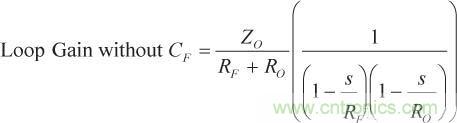 (11)
(11)F圖4表明,當無CF時,放大器表現穩定,但在添加CF之后,則會產生穩定性問題。圖4中的坐標圖并不完全排除反饋電容的使用,因為該特定Z(s)并不代表所有CFA,而且未使用實際電阻和電容值;盡管如此,圖中確實表明,高頻極點會限制可以安全應用的反饋電容。圖4同時表明,可以向一個帶單極點傳遞函數的假想CFA安全添加任意量的反饋電容,而添加反饋電容會增加其閉環帶寬。
使用CF導致的零抵銷寄生電容導致的極點
以上簡要介紹了向CFA添加CF產生的影響,從中可以看出,可以安全使用CF 來補償輸入電流源的寄生分流電容。
圖3所示電路的閉環增益表示為等式6。為了厘清添加反饋電容對該電路的影響,可用ZF取代等式6中的RF ,與推導等式9的方法相似,其中,ZF 由等式8定義。電路如圖5所示。
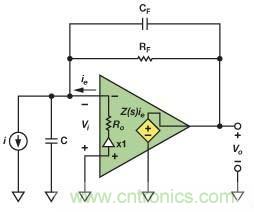
圖5. 基于實用CFA的TIA(用CF 補償寄生電容)
圖5所示電路的閉環增益可通過等式12求得:
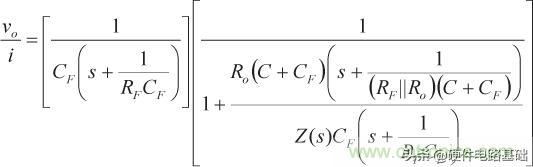 (12)
(12)根據該等式,可以算出環路增益為
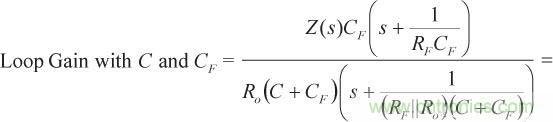
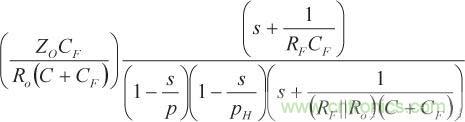 (13)
(13)等式13中,因CF導致的零與等式10中的零相同,但CF 導致的極點則從
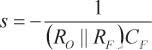
移到了
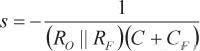
通過向CF添加C,可以移動極點位置,以匹配零的位置,從而抵銷掉輸入電流源的寄生電容C導致的極點。在等式13中,將CF和C導致的極點頻率設為因CF導致的零頻率,則得到等式14:
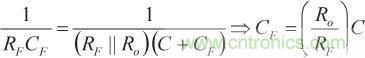 (14)
(14)等式14所示為計算CF的值的簡單公式,該值可抵銷圖5所示TIA中的寄生電容C導致的環路增益中的極點。以這種方式將極點零完美抵銷之后,環路增益會回歸最初形式,含有主極點和高頻極點,如等式11所示。至此,閉環增益可以表示為等式15。
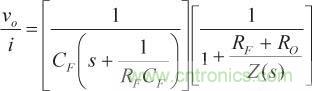 (15)
(15)在使用等式14時,遇到的主要困難是確定Ro,該值是可變的,而且CFA數據手冊中未必提供其額定值。然而,只要環路增益圖的斜率在通過0dB時合理接近–20 dB/十倍頻程,則極點-零抵銷無需如此精確。等式14表明,CF 隨 Ro 線性遞減,因為隨著 Ro 接近0,自舉發生次數會增加,其中,C完全自舉,所需 CF等于0。等式14也可表示為一種匹配時間常數形式,如RoC = RFCF。等式14的匹配時間常數形式與對VFA進行寄生求和節點電容補償時獲得的結果非常相似: RGCG = RFCF,其中 RG為VFA增益電阻,CG 為RG的交越電容,該電容一般為寄生求和節點電容。然而,獲得這種優勢是需要付出代價的。雖然添加CF可使TIA變穩定,但同時也會在
時在閉環增益中導致一個極點,如等式12和等式15所示。等式15所描述的閉環增益可以視為傳遞函數相乘的兩個級聯系統。第一個系統的傳遞函數為等式15中最左側的因子,維度為歐姆。第二個系統的傳遞函數為等式15中最右側的因子,無維度。
第二個系統的響應取決于環路增益,只要環路增益幅度在–20 dB/十倍頻程時跨過0 dB,就可以模擬為一個一階傳遞函數。基本反饋理論表明,如果達到這一滾降條件,當環路增益幅度>>1時,第二個系統的閉環增益幅度約等于單位增益,當環路增益幅度<<1時,則跟隨環路增益幅度。閉環增益中的3-dB點出現在環路增益幅度跨過0 dB時的頻率(如果斜率略快于–20 dB/十倍頻程,則在接近0-dB交越點之處,閉環響應中會出現一些峰化)。因此,在一個穩定的放大器中,第二個系統可以近似模擬為一個一階、低通濾波器,其單位增益處于通帶中,且截止頻率等于環路增益幅度跨過0 dB時的頻率。第一個系統的傳遞函數為反饋因子的倒數,其響應為簡單的一階、低通響應,直流值為RF,轉折頻率為
憑直覺可以看出,CF 導致的額外極點是意義的,因為輸出電壓是流過反饋阻抗的電流形成的,而反饋阻抗隨頻率增加而下降。當CF 的電抗等于RF的值時,會形成極點。在使用反饋電容補償、基于VFA的TIA中會發生相同的情況。不過可以略微擴大閉環帶寬,其方法是從根據等式14計算的值開始,小心地減小CF ,移出極點頻率,并縮減相位裕量,但這只能嘗試著做。
仿真數據
為了測試該結果,我們針對CFA提出了一種簡單的仿真模型,其中,Zo = 1 MΩ, p = –2π (100 kHz), pH = –2π (200 MHz), Ro = 50 Ω,且 RF = 500 Ω。環路增益的幅度則可通過以這些值代入等式11中的幅度計算得到。
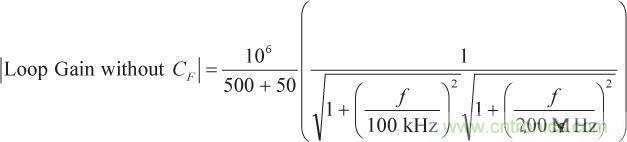 (16)
(16)結果約等于1,其中 f = 145 MHz.
145 MHz時的環路增益相移為
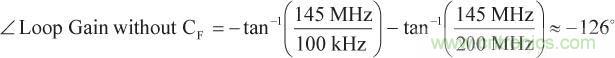 (17)
(17)結果得到大約54°的相位裕量,對于無寄生電容的基本CFA來說,這是一個不錯的起點。
圖6所示為該模型的響應仿真情況,其中,電流階躍輸入上升時間為1-ns。
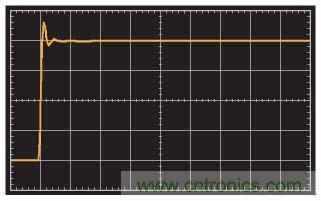
圖6. 基本TIA的階躍響應(無寄生電容)(20 ns/div)
響應非常干凈,響鈴振蕩已減至最小——為54°相位裕量條件下的應有水平。對于同一放大器,當在反相輸入端和接地之間添加一個50 pF的寄生電容時,其階躍響應如圖7所示。
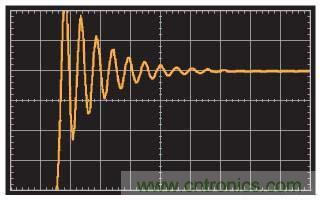
圖7. 階躍響應(反相輸入端與接地之間存在50 pF的電容)(20 ns/div)
圖7中的縱坐標與圖6相同,只是軌跡下移了一個刻度,以適應響鈴振蕩。顯然存在過多響鈴振蕩,這種放大器明顯有相位裕量問題。
放大器可以通過添加一個反饋電容(其值通過等式14決定)來實現穩定化,經計算,該電容為5 pF。圖8 所示為添加5-pF反饋電容后的結果。
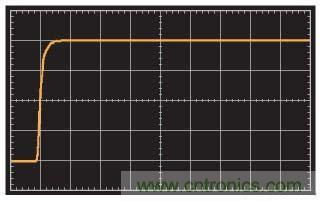
圖8. 階躍響應(以5 pF反饋電容實現極點/零抵銷)(20 ns/div)
顯然,閉環增益中的極點會對頻帶形成限制。原始放大器的環路增益0-dB交越確定為145 MHz,相當于一階系統中約1.1的時間常數,RFCF時間常數為2.5 ns(注意,0-dB交越時,環路增益幅度滾降速率略快于–20 dB/十倍頻程,因為相位裕量少于90°,但一階閉環模型是一種比較精確的近似模型)。使用由兩個級聯系統構成的上述模型,級聯系統的合并時間常數可以估算為兩個時間常數的方和根(輸入電流源10%至90%的上升時間為1ns,相當于次納秒級的有效時間常數,可忽略不計),即2.7 ns左右,似乎與圖7所示響應相符合。
將 CF 降為3 pF 可以略微減少相位裕量,加大閉環極點頻率,由此提升速度,如圖9所示。
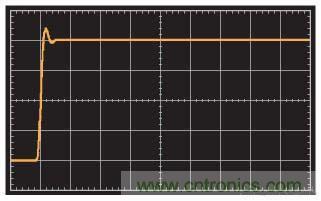
圖9. 階躍響應(帶3-pF反饋電容)(20 ns/div)
顯然,要獲得最佳的CF的值,需要進行一些實驗。諸如負載電容、電路板布局、Ro變化等因素在挑選CF時也是需要考慮的。
結論
隨著將CFA用作TIA的做法日漸盛行,有必要了解如何對CFA反相輸入端的傳感器電容進行補償,有必要了解補償機制的工作原理。本文基于經典反饋技術,提出了一種簡便辦法,即將一個反饋電容與反饋電阻并聯起來,對反相輸入電容進行補償。反饋電容會在閉環響應中導致一個無用極點,但可以基于計算所得值對電容的值進行調整,以減少極點對頻帶的限制作用。






