線圈匝數的計算是開關電源設計的關鍵,而單激式和雙擊式開關電源又各不相同。本講主要分析在不同類型電壓脈沖輸入下初級線圈電場、磁場的變化,電磁能量轉換的過程,實際設計中應當注意的問題,推導出線圈匝數的計算通式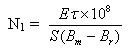 。
。
雙激式開關電源變壓器伏秒容量與初級線圈匝數的計算
在圖2-1中,當有直流脈沖電壓輸入變壓器初級線圈a、b兩端時,在變壓器初級線圈中就有勵磁電流流過,勵磁電流會在變壓器鐵芯中產生磁通![]() ,同時在變壓器初級線圈兩端還會產生反電動勢;反電動勢電壓的幅度與輸入電壓的幅度相等,但方向相反。
,同時在變壓器初級線圈兩端還會產生反電動勢;反電動勢電壓的幅度與輸入電壓的幅度相等,但方向相反。
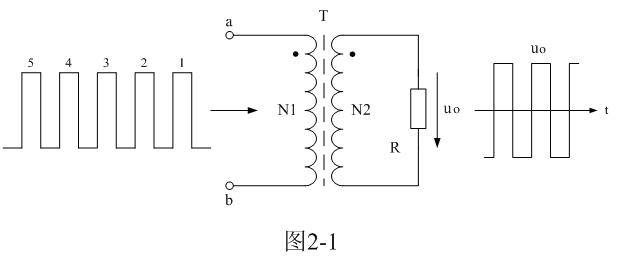
因此,根據電磁感應定律,變壓器鐵芯中磁通 的變化過程由下式決定:
的變化過程由下式決定:

上面(2-13)、(2-14)、(2-15)式中,US為變壓器的伏秒容量,US = E×τ ,即:伏秒容量等于輸入脈沖電壓幅度與脈沖寬度的乘積,單位為伏秒,E為輸入脈沖電壓的幅度,單位為伏,τ為脈沖寬度,單位為秒;Δ 為磁通增量,單位為麥克斯韋(Mx),Δ
為磁通增量,單位為麥克斯韋(Mx),Δ  = S×ΔB ;ΔB磁通密度增量,ΔB = Bm-Br ,單位為高斯(Gs);S為鐵芯的截面積,單位為平方厘米;N1為變壓器初級線圈N1繞組的匝數,K為比例常數。[page]
= S×ΔB ;ΔB磁通密度增量,ΔB = Bm-Br ,單位為高斯(Gs);S為鐵芯的截面積,單位為平方厘米;N1為變壓器初級線圈N1繞組的匝數,K為比例常數。[page]
伏秒容量表示一個變壓器能夠承受多高的輸入電壓和多長時間的沖擊。因此,變壓器的伏秒容量US越大,表示流過變壓器初級線圈的勵磁電流就越小。一般變壓器的勵磁電流都是不提供功率輸出的,只有反激式開關電源是例外,因此,在正激式變壓器開關電源或雙激式變壓器開關電源中,勵磁電流越小,表示開關電源的工作效率越高。
在一定的變壓器伏秒容量條件下,輸入電壓越高,變壓器能夠承受沖擊的時間就越短,反之,輸入電壓越低,變壓器能夠承受沖擊的時間就越長;而在一定的工作電壓條件下,變壓器的伏秒容量越大,變壓器的鐵芯中的磁通密度就越低,變壓器鐵芯就更不容易飽和。變壓器的伏秒容量與變壓器的體積以及功率基本無關,只與磁通的變化量大小有關。
如果我們對(2-15)式稍微進行變換,就可以得到單激式開關電源變壓器初級線圈匝數計算公式:

(2-16)式就是計算單激式開關電源變壓器初級線圈N1繞組匝數的公式。式中,N1為變壓器初級線圈N1繞組的最少匝數,S為變壓器鐵芯的導磁面積(單位:平方厘米),Bm為變壓器鐵芯的最大磁通密度(單位:高斯),Br為變壓器鐵芯的剩余磁通密度(單位:高斯),τ為脈沖寬度,或電源開關管導通時間的寬度(單位:秒),E為脈沖電壓幅度,即開關電源的工作電壓幅度,單位為伏。
(2-16)式中的指數108在數值上正好等于(2-13)、(2-14)、(2-15)式中的比例系數K,因此,選用不同單位制,比例系數K的值就會不一樣;這里選用CGS單位制,即:長度為厘米(cm),磁通密度為高斯(Gs),磁通單位為麥克斯韋(Mx)。
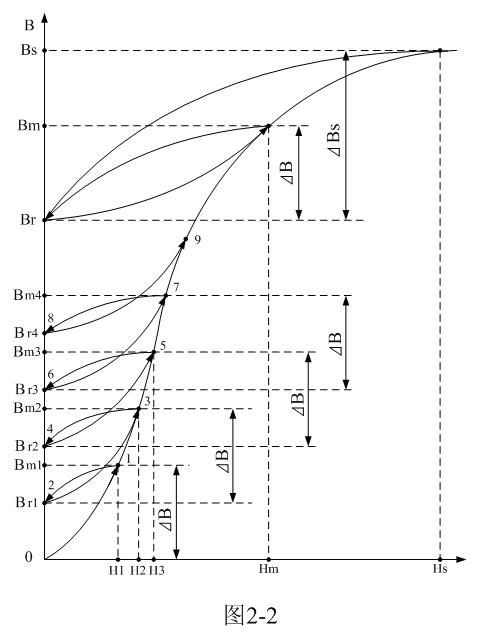
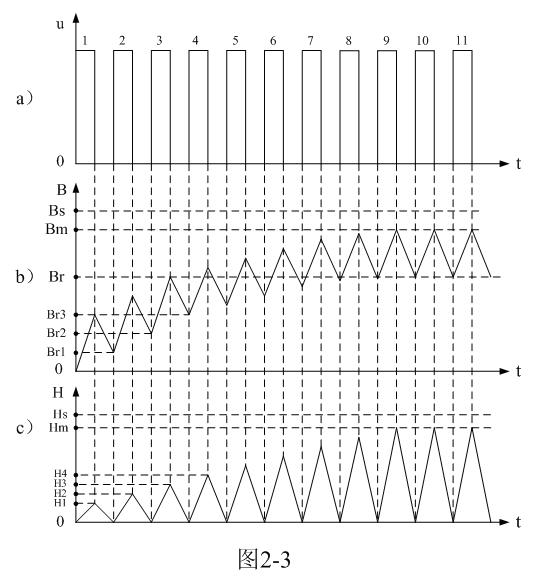
從圖2-2和圖2-3還可以看出,直接采用圖2-2和圖2-3的參數來設計單激式開關電源變壓器,在實際應用中是沒有太大價值的。因為,普通變壓器鐵芯材料的最大磁通密度Bm的值都不大,大約在3000~5000高斯之間,剩余磁通密度Br一般卻高達最大磁通密度Bm的80%以上。[page]
因此,實際可應用的磁通密度增量ΔB一般都很小,大約只有500高斯左右,一般不會超過1000高斯。為了增大磁通密度增量ΔB,一般都需要在變壓器鐵芯中留出一定長度的氣隙,以降低剩余磁通密度Br的數值。
由(2-13)和(2-14)式可以知道,盡管磁化曲線不是線性的,但當輸入電壓為方波時,流過變壓器初級線圈勵磁電流所產生的磁通還是按線性規律增長的;而流過變壓器初級線圈勵磁電流以及磁場強度卻不一定是按線性規律增長,正因為如此,才使得(2-13)和(2-14)式中出現一個比例常數K 。
也就是說,當我們把(2-13)、(2-14)、(2-15)式中的系數K作為一個比例常數看待時,同時也就意味著,我們已經把變壓器鐵芯的導磁率也當成了一個常數看待了,但由于變壓器鐵芯導磁率的非線性以及勵磁電流的非線性,兩個非線性參數互相補償,才使得變壓器鐵芯中的磁通按線性規律變化。因此,在變壓器鐵芯將要接近飽和的時候,變壓器初級線圈中的勵磁電流是非常大的。
在單激變壓器開關電源中,雖然流過變壓器初級線圈中的電流所產生的磁通是按線性規律上升的,但變壓器鐵芯產生退磁時,磁通的變化并不一定是按線性規律下降的。這個問題在第一章的內容中已經基本作了解釋。當直流脈沖電壓過后,變壓器次級線圈中產生的是反激式電壓輸出,在純電阻負載中,其輸出電壓一般是一個按指數規律下降的電壓脈沖,因此,其對應的磁通增量就不可能是按線性規律變化,而應該也是按指數規律變化的,不過后一種指數規律正好是對前一種指數規律進行積分的結果。這種對應關系從(2-13)和(2-14)式中也很容易可以看得出來。
這里順便指出:單激式變壓器開關電源中,對變壓器鐵芯產生磁化作用的只有流過變壓器初級線圈的勵磁電流,因此,勵磁電流也稱磁化電流;而對變壓器鐵芯產生退磁作用的是變壓器初、次級線圈產生的反電動勢,以及由反電動勢產生的電流,即:反激輸出電壓和電流;而正激輸出電壓和電流對變壓器鐵芯的磁化和退磁不起作用。
因為,勵磁電流雖然會產生正激電壓,但不能提供正激電流輸出,這相當于變壓器次級線圈處于開路時的情況一樣;當變壓器次級線圈有正激電流輸出時,在變壓器初級線圈中也相應要增加一個電流,這個電流是在原勵磁電流的基礎上相應增加的;這個新增電流產生的磁通與正激輸出電流產生的磁通,在數值上完全相等,但方向相反,兩者互相抵消,即它們對磁化和退磁都不起作用。[page]
雙激式開關電源變壓器伏秒容量與初級線圈匝數的計算
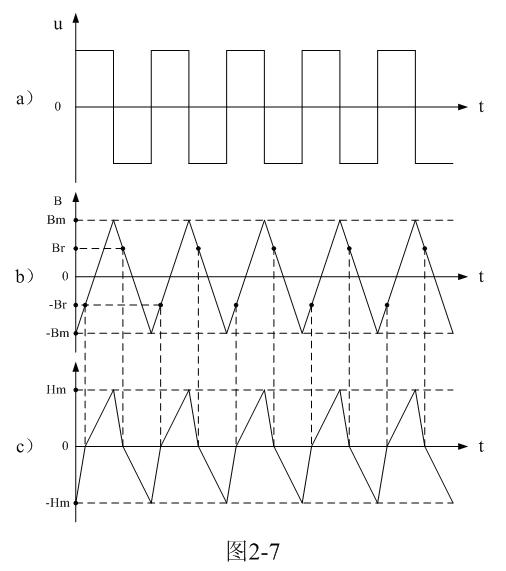
在圖2-7中,對于雙激式開關電源變壓器,每輸入一個交流脈沖電壓,除了第一個輸入脈沖的磁通密度變化范圍是從0到最大值Bm以外,其余輸入脈沖,磁通密度的變化范圍都是從負的最大值-Bm到正的最大值Bm ,或從正的最大值Bm到負的最大值-Bm ,即:每輸入一個交流脈沖電壓,磁通密度的增量ΔB都是最大磁通密度Bm的2倍(2Bm)。因此,把這個結果代入(2-13)和(2-14)式,即可求得:

(2-17)和(2-18)式,就是計算雙激式開關電源變壓器初級線圈N1繞組匝數的公式。式中,N1為變壓器初級線圈N1繞組的最少匝數,S為變壓器鐵芯的導磁面積(單位:平方厘米),Bm為變壓器鐵芯的最大磁通密度(單位:高斯),τ為脈沖寬度,或電源開關管導通時間的寬度(單位:秒),E為脈沖電壓的幅度,即開關電源的工作電壓幅度,單位為伏,F為開關電源的工作頻率,單位赫芝。
同樣,我們把(2-17)式中的輸入脈沖電壓幅度E與脈沖寬度τ的乘積定義為變壓器的伏秒容量,用US來表示(單位:伏秒),即:US = E×τ 。
這里還需指出,使用(2-17)和(2-18)式計算雙激式開關電源變壓器初級線圈N1繞組的匝數是有條件的,條件就是輸入交流脈沖電壓正、負半周的伏秒容量Us必須相等。如果不相等(2-17)和(2-18)式中的磁通密度增量ΔB就不能用2Bm來表示,而應該用Bm和-Bm這兩個實際變量的差值,即:ΔB = Bm-(-Bm),這里姑且把Bm和-Bm都看成是變量更合適。
把(2-17)式和(2-18)式與(2-16)式進行對比很容易看出,在變壓器鐵芯的導磁面積以及輸入電壓幅度完全相等的條件下,雙激式開關電源變壓器鐵芯中的磁通密度變化范圍要比單激式開關電源變壓器鐵芯中的磁通密度變化范圍大很多;或者在伏秒容量完全相等的條件下,雙激式開關電源變壓器初級線圈的匝數要比單激式開關電源變壓器初級線圈的匝數少很多。因此,用于雙激式開關電源變壓器,一般都不需要在其變壓器鐵芯中留氣隙。
在(2-17)和(2-18)式中,對于大功率雙激式開關電源變壓器的鐵芯,其最大磁通密度Bm的取值一般不要超過3000高斯。如果Bm值取得過高,當開關器件偶然發生誤觸發,使圖2-7中的相位出錯時,很容易使變壓器鐵芯出現磁飽和,致使開關電源工作電流過大而損壞。
各種波形電源變壓器初級線圈匝數的計算
(2-18)式雖然是用于計算雙激式開關電源變壓器初級線圈N1繞組匝數的公式,但只需把式中的某個別參數稍微進行變換或修改,同樣可以用于計算其它波形電源變壓器初級線圈匝數的公式。
[page]
這里,我們先來推導用于計算正弦波電源變壓器初級線圈匝數的公式。方法如圖2-8所示,先求正弦電壓的半周平均值Ua,因為正弦電壓的半周平均值Ua正好等于方波電壓的幅值E,因此,只需把正弦電壓的半周平均值代入(2-18)式,即可得到計算正弦波電源變壓器初級線圈匝數的公式。
但正弦電壓的半周平均值Ua一般很少人使用,因此,還需要把正弦電壓的半周平均值Ua再轉換成正弦電壓的有效值U;由于正弦電壓的有效值U等與正弦電壓半周平均值Ua的1.11倍,即:U = 1.11Ua 。由此求得正弦波電源變壓器初級線圈匝數的計算公式為:

(2-19)式為計算正弦波電源變壓器初級線圈N1繞組匝數的公式。式中,N1為變壓器初級線圈N1繞組的最少匝數,S為變壓器鐵芯的導磁面積(單位:平方厘米),Bm為變壓器鐵芯的最大磁通密度(單位:高斯),U為正弦波輸入電壓有效值,單位為伏,F為正弦波的頻率,單位赫芝。
這種計算方法,對于非正弦波同樣有效。圖2-9是一個正、負脈沖幅度以及脈沖寬度均不相等的交流脈沖波形,我們同樣可以用分別計算它們正、負半周平均值Ua、-Ua的方法,然后用平均值Ua替代(2-17)或(2-18)式中的矩形脈沖幅度E 。
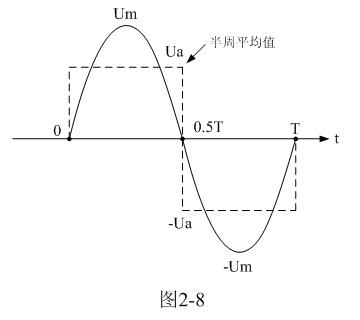
當然圖2-9中的條件是正、負脈沖的伏秒容量均應相等,如果不相等,可采取兼顧單、雙激開關電源變壓器初級線圈匝數的計算方法,即:兩種方法同時考慮,根據偏重取折中。
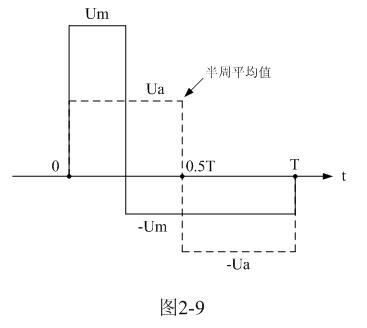
各種波形的半周平均值Ua由下式求得:
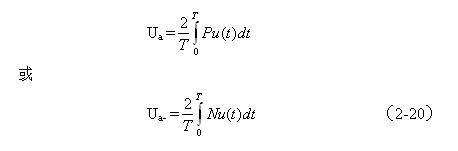
(2-19)、(2-20)式中,Ua和Ua-分別為各種波形的正、負半周平均值,Pu(t)和Nu(t)分別為各種波形的正波形函數(正半周)和負波形函數(負半周),T為種波形的周期。大部分交流電壓波形,其正、負半周平均值的絕對值都相等,但符號相反。
順便說明,這里的半周平均值,并不是一般意義上的正、負半周波形完全對稱交流電壓正半周,或負半周的平均值,這里的半周平均值是泛指整個周期中的正半波電壓或負半波電壓在半個周時間內的平均值。如圖2-9所示。另外,(2-19)、(2-20)式中的半周平均值Ua和Ua-與第一章中(1-73)、(1-74)、(1-75)式定義的半波平均值Upa和Upa-也有一點差別,Ua和Ua-與Upa和Upa-的差別,主要是在分母上。








