中心議題:
- PFC整流器系統結構和狀態方程
- 不對稱電壓對輸入電流的影響
- PFC整流器改進的控制策略
本文分析了基于單周期控制技術的雙并聯升壓型三相 PFC 整流器在電網電壓不對稱時輸入電流跟蹤輸入電壓不良的問題,提出了一種有效的改進措施,通過計算相電壓不對稱系數,對占空比計算公式進行修正,以消除不對稱電壓對輸入電流波形跟蹤不良的影響,使每相電流均和各自的電壓同相,從而實現單位功率因數和低電流畸變。在任意時刻,該整流器只需要兩個開關管工作在高頻狀態,從而使開關管的總體損耗程度進一步降低。最后通過硬件實驗驗證了該控制策略的正確性。
1 引言
近十幾年來, 隨著電力電子技術的發展,許多大容量電機調速系統、家用電器等設備的電力供應都需要對交流電網進行各種AC/DC 或AC/DC/AC的變換。而使用傳統的二極管或晶閘管為功率開關管的非線性變流裝置進行的電源變換將會在電網中產生各種電流諧波,嚴重干擾了其他電氣設備的正常工作,增加了功耗,同時使電網功率因數大大降低減少了電網的有效傳送容量。為此,國際電工委員會的IEC1000-3-3 和IEC519 對整流設備的電流諧波和電磁干擾品質進行了嚴格。規定為了達到這些要求,各國學者對功率因數校正PowerFactor Correction, PFC 技術進行了深入研究,并取得了一系列成果。現在,PFC 技術已經成為電力電子學科的重要研究方向之一。目前,單相PFC 技術在電路拓撲和控制策略等方面已日趨成熟,但是三相PFC 整流器由于各相電流互相耦合,需要較為復雜的控制算法才能實現,而且它的輸出功率大,對電網的污染更加嚴重,因此三相功率因數校正技術的研究和實現具有重要意義已成為近年來的研究熱點。
三相 PFC 整流器的控制主要有半解耦和全解耦兩大類,主流的控制算法有基于 d-q 解耦的空間矢量調制,遲滯比較算法和單周期控制等。空間矢量調制要求對輸入電壓進行d-q 解耦控制算法復雜,需采用數字信號處理器DSP 才能實現。而遲滯比較算法的開關頻率不恒定,對輸入和輸出的干擾比較大,需要比較大的電感和電容作為濾波元件。
基于單周期控制的三相PFC 整流器進行了比較深入的研究,該控制器是一種不需要乘法器的新穎控制器,只需對輸入電流進行簡單的積分和加減運算,并和參考電壓直接進行比較即能實現恒調制頻率的開關元件控制波形。該控制器同時具有調制和控制的雙重功能,無論在穩態或暫態情況下,在控制周期內受控的輸入電流平均值均能恰好正比于控制參考信號,具有動態響應快、開關頻率穩定、魯棒性強、易于實現等優點。因而成為三相PFC 整流器的主流控制算法。但是在三相輸入電壓對稱的情況下進行研究而在三相電壓不對稱的情況下,輸入電流雖然仍能保持低的電流畸變,但輸入電流將與輸入電壓產生相移,未能達到單位功率因數的控制目標。本文在分析該控制器產生相移原因的基礎上,提出改進的控制策略,使該控制器在三相輸入電壓不對稱的情況下,各相輸入電流仍能和輸入電壓保持同相,實現單位功率因數和低電流諧波。
2 系統結構和狀態方程
圖 1 給出了雙并聯升壓型三相整流器的主電路原理圖。另外,圖2 還給出了輸入電壓b 相幅值減少20% ,c 相相位滯后30 °時三相電壓的波形,并按虛線劃分為六個區間。須注意的是,輸入電壓不對稱的情況不同,其分區點也可能不同,分區點由各相非零序電壓瞬時最大幅度區分點所確定。依據六階段PWM 控制技術原理,三相整流器可以通過在線性周期的每一區間內控制兩個開關的通斷來實現單位功率因數。
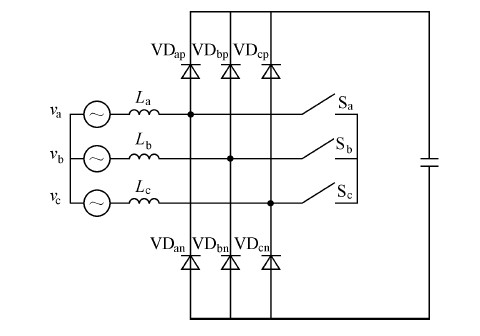
圖1 雙并聯升壓型三相整流器主電路拓撲圖
[page]
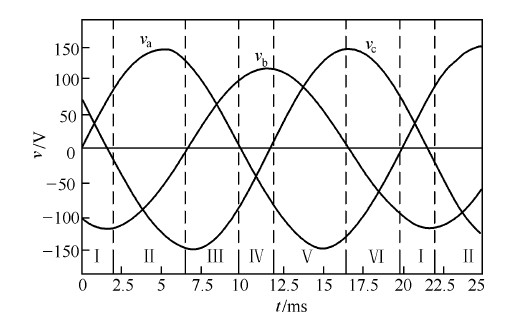
圖2 b相幅值減小20% ,c相滯后30 ° 時三相電壓的波形圖
在開始詳細分析前,假設輸入電壓為正弦波,三相電路參數對稱,功率元器件的正向阻抗和其他寄生參數忽略不計。以圖1 的主電路輸入如圖2 所示的電壓為例,在區間I 內,開關Sb 一直處于導通狀態,只對開關Sa 和Sc 進行控制,此時三相整流器可以解耦為如圖3 所示的雙并聯升壓型拓撲結構。
圖中 Vp 、Vn 為不同區間所對應的電壓,Lp、 Ln 和Lt 為不同區間所對應的電感,Tp、 Tn 為不同區間所對應的主控開關,dp 、dn 為主控開關的占空比。由于PWM 開關頻率遠高于電網頻率,因此,在一個開關周期內,各電感的電壓平均值為零,運用回路電流法和節點電壓法對各種開關狀態進行分,析可得出:
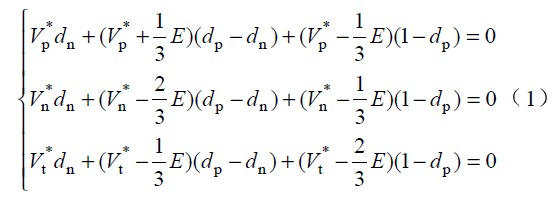
和
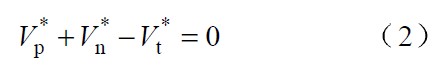
從而推導出
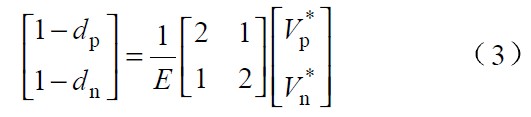
其中
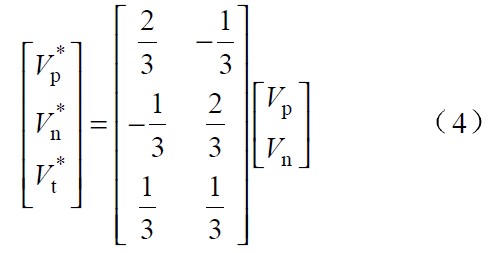
[page]
可以證明,式1 在任意區間的兩種開關順序都成立,并且只要電路工作在連續導通的模式,該等式即能準確反映出穩態電路的輸入電壓、輸出電壓和占空比三者之間的固定關系,與所采用的控制方案無關。因此式1 即為該整流器的狀態方程。
3 不對稱電壓對輸入電流的影響
依據式4 構建三相PFC 整流器,并根據三相電壓對稱和實現單位功率因數的目標而令va = Reia ,vb = Reib和vc = Reic,然后根據va+vb+vc=0和ia+ib+ic=0 的約束條件得知只要控制其中兩相電流跟蹤對應相的電壓,就可以使另外一相電流也跟蹤該相電壓。由此推算出實現單位功率因數的占空比計算公式:
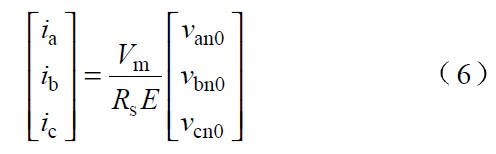
當輸入電壓不對稱時,va+vb+vc=0 不一定成立,如果仍然按照式5 作為單周期控制的占空比函數,此時各相電流為:
其中:
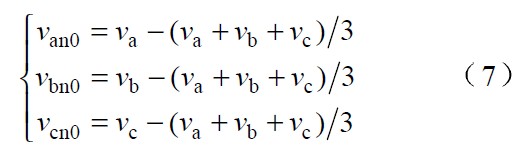
即 van0, vbn0 和vcn0 分別為各相電壓不含零序電壓的部分。由式(6) 和式(7 )可知,各相電流仍能保持低電流畸變。但若(va+vb+vc)/3≠0, 輸入電流和輸入電壓會存在一個相位差,從而導致系統不能實現單位功率因數。為使系統仍能實現單位功率因數的目標,必須改進系統的控制策略。
4 改進的控制策略
4.1 相電壓不對稱系數的計算
三相輸入電壓不對稱時,假設各相電流跟蹤各自的相電壓此,時可令從輸入端看進去各相對中線的等效電阻為Ra ,Rb 和Rc 。因系統采用三相三線制在任意時刻均有:
![]()
故對任意時刻 t0 t1 t2, ……,tn 有:
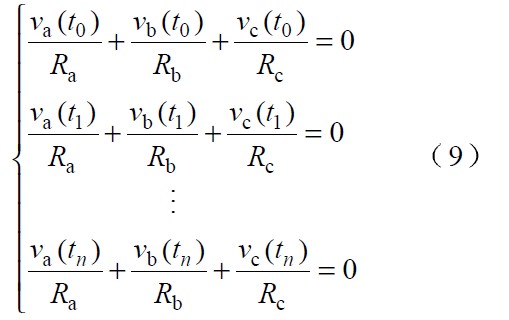
由于電網電壓可能存在各種干擾,為使計算結果盡可能精確,可將一個或幾個周期內的n 個采樣電壓分為多組,取其中的兩組來計算相電壓不對稱系數。對式(9) 按該兩組相加,可得:
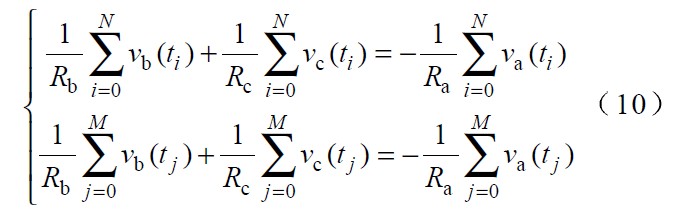
[page]
由此得:

式 (11 )為相電壓不對稱系數的計算公式,其中λa ,λb 和λc 為相電壓不對稱系數,Re 為標準等效電阻。可見,當電網電壓不對稱時,為使各相電流仍能正確跟蹤對應相電壓,各相等效電阻值是不同的。特殊地,如果三相電壓對稱,λa=λb=λc =1 ,則Ra=Rb=Rc=Re.
4.2 PFC 控制策略
由于三相輸入電壓不對稱,為達到單位功率因數,可令各相電流都跟蹤各自相電壓,即:
![]()
根據式 (3 ),以區間I 為例,可以通過控制開關 Tp 、Tn 使電感電流iLb iLc 對應 V *p和 V *n相應的變化來實現。由于在I 區間內有:
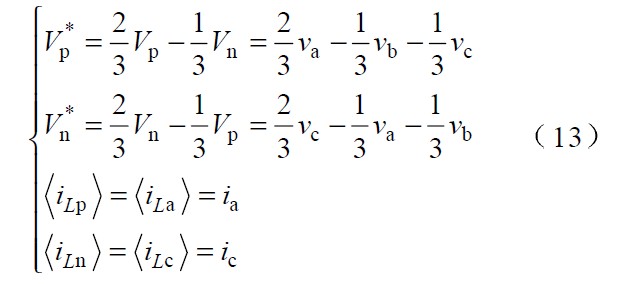
把式(8 )式(11 )和式(12 )代入式(13) 得:
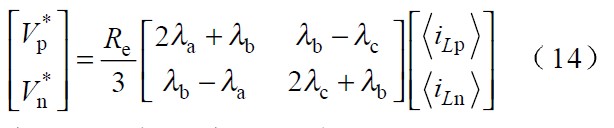
把式(14 )代入式(3 )得:
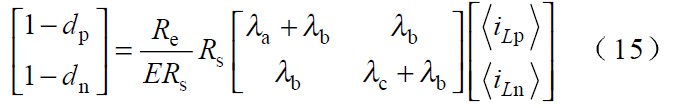
令:
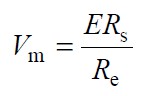
[page]
式中--Rs 等效電流監測電阻。Vm --反饋電壓環誤差補償器的輸出電壓。
此時式(15 )可表示為:
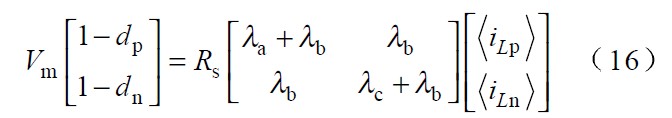
采用相同的分析方法所有區間內的占空比公式可統一表示成:
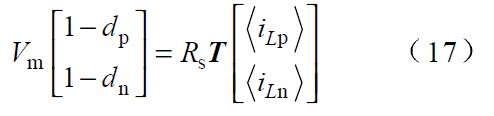
其中矩陣 T 在不同區間的取值如表1。
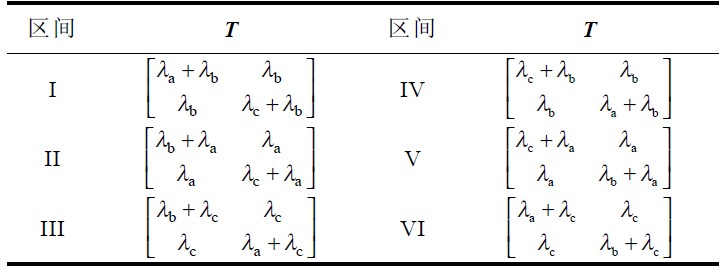
表 1 矩陣 T 在不同區間的取值對照表
由式(17 )可知,如果控制開關Tp 和Tn, 使開關占空比dp 和dn 滿足該式的線性組合,就可以實現三相PFC. 因此,式(17 )是改進后實現單位功率因數的關鍵函數。當輸入電壓對稱時,λa=λb=λc=1 ,式(17 )即簡化為式(5)。
4.3 改進策略條件下各相電流幅值分配比例
以下詳細分析按改進策略控制整流器時各相電流幅值分配比例的情況。不失一般性,假設三相輸入電壓為:
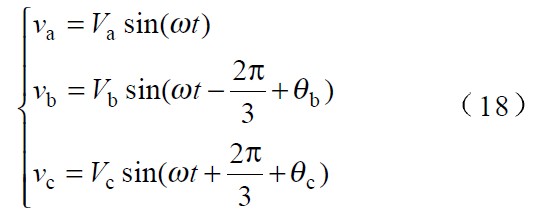
由于改進策略的控制目標為各相輸入電流跟蹤對應相電壓,因而各相輸入電流可表示成:

將式(19 )代入式(8 )可得:

由式(20 )可得出以下三點結論:
①各相電流幅值的分配比例只與輸入相電壓的偏移角度有關,與各相輸入電壓的幅值大小無關。并且在一定范圍內,偏移角度越大,該相的電流幅值分配比例就越大。
②若輸入相電壓相位對稱,即θb=θc=0 ,輸入相電流對稱。
③輸入缺相時,由于所缺相的電流必為0 ,由式(8 )和式(20 )可知,其他兩相的電流也必為0 .此時,整流器不能正常工作。
[page]
5 實驗研究
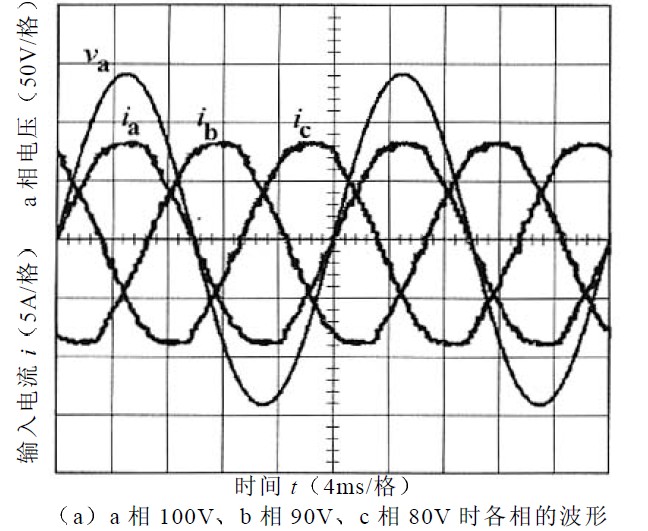
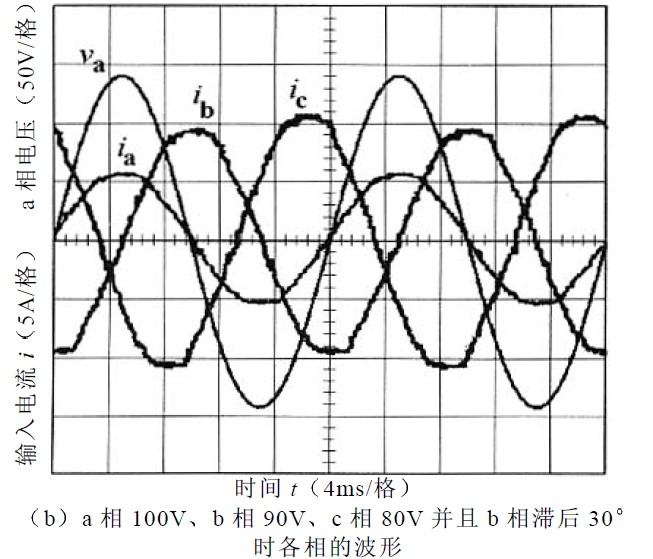
為驗證以上理論分析的正確性,根據圖1 所示的主電路拓撲結構搭建一個2kW 的三相PFC 實驗系統。該實驗系統采用TI 公司的TMS 320LF2407為整個系統的核心控制模塊,實現區間判定、相電壓不對稱系數計算、占空比計算、PWM 調制等控制功能。系統的主要參數為:輸入電感La=Lb=Lc=10mH ,輸出電容C0=470μF ,主開關元件采用MTY25N60E, 整流二極管采用MUR3080 ;系統的輸出為直流400V ;開關頻率為5kHz ;負載電阻為;輸出功率為1.6kW ;實驗的輸入電流和a 相電壓如圖4 所示,示波器電壓波形為50V/格,電流波形為 5A/格;圖4a、 圖4b 的時間t 為4ms/格;圖4d的時間t 為100ms/格,對比圖4 電流波形可以發現:
[page]

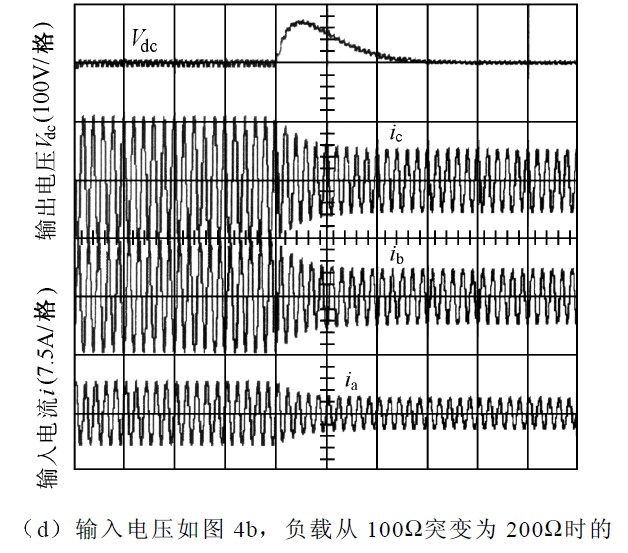
圖4 實驗輸入電壓電流波形圖
①只要三相電壓相位對稱,輸入電流就對稱。
②相位不對稱時,各相的電流幅值差別就比較大。
③單位功率因數控制方法在輸入電壓不對稱時輸入電流會發生相移,實現不了單位功率因數。
④從圖4d 可以看出系統動態響應時間約為4 個電源周期,這和采用文獻[1]算法的系統動態響應時間大致相當。對圖4a 和圖4b 的各電流波形進行傅里葉分析,各相的THD 均在3%以下,功率因數為99.98%左右,進一步驗證了改進控制策略的正確性在輸入對稱或不對稱情況下,各相電流都能很好地跟蹤相電壓,實現了單位功率因數。
6 結論
本文分析了基于單周期控制技術的雙并聯升壓型三相PFC 整流器在輸入電壓不對稱情況下輸入電流跟蹤輸入電壓不良的問題,并給出了改進的控制算法。該算法通過一個或幾個周期的采樣電壓計算出輸入電網電壓的相電壓不對稱系數,并由此修正單位功率因數的計算公式,使各相輸入電流仍能很好地跟蹤各相電壓,實現單位功率因數和低電流畸變。與其他類型的三相PFC 整流器比較起來,本控制器有工作可靠、控制方案簡單、只需要進行簡單運算等優點,并且在輸入電壓不對稱的情況下仍能實現單位功率因數和很低的電流畸變。隨著DSP 技術和工藝的迅猛發展,高性能DSP 硬件成本越來越低,采用高性能DSP 實現本控制器,其電路復雜度將大大降低,具有良好的應用前景。







