- 開關電源的小信號模型及環路設計
- 平均電流模式控制
- 采用變通的電流模式控制方法
- 采用平均狀態方程的方法
- 環路設計
1引言
設計一個具有良好動態和靜態性能的開關電源時,控制環路的設計是很重要的一個部分。而環路的設計與主電路的拓撲和參數有極大關系。為了進行穩定性分析,有必要建立開關電源完整的小信號數學模型。在頻域模型下,波特圖提供了一種簡單方便的工程分析方法,可用來進行環路增益的計算和穩定性分析。由于開關電源本質上是一個非線性的控制對象,因此,用解析的辦法建模只能近似建立其在穩態時的小信號擾動模型,而用該模型來解釋大范圍的擾動(例如啟動過程和負載劇烈變化過程)并不完全準確。好在開關電源一般工作在穩態,實踐表明,依據小信號擾動模型設計出的控制電路,配合軟啟動電路、限流電路、鉗位電路和其他輔助部分后,完全能使開關電源的性能滿足要求。開關電源一般采用Buck電路,工作在定頻PWM控制方式,本文以此為基礎進行分析。采用其他拓撲的開關電源分析方法類似。
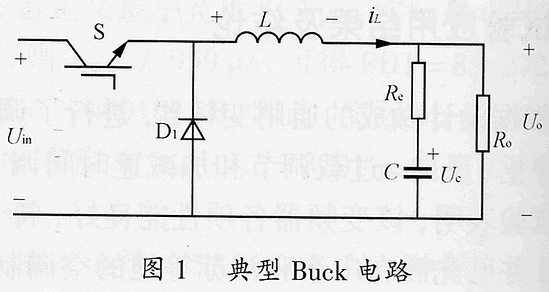
S導通時,對電感列狀態方程有L(dil/dt)=Uin-Uo (1)S斷開,D1續流導通時,狀態方程變為L(dil/dt)=-Uo ( 2)
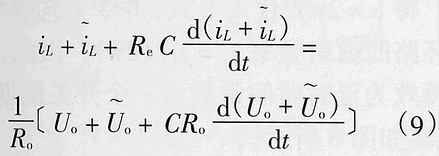
占空比為D時,一個開關周期過程中,式(1)及式(2)分別持續了DTs和(1-D)Ts的時間(Ts為開關周期),因此,一個周期內電感的平均狀態方程為
L(dil/dt)=D(Uin-Uo)+(1-D)(-Uo)=DUin-Uo (3)
穩態時,=0,則DUin=Uo。這說明穩態時輸出電壓是一個常數,其大小與占空比D和輸入電壓Uin成正比。
由于電路各狀態變量總是圍繞穩態值波動,因此,由式(3)得
L[d(il il'''''''')/dt]=(D+d)(Uin+Uin'''''''')-(Uo+Uo'''''''') (4)
[page]
L(dil''''''''/dt)=DUin''''''''+dUin-Uo'''''''' (5)
由圖1,又有
iL=C(duc/dt)+Uo/R0 (6)
Uo=Uc+ReC(duc/dt) (7)
式(6)及式(7)不論電路工作在哪種狀態均成立。由式(6)及式(7)可得
iL+ReC(dil/dt)=1/Ro(Uo+CRo(duo/dt)) (8)
式(8)的推導中假設Re<
式(9)減式(8)得
iL ReC(dil/dt)=1/Ro(Uo+CRo(dUo/dt)) (10)
將式(10)進行拉氏變換得
iL(s)=(Uo(s)/Ro)·[(1 sCRo)/(1 sCRe)] (11)
(s)=(11)一般認為在開關頻率的頻帶范圍內輸入電壓是恒定的,即可假設=0并將其代入式(5),將式(5)進行拉氏變換得
sLiL''''''''(s)=d(s)Uin-Uo''''''''(s) (12)
由式(11),式(12)得
Uo''''''''(s)/d(s)=Uin[(1 sCRe)/(s2LC s(ReC L/Ro) 1] (13)
iL''''''''(s)/d(s)=[(1 sCRo)/s2LC s(ReC L/Ro) 1]·Uin/Ro (14)
式(13),式(14)便為Buck電路在電感電流連續時的控制-輸出小信號傳遞函數。
式(9)減式(8)得
iL ReC(dil/dt)=1/Ro(Uo+CRo(dUo/dt)) (10)
將式(10)進行拉氏變換得
iL(s)=(Uo(s)/Ro)·[(1 sCRo)/(1 sCRe)] (11)
(s)=(11)一般認為在開關頻率的頻帶范圍內輸入電壓是恒定的,即可假設=0并將其代入式(5),將式(5)進行拉氏變換得
sLiL''''''''(s)=d(s)Uin-Uo''''''''(s) (12)
由式(11),式(12)得
Uo''''''''(s)/d(s)=Uin[(1 sCRe)/(s2LC s(ReC L/Ro) 1] (13)
iL''''''''(s)/d(s)=[(1 sCRo)/s2LC s(ReC L/Ro) 1]·Uin/Ro (14)
式(13),式(14)便為Buck電路在電感電流連續時的控制-輸出小信號傳遞函數。
2 電壓模式控制(VMC)
電壓模式控制方法僅采用單電壓環進行校正,比較簡單,容易實現,可以滿足大多數情況下的性能要求,如圖2所示。
圖2中,當電壓誤差放大器(E/A)增益較低、帶寬很窄時,Vc波形近似直流電平,并有
D=Vc/Vs (15)
d=Vc''''''''/Vs (16)
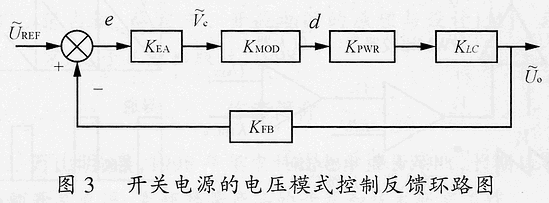
式(16)為式(15)的小信號波動方程。整個電路的環路結構如圖3所示。圖3沒有考慮輸入電壓的變化,即假設Uin=0。圖3中,(一般為0)及分別為電壓給定與電壓輸出的小信號波動;
KFB=UREF/Uo,為反饋系數;誤差e為輸出采樣值偏離穩態點的波動值,經電壓誤差放大器KEA放大后,得;KMOD為脈沖寬度調制器增益,KMOD=d/=1/Vs;KPWR為主電路增益,KPWR=/d=Uin;KLC為輸出濾波器傳遞函數,KLC=(1 sCRe)/[S2LC s(ReC L/Ro) 1]。
在已知環路其他部分的傳遞函數表達式后,即可設計電壓誤差放大器了。由于KLC提供了一個零點和兩個諧振極點,因此,一般將E/A設計成PI調節器即可,KEA=KP(1+ωz/s)。其中ωz用于消除穩態誤差,一般取為KLC零極點的1/10以下;KP用于使剪切頻率處的開環增益以-20dB/十倍頻穿越0dB線,相角裕量略小于90°。
VMC方法有以下缺點:
1)沒有可預測輸入電壓影響的電壓前饋機制,對瞬變的輸入電壓響應較慢,需要很高的環路增益;
2)對由L和C產生的二階極點(產生180°的相移)沒有構成補償,動態響應較慢。
VMC的缺點可用下面將要介紹的CMC方法克服。
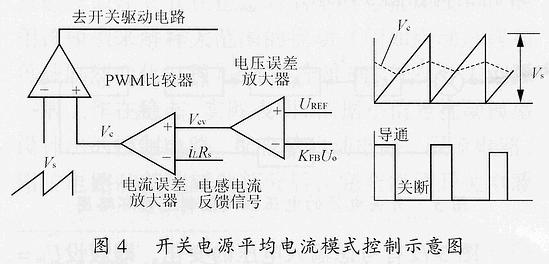
3 平均電流模式控制(AverageCMC)
平均電流模式控制含有電壓外環和電流內環兩個環路,如圖4所示。電壓環提供電感電流的給定,電流環采用誤差放大器對送入的電感電流給定(Vcv)和反饋信號(iLRs)之差進行比較、放大,得到的誤差放大器輸出Vc再和三角波Vs進行比較,最后即得控制占空比的開關信號。圖4中Rs為采樣電阻。對于一個設計良好的電流誤差放大器,Vc不會是一個直流量,當開關導通時,電感電流上升,會導致Vc下降;開關關斷,電感電流下降時,會導致Vc上升。電流環的設計原則是,不能使Vc上升斜率超過三角波的上升斜率,兩者斜率相等時就是最優。原因是:如果Vc上升斜率超過三角波的上升斜率,會導致Vc峰值超過Vs的峰值,在下個周波時Vc和Vs就可能不會相交,造成次諧波振蕩。
[page]
采用斜坡匹配的方法進行最優設計后,PWM控制器的增益會隨占空比D的變化而變,如圖5所示。
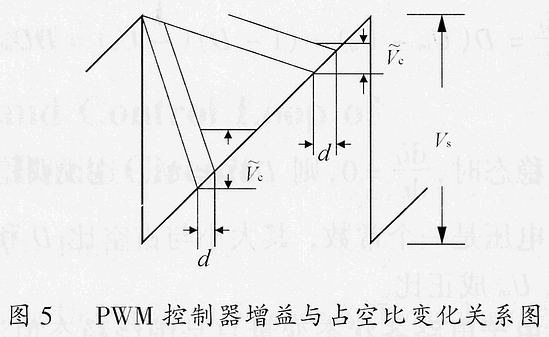
d=DV''''''''/Vs (17)
不妨設電壓環帶寬遠低于電流環,則在分析電流環時Vcv為常數。當Vc的上升斜率等于三角波斜率時,在開關頻率fs處,電流誤差放大器的增益GCA為
GCA[d(iLRs)/dt]=GCA(Vo/L)Rs=Vsfs (18)
GCA=Vc''''''''/(iL''''''''Rs)=VsfsL/(UoRs) (19)
高頻下,將式(14)分子中的“1”和分母中的低階項忽略,并化簡,得
iL''''''''(s)=[d(s)Uin]/sL (20)
由式(17)及式(20)有
(iL''''''''Rs)/Vc''''''''=[Rsd(s)Uin/(sL)]/[d(s)Vs/D]=(RsUinD)/(sLVs) (21)
將式(19)與式(21)相乘,得整個電流環的開環傳遞函數為
(RsUinD/sLVs)·(VsfsL)/(UoRs)=fs/s (22)
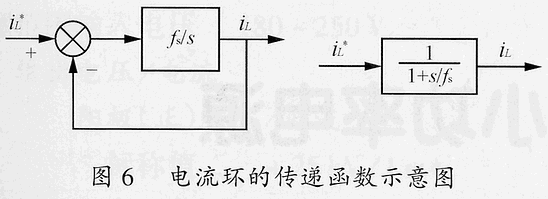
將s=2πfc代入上式,并令上式等于1時,可得環路的剪切頻率fc=fs/(2π)。因此,可將電流環等效為延時時間常數為一個開關周期的純慣性環節,如圖6所示。顯然,當電流誤差放大器的增益GCA小于最優值時,電流響應的延時將會更長。
GCA中一般要在fs處或更高頻處形成一個高頻極點,以使fs以后的電流環開環增益以-40dB/dec的斜率下降,這樣雖然使相角裕量稍變小,但可以消除電流反饋波形上的高頻毛刺的影響,提高電流環的抗干擾能力。低頻下一般要加一個零點,使電流環開環增益變大,減小穩態誤差。
整個環路的結構如圖7所示。其中KEA,KFB定義如前。可見相對VMC而言(參見圖3),平均CMC消除了原來由濾波電感引起的極點(新增極點fs很大,對電壓環影響很小),將環路校正成了一階系統,電壓環增益可以保持恒定,不隨輸入電壓Vin而變,外環設計變得更加容易。
4 峰值電流模式控制(PeakCMC)
平均CMC由于要采樣濾波電感的電流,有時顯得不太方便,因此,實踐中經常采用一種變通的電流模式控制方法,即峰值CMC,如圖8所示。電壓外環輸出控制量(Vc)和由電感電流上升沿形成的斜坡波形(Vs)通過電壓比較器進行比較后,直接得到開關管的關斷信號(開通信號由時鐘自動給出),因此,電壓環的輸出控制量是電感電流的峰值給定量,由電感電流峰值控制占空比。
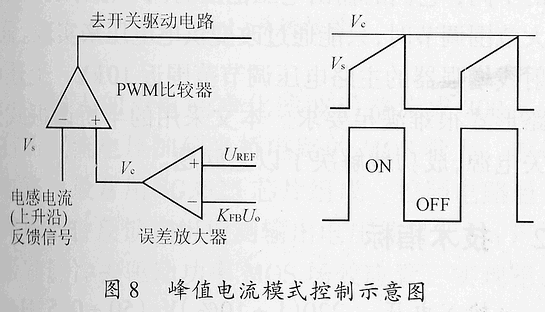
峰值CMC控制的是電感電流的峰值,而不是電感電流(經濾波后即負載電流),而峰值電流和平均電流之間存在誤差,因此,峰值CMC性能不如平均CMC。一般滿載時電感電流在導通期間的電流增量設計為額定電流的10%左右,因此,最好情況下峰值電感電流和平均值之間的誤差也有5%,負載越輕誤差越大,特別是進入不連續電流(DCM)工作區后誤差將超過100%,系統有時可能會出現振蕩現象。在剪切頻率fc以下,由圖6可知平均CMC的電流環開環增益可升到很高(可以>1000),電流可完全得到控制,但峰值CMC的電流環開環增益只能保持在10以內不變(峰值電流和平均值之間的誤差引起),因此,峰值CMC更適用于滿載場合。
峰值CMC的缺點還包括對噪音敏感,需要進行斜坡補償解決次諧波振蕩等問題。但由于峰值CMC存在逐周波限流等特有的優點,且容易通過脈沖電流互感器等簡單辦法復現電感電流峰值,因此,它在Buck電路中仍然得到了廣泛應用。
5 結語
采用平均狀態方程的方法可以得到Buck電路的小信號頻域模型,并可依此進行環路設計。電壓模式控制、平均電流模式控制和峰值電流模式控制方法均可用來進行環路設計,各有其優缺點,適用的范圍也不盡相同。







