圖1是單激式開關電源的基本原理圖。圖中,T為開關變壓器,N1和N2分別為開關變壓器初、次級線圈; 為開關變壓器的漏感,
為開關變壓器的漏感,![]() 為開關變壓器初級線圈的勵磁電感;
為開關變壓器初級線圈的勵磁電感;![]() 為開關變壓器初級線圈的分布電容,
為開關變壓器初級線圈的分布電容,![]() 為開關變壓器次級線圈的輸出負載,Q1為電源開關管。
為開關變壓器次級線圈的輸出負載,Q1為電源開關管。
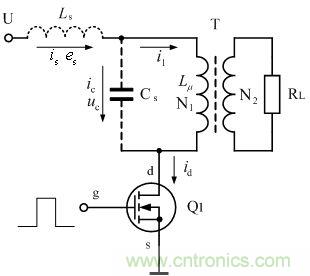
圖1 開關電源的基本電路
變壓器初級線圈或次級線圈的分布電容Cs可按下式進行計算:
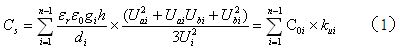
式中,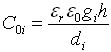 為第
為第![]() 層與+1層線圈之間的靜態電容,
層與+1層線圈之間的靜態電容,![]() = 1、2、3、• • •、n ,n為所求總分布電容的變壓器初級線圈或次級線圈的層數;
= 1、2、3、• • •、n ,n為所求總分布電容的變壓器初級線圈或次級線圈的層數;![]() 為第
為第![]() 層與
層與![]() +1層線圈之間的平均周長;
+1層線圈之間的平均周長;![]() 為第
為第![]() 層與
層與![]() +1層線圈之間分布電容的動態系數,
+1層線圈之間分布電容的動態系數,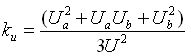 ,它與加到電容兩端的電壓有關,
,它與加到電容兩端的電壓有關,![]() 是一個小于1的系數;
是一個小于1的系數;
 為第
為第![]() 層與
層與![]() +1層線圈之間的標準電位差,其值一般等于相鄰兩層線圈工作電壓之和,即:
+1層線圈之間的標準電位差,其值一般等于相鄰兩層線圈工作電壓之和,即:![]() ,U為變壓器初級線圈或次級線圈兩端的工作電壓;
,U為變壓器初級線圈或次級線圈兩端的工作電壓;![]() 、
、![]() 分別為第
分別為第![]() 層與
層與![]() +1層線圈之間x=0和x=h處對應的電位差;當線圈層間按S繞法時,
+1層線圈之間x=0和x=h處對應的電位差;當線圈層間按S繞法時,![]() = 0,
= 0,![]() =
= ;當線圈層間按Z繞法時,
;當線圈層間按Z繞法時,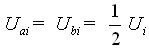 。
。
[member]
如果不考慮變壓器次級線圈對初級線圈的影響,對于一個功率大約為100瓦的開關變壓器,其初級線圈的分布電容大約在100~2000微微法之間;如果把次級線圈的分別電容也考慮進去,總的分布電容可能要大一倍左右,因為初、次級線圈分布電容的轉換比是平方的關系。因此,分布電容對輸出波形的影響是很大的。
根據變壓器的工作原理,圖1中的開關變壓器還可以等效為圖2所示電路。
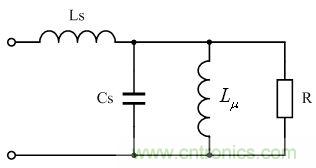
圖2 開關變壓器的等效電路
在圖2中,Ls為漏感,漏感也稱漏磁電感,或稱分布電感;Cs為分布電容(總分布電容), lu為勵磁電感,R為等效負載電阻。設開關變壓器初級線圈的電感為L,則g2 ;而分布電容Cs,則包括次級線圈等效到初級線圈一側的分布電容,即,次級線圈的分布電容也要等效到初級線圈回路中;同理,等效負載電阻R,就是次級線圈的負載RL被等效到初級線圈回路中的電阻。
設次級線圈的分布電容為C2,等效到初級線圈后的分布電容為C1,則有下面關系式:
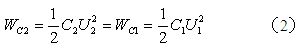
上式中,![]() 為次級線圈分布電容
為次級線圈分布電容![]() 存儲的能量,為
存儲的能量,為![]() 等效到初級線圈后的分布電容
等效到初級線圈后的分布電容![]() 存儲的能量;
存儲的能量;![]() 、
、![]() 分別為初、次級線圈的電壓,
分別為初、次級線圈的電壓,![]() 為變壓比,
為變壓比,![]() 、
、![]() 分別為初、次級線圈的匝數。由此可以求得
分別為初、次級線圈的匝數。由此可以求得![]() 為:
為:
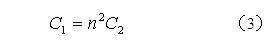
(2)和(3)式的計算方法不但可以用于對初、次級線圈分布電容等效電路的換算,同樣可以用于對初、次級線圈電路中其它電容等效電路的換算,以及用于對負載電阻的換算。所以,![]() 亦可以是次級線圈電路中的任意電容,
亦可以是次級線圈電路中的任意電容,![]() 為
為![]() 等效到初級線圈電路中的電容。
等效到初級線圈電路中的電容。
由此可以求得圖2中,變壓器的總分布電容Cs為:
![]()
(4)式中,Cs為變壓器的總分布電容,Cs1為變壓器初級線圈的分布電容;而C1為次級線圈電路中所有電容等效到初級線圈電路中的電容;C2為次級線圈電路中所有電容(包括分布電容與電路中的電容);n = N2/N1為變壓比。
雖然看起來,圖2開關變壓器的等效電路與一般變壓器的等效電路沒有根本的區別,但開關變壓器的等效電路一般是不能用穩態電路進行分析的;即:圖2中的等效負載電阻R不是一個固定參數,它會隨著開關電源的工作狀態不斷改變。例如,在反激式開關電源中,當開關管導通時,開關變壓器是沒有功率輸出的,即負載電阻R等于無限大;而對于正激式開關電源,當開關管導通時,開關變壓器是有功率輸出的,即負載電阻R既不等于無限大,也不等于0 。因此,分布電感與分布電容對正激式開關電源和反激式開關電源工作的影響是不一樣的。
圖3是開關變壓器與電源開關管連接時的工作原理圖。圖3中,Q1為開關管,Cds為開關管漏極和源極之間的分布電容,Cgs為開關管柵極和源極之間的分布電容。值得說明的是,這里的Cgs和Cds都不是一個單純性質的電容,它只是在開關管的導通和關斷的一瞬間,其阻抗的變化過程與電容(或電感)的充放電過程很類似;而它的基本性質實際上還是屬于電阻,因為它會損耗功率。
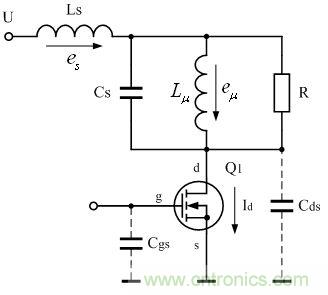
圖3 單激式開關電源等效電路
當開關管開始導通時,外電路給柵極(絕緣柵場效應管)加一正電壓,通過靜電感應,開關管耗盡層中的載流子(電子)在電場的作用下會重新進行分布,耗盡層中載流子濃度按指數規律不斷增加,這個過程相當于對電容Cgs進行充電;隨著耗盡層中載流子的重新分布,耗盡層的厚度也相應增加,其結果是耗盡層的電阻由大變小。
[page]
因此,當開關管剛開始導通時,流過開關管的電流是由小變大,這個過程,與在電感兩端加一電壓方波時,流過電感的電流由小變大很相似;所以,在開關管剛導通的一瞬間,開關管的漏極和源極之間可以等效成一個電感Lds。由于這個電感相對分布電感Ls和勵磁電感Lv來說很小,所以圖3中沒有畫出。
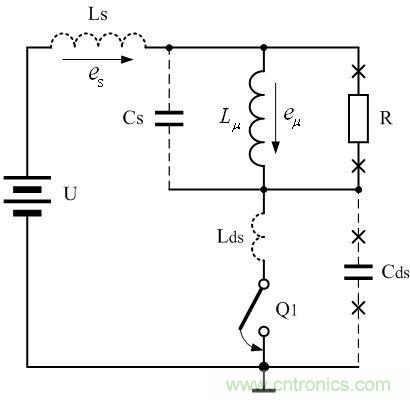
圖4 開關管導通時
圖4是圖3中的開關管Q1導通時對應的等效工作原理圖。在圖4中,電感Lds為開關管Q1導通時的等效電感,當開關管Q1導通時,開關管的內部電阻將隨時間由大逐步變小,它的作用好像一個電感,因此,當開關管Q1導通時,開關管可以等效成一個理想的開關與一個電感串聯。但這個電感屬于電阻性質,它會損耗能量,它不像實際中的電感那樣可以儲存能量(磁能),它實際上屬于一個阻值由大變小的可變電阻,但如果用一個可變電阻來表示,在計算過程中將會很復雜,并且在開關管Q1導通的變化過程中,用一個可變電阻來表示也沒有用一個電感來表示顯得形象。
當開關管開始關斷時,外電路給柵極加一負電壓(或低電壓),通過靜電感應,開關管內耗盡層中的載流子(電子)在電場的作用下會重新進行分布,相當于外電路要向耗盡層抽離載流子,耗盡層中載流子的濃度將按指數規律減小,耗盡層的厚度也將隨時間增大而變小,其結果是耗盡層的電阻將隨時間由小變大。這個過程,與電容被充電時,流過電容的電流由大變小很相似;所以,當開關管剛導通的一瞬間,開關管可以等效成一個理想的開關與一個電容器并聯,這個電容器就是漏極和源極之間的分布電容Cds。如圖5是開關管關斷時,反激式開關電源的工作原理圖。
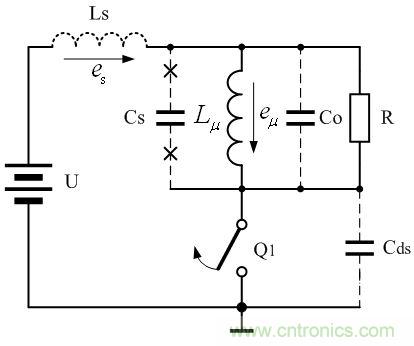
圖5 開關管關斷時
根據上面分析,柵極電容Cgs對開關管的導通影響比較大,容量越大,開關管的導通上升時間就越長。而漏極電容Cds對開關管的關斷影響比較大,容量越大,開關管關斷存儲時間就越長。電容Cgs和Cds也稱擴散電容,它們既具有電阻的性質,同時也具有電容充放電的特性,這種特性主要與耗盡層中載流子的濃度變化有關。
當電源開關管為晶體管時,Cgs和Cds分別與Cbe和Cce對應,工作原理場效應管的工作原理基本相同或相似。不過基區參與導電的載流子的密度的增加或減少,不是靠靜電感應的作用,而是靠基極電流的注入。
由于開關管在導通或關斷期間,其分布參數的性質和作用也在改變,因此,在圖1~5中,要對分布電感Ls和分布電容Cs,以及Cgs和Cds組成的電流回路進行精確計算,難度是很大的。下面,我們將以很長的篇幅來對上面電路進行分析和計算。
在圖4中,分布電感Ls和分布電容Cs可以看成是一個串聯振蕩回路,當開關管Q1開始導通的時候,輸入脈沖電壓的上升率遠遠大于輸入電壓通過分布電感Ls對分布電容Cs充電電壓的上升率,此時,串聯振蕩回路開始吸收能量,輸入電壓通過Lds和Ls對Cs進行充電,流過Ls和Cs的電流按正弦曲線增長;當開關管Q1完全導通以后,Lds的值等于0,此時,輸入脈沖進入平頂階段,相當于輸入脈沖電壓的上升率為0,由于,輸入脈沖電壓的上升率遠遠小于分布電感Ls與分布電容Cs進行充、放電時電壓的上升率,因此,振蕩回路開始釋放能量,振蕩回路會產生阻尼振蕩。
由于分布電感Ls和分布電容Cs的時間常數相對于勵磁電感比較小,所以分布電感Ls和分布電容Cs產生阻尼振蕩的過程主要發生在開關管Q1導通和關斷的一瞬間。當開關管Q1導通或關斷后不久,阻尼振蕩很快就會停止。當輸入電壓對分布電容Cs充滿電后,輸入電壓就完全加到勵磁電感的兩端。如果是反激式開關電源,流過勵磁電感的電流將隨時間從0開始線性增加;如果是正激式開關電源,流過勵磁電感的電流將隨時間按梯形波曲線增長。
在開關管Q1導通期間,由于開關管的導通內阻非常小,分布電容Cds基本上是不起作用的。當開關管Q1由導通狀態轉換為關斷時,開關管漏極和源極之間的分布電容Cds將被接入電路中,分布電感Ls和勵磁電感將同時產生反電動勢,并分別對分布電容Cds和Cs進行充、放電,電容與電感在交替進行能量交換的過程中,將產生串、并聯振蕩。
但由于勵磁電感的時間常數比Ls、Cs和Cds的時間常數大好多,因此,在產生振蕩的過程中,主要由Ls、Cs和Cds三者產生作用。另外,在開關管開始關斷期間,由于Cds實際上是一個阻抗由小到大,其阻抗變化過程類似于電容充電的可變電阻,它只吸收能量,而不會釋放能量。因此,它在產生振蕩的過程中,只對充電曲線的上升速率起影響,而對放電曲線的下降速率不起影響。
在下一講,陶老師將利用波形來具體分析開關管導通和關斷時,漏感及分布電容的工作過程,敬請期待......





