【導讀】電子產品設計日益輕薄,使得電源模塊亦須提升切換頻率以縮小體積。藉由傅里葉級數頻域分析,研發人員將可掌握切換式降壓轉換器電源模塊輸出端漣波變化量,從而搭配最適合的電感和電容,使電路板尺寸與能源效率達到最佳設計。
電子3C產品功能愈來愈豐富且IC制程的進化趨向于低壓大電流,使得芯片對電源的漣波及噪聲(Ripple Noise)要求更為嚴謹。數字產品強調輕薄,相對地,電源模塊為符合此要求勢必提升切換頻率以縮小外部零件體積。高頻漣波與噪聲對數字電路信號的影響勢必嚴重,尤其是影音(Video/Audio)信號及差動對數據傳輸信號(Differential Pair Signal)。
基于此因素,本文將以傅里葉函數(Fourier Series Expansion)方式來探討同步交換式降壓轉換器(Synchronous Step Down Converter)輸出電壓紋波的波形,并依電容完整等效串聯電阻(ESR)、等效串聯電感(ESL)、電容值(Capacitance)對應的公式,經由理論推導,有效地分析電源模塊輸出端紋波成分。
同步降壓交換式轉換器電路分析
同步降壓交換式電源轉換器的應用電路如圖1所示,系統工作原理是藉由交錯式切換High Side (Q1)/Low Side (Q2)金屬氧化物場效晶體管(MOSFET)(上、下橋晶體管),將輸入能量轉換成輸出端適當電壓以提供到負載側。系統關鍵性被動組件電感及輸出電容組成的低通濾波器(Low Pass Filter),用于傳送與儲存能量并濾除交流成分,讓輸出電壓成為平順的準直流需求。
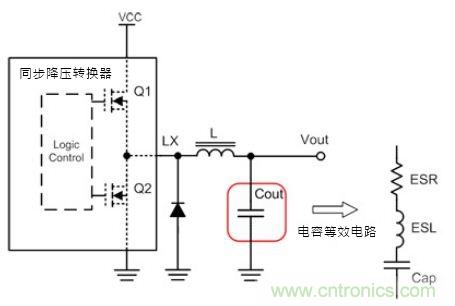
圖1 同步降壓轉換器應用電路
在常規技術的認知下,當切換頻率愈快,即可得到較小的輸出紋波,若以流經電感電流乘上輸出電容的等效串聯電阻來估算峰值紋波電壓是可得到近似數據,但與實際的輸出紋波波形有程度上的誤差,因此必須考慮電容完整的等效電路特性,便可獲得正確的解答。
在切換式降壓轉換器中,電感電流會對電容充電或放電,因此所有的紋波電流都會流經電容使得輸出到負載的電壓為穩定的直流電壓Vo。然而,實際情形不是如 此,因為實際電容除了本身電容值外,還包含等效串聯電阻與等效串聯電感參數特性,讓輸出紋波電壓(Ripple Voltage)ΔVo大于默認值,因此欲得到正確的輸出紋波,則須將如圖1所示完整的電容等效電路加以說明。
其中,Cap全稱為Capacitance,意思是電容值,其為電容最主要的參數,應用于電路穩壓,補償或濾噪聲之用,可用電容公式來表示其特性,亦即Q = C·Vc或
而ESR(Equivalent Series Resistance)為等效串聯電阻,其為電容能量損耗及紋波的來源,可用歐姆定律來表示其特性,亦即
至于ESL(Equivalent Series Inductance),表示等效串聯電感,可用電感微分公式來表示其特性,公式為
其感抗正比于頻率,在低頻時其感抗低,不易觀測到其作用,但在頻率較高時,其感抗增加,會降低電容穩壓濾波的功能。另外要補充的是,I為IL A.C成分,也就是電感電流的交流成分。
一般而言,在穩態(Steady State)及負載固定時,輸出電容的紋波電壓主要是由電感的紋波電流造成,可先計算出電感的紋波電流,再利用歐姆定律,電感微分公式及電容電荷儲存公式,分別計算出ESR、ESL及Capacitance的紋波電壓。再將此三種紋波加總起來,便可得輸出電容的紋波電壓,如公式1所示:
電感電流函數IL(t)可由公式2求得,其波形如圖2所示。在Ton時(上橋MOSFET導通),輸入電源VCC供應能量到負載端且電感組件儲存磁能(電感電流為線性遞增),依據法拉第定律(Faraday''s Law):
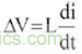
將可得到導通周期(On-time Duty)電感電流斜率:
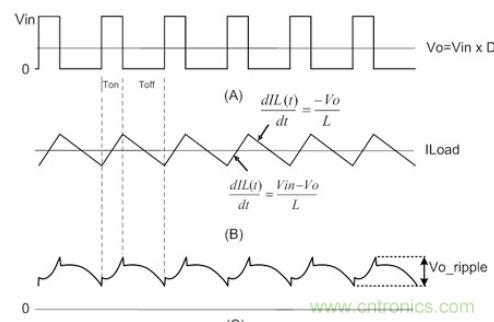
圖2 (A)LX的波形;(B)電感電流的波形;(C)輸出紋波波形
在Toff時(下橋MOSFET導通),電感釋放能量到負載(電感電流為線性遞減);其關斷周期(Off-time Duty)電感電流斜率如公式3所示:
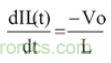 ......公式3
......公式3應用傅里葉函數頻域分析輸出紋波波形
依傅里葉級數展開任意周期性函數可得到頻率信號的幅度,也代表著信號在不同頻率分量成分的大小。頻域分析是以輸入信號的頻率為變量,并能夠提供比時域 (Time Domain)信號波形更直觀且包含頻率、振幅和相位信息。相對的傅里葉變換(Fourier Transform)可將頻域函數轉換成時域的穩態輸出紋波Vo。因此,傅里葉級數與傅里葉變換的優點是可讓分析者依所提供的任意輸入波形,容易得到輸出紋波波形。
周期T傅里葉級數為:
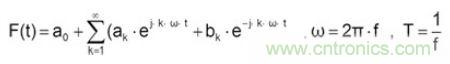
傅里葉系數則是:
等效電感阻抗包含ZESR、ZESL、ZCo,計算方式如下所示:
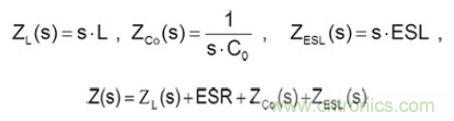
而LX電壓波形使用傅里葉級數展開,表示如下:
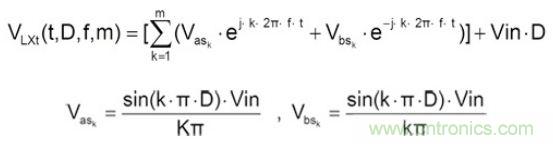
因此,ESR Ripple傅里葉級數展開如下所示:
ESL Ripple傅里葉級數展開如下所示:
Cap Ripple傅里葉級數展開如下所示:
Vo Ripple傅里葉級數展開如下所示:
應用傅里葉變換數值分析輸出電壓紋波
在處理信號時,常藉由傅里葉變換來取得信號所對應的頻譜,然后再由頻譜來讀取信號的參數。但由于所做的計算量過于龐大,當處理大量的數據時,則需要快速計 算的算法,因而衍生出快速傅里葉變換(Fast Fourier Transform, FFT)。快速傅里葉變換大幅提高了頻譜的計算速度。
快速傅里葉變換的使用條件包括:信號必須是周期性的、取樣周期必須為信號周期的整數倍、采樣率(Sampling Rate)必須高于信號最高頻率的兩倍以上、取樣點數N必須為2k個數據。
快速傅里葉變換原理的表示法,則如下所示:

舉例來說,當切換頻率(fsw)為1050kHz的降壓電路,輸入電壓為Vin=3.3伏特(V),Vo=1.8伏特,L=2.7微亨 (μH),Co=10微法(μF),ESR=4毫奧姆(mΩ),ESL=1.1奈亨(nH),fsw=280kHz。其實際量測的輸出電壓紋波、LX及電感紋波電流如圖3所示。若給予任意輸入波形,由傅里葉級數分析方法可得到對應的輸出紋波,利用此方法提供一個快速有效的方式,可分析計算輸入任意周期波的輸出紋波。
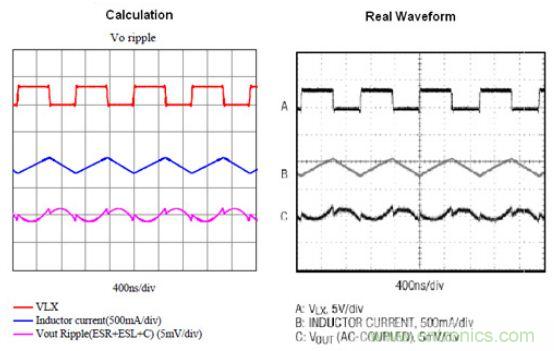
圖3 快速傅里葉變換模擬波形與實際量測波形
時域分析是以時間函數(Time Function)表示信號之特性,依據時間及振幅所組成之坐標平面來呈現出任何信號波形隨時間變化的瞬間物理量。時域分析輸出電壓紋波說明如下:
應用時域分析輸出紋波波形

選擇適當電感/電容值讓設計優化
本文提供了傅里葉級數頻域分析,其特色就是無須求解復雜的微分公式并與時域分析相對應,充分驗證理論推導及實際量測波形的對比。目的是想以較嚴謹的輸出電容等效電路來分析交換式降壓轉換器輸出紋波電壓。
經由上述論證可得知,電容的等效串聯電阻、等效串聯電感及電容值等特性均會影響輸出紋波振幅及相位,并利用基本的奧姆定律、電感的微分公式推導電感與電流紋波變化,及電容器依據操作頻率充/放電荷以維持輸出電位穩定。
將上述三種影響紋波因素波形(等效串聯電阻、等效串聯電感及電容值)線性迭加,便可得到完整的輸出紋波波形。透過此方法,可使研發工程師在設計切換式降壓轉換器電源時,根據電源需求及紋波允許變化量規格來選擇適當的電感和電容值,使其設計達到優化。
【推薦閱讀】
電池供電設備電流監控的三個要點——你真的做對了嗎?
詳解 LED PWM 調光技術及設計注意事項
電源小貼士:教你用分立組件設計穩健低成本的串聯線性穩壓器
汽車電源設計趨勢分析:從線性方案邁向開關方案
為可穿戴設備提供更出色的電源管理解決方案







