【導讀】在高性能電機和伺服驅動器中,基于隔離式sigma-delta(∑-?)的模數轉換器(ADC)已成為首選的相電流測量方法。這些轉換器以其強大的電流隔離和卓越的測量性能而聞名。隨著新一代ADC的推出,其性能也在不斷提高,但是,要充分利用最新的ADC的功能,就需要對其他的電機驅動器進行相應的設計。
本文介紹在電機控制應用中,使用sinc濾波器對∑-?編碼數據進行解調。然后,詳細探討了sinc濾波器和控制算法同步的不同方法。
電機驅動器制造商不斷提高其產品的性能和魯棒性。一些改進是通過采用更先進的控制算法和更高的計算能力實現的。其他改進則通過最小化反饋電路中的非理想效應來實現,比如延遲、傾斜和溫度漂移。
就電機控制算法的反饋而言,最關鍵的部分是相電流的測量。隨著控制性能提高,系統對時序精度、偏移/增益誤差、多反饋通道的同步等非理想效應越來越敏感。多年來,半導體公司一直致力于減少反饋信號鏈中的這些非理想效應,而且這種趨勢很可能會持續下去。ADuM7701就是為測量相電流而優化的最新一代隔離式∑-?ADC示例。雖然ADC的性能很重要,但也很可能在反饋路徑的其余部分造成非理想效應。本文不考慮ADC,主要討論反饋路徑的其余部分。雖然本文著重介紹電機控制應用,但它也適用于任何需要∑-?ADC緊密同步的其他系統。
ADuM7701
● 5 MHz 至 21 MHz 主時鐘輸入頻率
● 失調漂移與溫度:±0.6 μV/°C(最大值)
● SNR:86 dB(典型值)
● 16 位,無失碼
● 滿量程模擬輸入電壓范圍:±320 mV
● ENOB:14 位(典型值)
● IDD1:10 mA(最大值)
● 板載數字隔離器
● 工作溫度范圍:−40°C 至 +125°C
● 高共模瞬變抗擾度:150 kV/μs(最小值),VDD2= 3.3 V
● 寬體 SOIC
(1)16 引腳 SOIC_W
(2)8 引腳 SOIC_IC,爬電距離更長
使用∑-?ADC時的典型信號鏈如圖1所示。模擬輸入電壓通過讓相電流通過一個電阻分流器來產生。∑-?ADC將模擬信號轉換成1位數據流,并提供電氣隔離,因此ADC之后的一切都與電機相電位隔離。轉換器之后是通過濾波方式執行的解調。該濾波器將1位信號轉換為多位(M位)信號,并通過抽取過程降低數據更新速率。雖然濾波器抽取降低了數據速率,但速率通常仍然過高,無法匹配控制算法的更新速率。為了解決這個問題,我們增加了最后的降采樣階段。

圖1. 一種用于測量相電流的∑-?信號鏈。
本文假設濾波器和抽取級在FPGA中實現,并且濾波器是一個三階sinc濾波器(sinc3)
Sinc濾波器同步
∑-?ADC和sinc濾波器的缺陷在于很難在同一個時域中進行控制,并且缺少指定的采樣時刻。與具備專用的采樣保持電路的傳統ADC相比,這兩種濾波器都有一些令人擔憂的地方。不過也有辦法解決這個問題。如本節所示,將sinc濾波器與系統的其余部分同步,并在適當的時刻采樣相電流至關重要。如果未能正確做到這一點,測量結果將會大幅失真。
sinc濾波器的輸出并不代表該時刻∑-?ADC的輸入。相反,輸出是過去窗口期間輸入的加權平均值。這是由濾波器的脈沖響應造成的。圖2a顯示了抽取率為5時sinc3的脈沖響應。從圖中可以看出,濾波器輸出如何成為輸入序列的加權和,中間的采樣獲得較大權重,而序列開始/結束時的采樣權重較低。
在繼續討論之前,需要給出幾個基本定義。∑-?ADC時鐘,又稱為調制器時鐘,表示為 fmod。抽取率(DR)決定抽取頻率(fdec),并與fmod關聯,如公式1所示:
圖2右側顯示了脈沖響應對濾波器階躍響應的影響。應用該步驟時,濾波器輸出不受影響,濾波器在3個完整的抽取周期之后達到穩定狀態。因此,sinc3濾波器的一些重要特性可以表述為:
● 群延遲為1.5個抽取周期
● 建立時間為3個抽取周期
在將濾波器與控制系統同步時,這些屬性非常重要,本文將始終會用到。
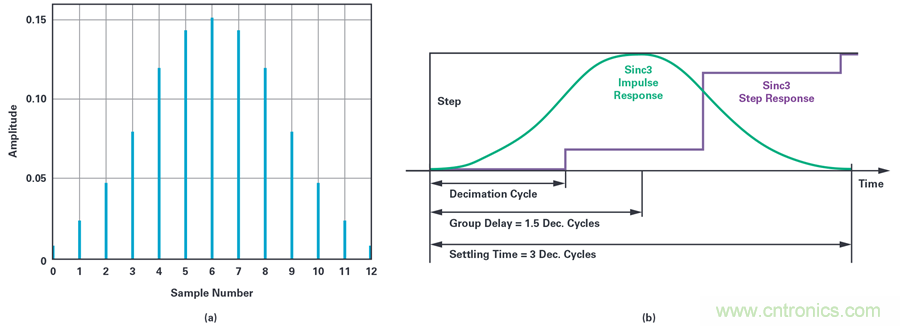
圖2.(a)濾波器抽取率為5的sinc濾波器脈沖響應。(b)Sinc濾波器的階躍響應以及與脈沖響應的關系。
在討論sinc濾波器同步之前,必須先定義輸入信號的特性。這反過來又會定義濾波器的同步特性。
圖3顯示了由電壓源逆變器驅動的3相永磁電機的模擬相電流。調制方式為空間矢量PWM,開關頻率為10kHz。將電機加載到5A峰值相電流和3000rpm轉速。這種設置加上3個極對數,可以得到6.67ms電氣基本周期。
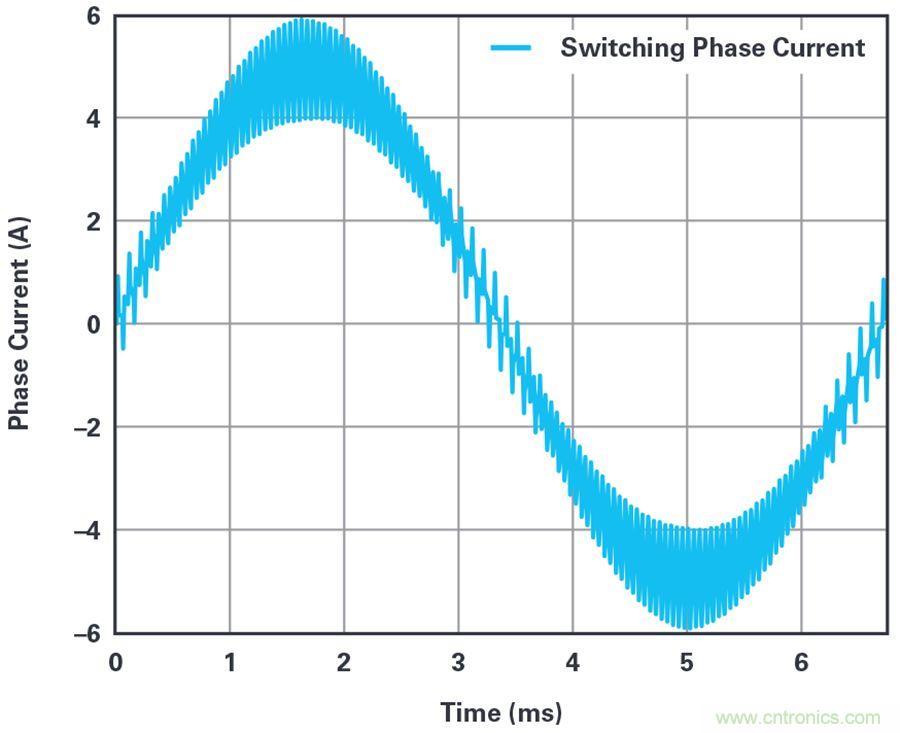
圖3. 采用空間矢量脈寬調制時的電機相電流。
相電流可以看作由兩個分量組成:平均分量和開關分量。出于控制目的,僅關注電流的平均分量,因此必須完全去除開關分量。要提取平均分量,最常見的方法是對與PWM同步的信號(用于電機終端)進行采樣。如圖4所示。最上面的信號顯示相電流的開關波形,中間的信號顯示對應的逆變器相位臂的高端PWM,最下面的信號顯示來自PWM定時器的同步信號。PWM同步信號在PWM周期的開始和中間進行置位。為簡明起見,假設所有三相的占空比都是50%,意味著電流只有一個上升斜坡和一個下降斜坡。在PWM同步信號的上升沿,電流取其平均值,因此如果恰好在那一刻采樣電流,開關分量將被完全抑制。實際上,采樣保持電路相當于一個在開關頻率上具有無限衰減的濾波器。
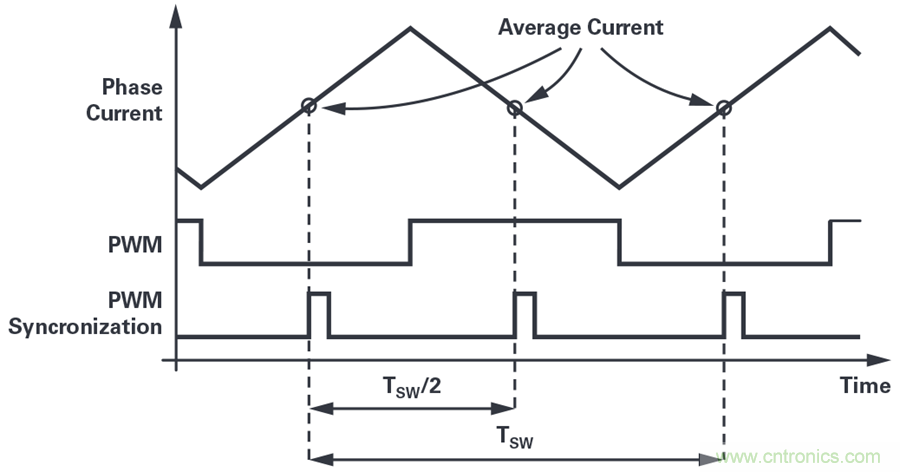
圖4. 在PWM周期的起始點和中心點處測量相電流會減弱電流紋波。
圖5顯示了將這種采樣應用于圖3中所示波形時的結果。右側所示是實際相電流和采樣電流的波形放大圖。注意采樣保持過程如何完全消除紋波。
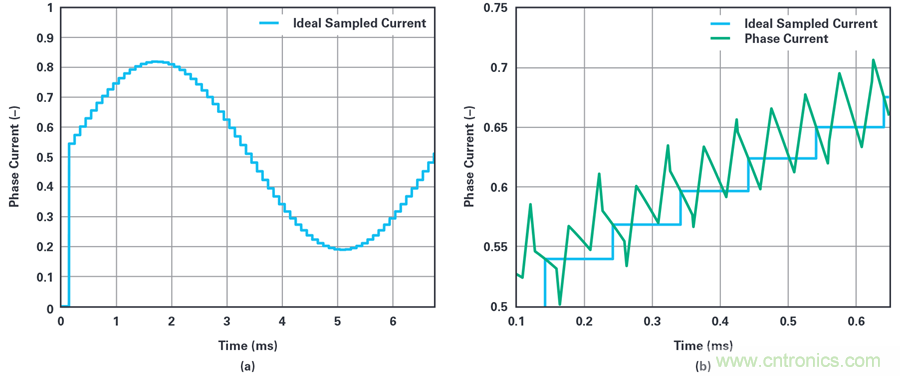
圖5.理想的相電流采樣:(a)理想的采樣相電流的基波周期,(b)相電流和采樣相電流的波形放大圖。
采樣電流以每單位表示,其中0A映射到0.5,全比例值為8A。選擇這個比例是為了更容易與后面的∑-?測量值進行比較。圖5所示的結果為理想場景,采樣后只剩下基波分量。因此,可以將這些數據當做比較∑-?測量值的基準值。
∑-?測量和混疊
在理想的采樣保持ADC中,由于嚴格控制采樣時刻,所以能夠提取基波分量。然而,∑-?轉換是一個連續的采樣過程,紋波分量將不可避免地成為測量的一部分。
在∑-?轉換中,抽取率與信噪比(SNR)之間存在密切聯系。抽取率越高,輸出的有效位數(ENOB)越多。缺點是,隨著抽取率增加,群延遲也會增加,因此設計者必須在信號分辨率和反饋鏈的延遲之間折中考量。一般來說,與控制周期相比,應將延遲保持在較小范圍。對于電機控制,典型的抽取率在128到256之間,這可以很好地平衡信噪比和群延遲。
在數據手冊規范中,通常使用256作為抽取率。例如,ADuM7701的ENOB為14位,抽取率為256。ENOB值如此高時,預計可以得到非常準確的測量結果。為了驗證這一點,假設圖3所示的相電流是采用∑-?ADC在20MHz時測量所得,數據流則由使用256抽取率的sinc3進行解調。結果如圖6a所示。
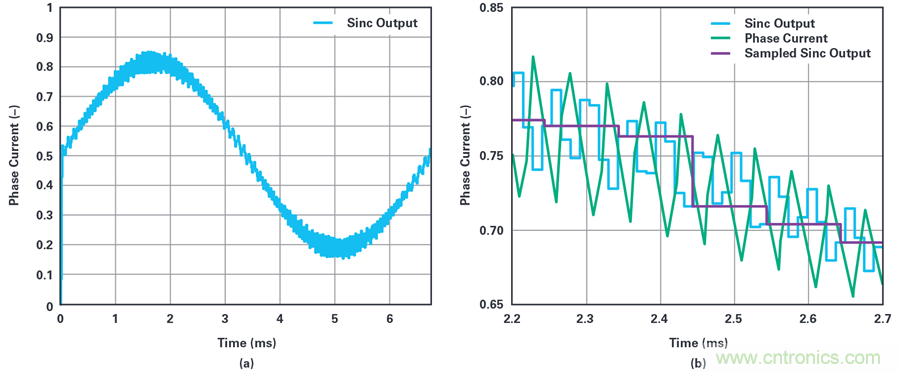
圖6. (a)sinc濾波器的輸出。(B)實際的相電流和sinc濾波器抽取輸出的波形放大圖。
相電流的基波分量非常明顯,但與圖5a所示的理想采樣相比,測量信號存在很大的噪聲。因此,雖然ADC和sinc濾波器本身提供了不錯的ENOB數量,但反饋信號的質量卻很差。從圖6b可以看出其原因,該圖是sinc濾波器輸出和實際的相電流的波形放大圖。注意相電流的10kHz開關分量是如何發生相移,以及幾乎未被sinc濾波器衰減。現在,假設在每個PWM周期執行一次電機控制算法,并在周期開始時讀取最新的sinc濾波器輸出。實際上,sinc濾波器的輸出會向下采樣,以匹配控制算法的更新速率。向下采樣和得到的信號在圖6b中顯示為采樣sinc輸出。圖7a顯示了按照PWM速率濾波和采樣的整個基波周期的結果。
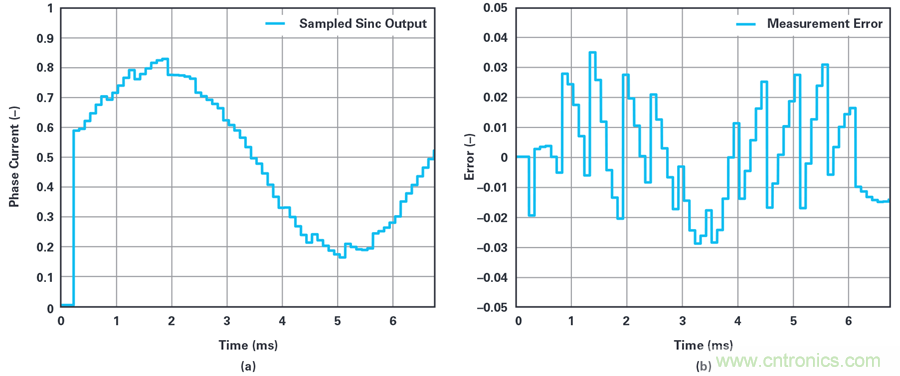
圖7. (a)sinc濾波器的采樣輸出。(b)測量誤差。
很明顯,相電流測量失真嚴重,因此控制性能會非常差。如此,應該增加扭矩波紋,并且需要降低電流控制環路的帶寬。從理想測量值(圖5a)中減去圖7a中的測量值,就可以得到誤差(圖7b)。誤差約為原比例信號的7%,與預期的14ENOB相差甚遠。
這個∑-?測量和混疊場景演示了基于∑-?的非常常見的電流測量模式,以及它是如何引導設計人員得出“∑-?ADC不適合電機驅動器”這個結論的。但是,這個示例并沒有顯示出ADC本身的糟糕性能。相反,因為未能正確設置相電流測量值,所以余下信號鏈的性能欠佳。
ADC在幾兆赫(一般為10MHz至20Hz)下對輸入信號采樣,在抽取率為256時,sinc濾波器有效去除調制噪聲。在如此高的采樣率下,濾波器輸出中存在相電流紋波分量,在信號鏈的向下采樣級,這可能成為一個問題(見圖1)。如果紋波分量沒有充分衰減,且電機控制算法以PWM速度消耗電流反饋,則結果會因為降采樣而產生混疊。
根據標準采樣理論,為了避免混疊,信號在一半采樣頻率以上時必須無能量。如果對∑-?ADC輸出向下采樣至10kHz,那么5kHz或更高頻率下的噪聲將會混疊到測量值中。如圖所示,在sinc濾波器之后,信號中還存在大量10kHz開關噪聲。降低10kHz噪聲的一種方法是增加抽取率,但是這樣做會導致不可接受的長時間群延遲。我們需要采用一種不同的方法。
通過同步改善測量
上一節討論的抗混疊方法的主要問題如圖8所示。sinc濾波器的輸出在與相電流開關分量無關的某個時刻被讀取。輸出信號被讀取時,濾波器根據脈沖響應對輸入信號進行加權平均。這個加權平均值有時跨越開關波形的低點,有時跨越高點。因此,用作反饋的信號含有明顯噪聲,頻率從0Hz到PWM頻率的一半。
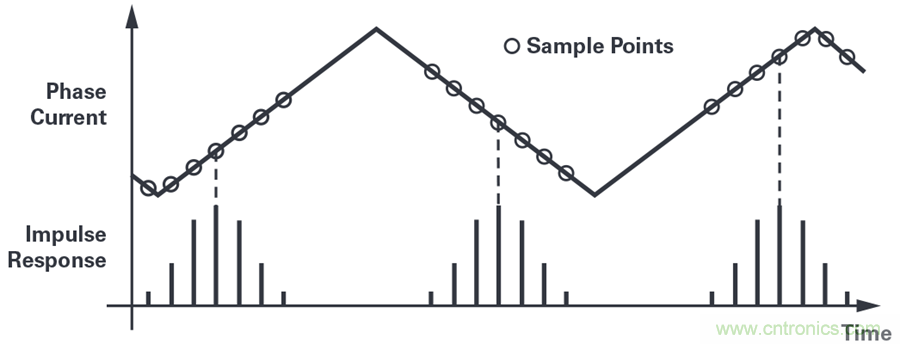
圖8. 脈沖響應與開關波形無關。
∑-?ADC連續采樣,sinc濾波器輸出乘以每個PWM周期的測量值(通常10到20)。由于每次測量跨越3個抽取周期,所以脈沖響應會重疊。為了簡化起見,圖8中僅顯示三個測量/脈沖響應。
問題的根源在于:脈沖響應沒有鎖定為電流的開關分量,而開關分量又被鎖定為PWM。解決方案是選擇抽取率,使每個PWM周期都有固定的整數抽取周期。例如,如果PWM頻率為10kHz,調制器時鐘為20MHz,抽取率為200,那么每個PWM周期正好有10個抽取周期。每個PWM周期有固定的采樣周期,脈沖響應始 終鎖定為PWM,用于反饋的測量值在PWM周期內的同一點被捕獲。采用這種同步方案的相電流測量如圖9a所示。
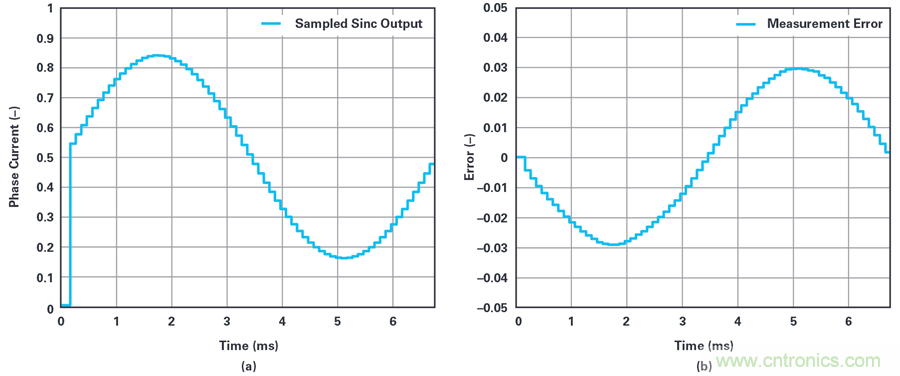
圖9.(a)脈沖響應鎖定采用PWM時,sinc濾波器的采樣輸出。(b)測量誤差。
顯然,將響應同步與PWM同步會產生積極的影響。噪聲會被消除,且乍一看,測量結果似乎與圖5a中的理想測量值相似。但是,用理想測量值減去∑-?測量值時,就會得出圖9b所示的誤差信號。誤差大小與圖7b中所示的值相似,但頻譜發生了變化。現在,誤差是一階諧波,相當于增益誤差。導致這種錯誤模式的原因如圖10所示。
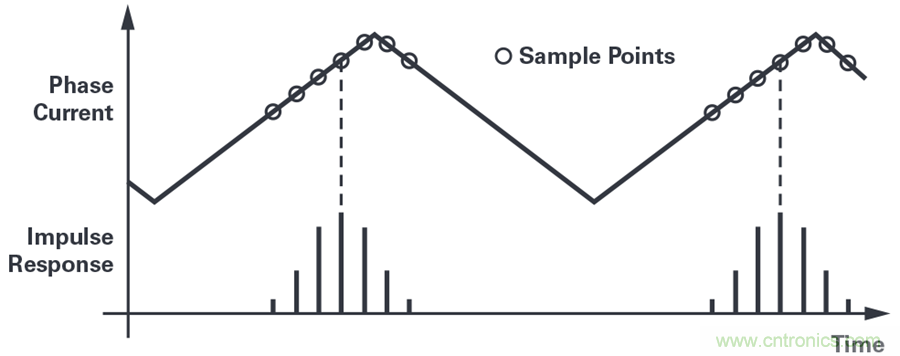
圖10. 脈沖響應被鎖定為開關周期內的某個固定點。
雖然消除了白噪聲誤差分量,但由于測量值受到開關分量的影響,信號仍然是失真的。在圖10中,注意sinc濾波器的脈沖響應如何圍繞開關波形的峰值給出加權平均值。根據脈沖響應相對于PWM的相位,偏差的大小僅受紋波電流的大小限制。如圖3所示,紋波分量的幅值在基波周期內發生變化,基波電流峰值時紋波最高,過零點時紋波最低。因此,測量誤差為一階諧波分量。
為了消除一階諧波測量誤差,脈沖響應必須始終以PWM周期的起始點或中心為中心,此時相電流正好等于其平均值。圖11顯示了以開關周期的起始點為中心的脈沖響應。在這一點周圍,開關波形是對稱的,因此,通過在每一邊都有相同數量的測量點,紋波分量在這一點周圍均為零。
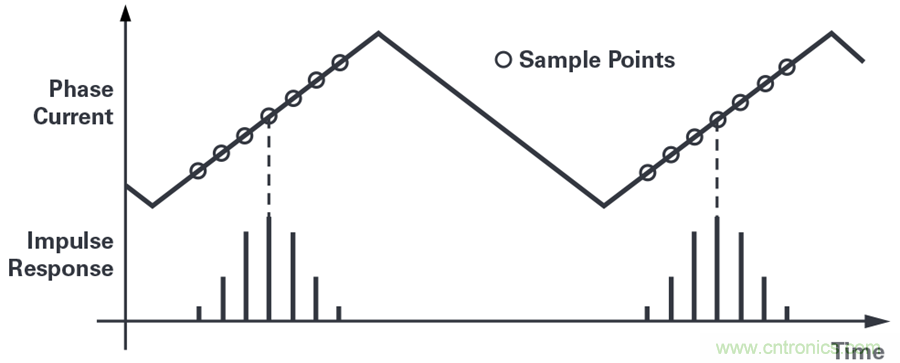
圖11. 脈沖響應鎖定為開關周期,并對準理想的測量點。
脈沖響應鎖定,以平均電流的時刻為中心時,測量結果如圖12a所示,測量誤差如圖12b所示。作為理想的采樣測量,該信號不存在白噪聲和增益誤差。
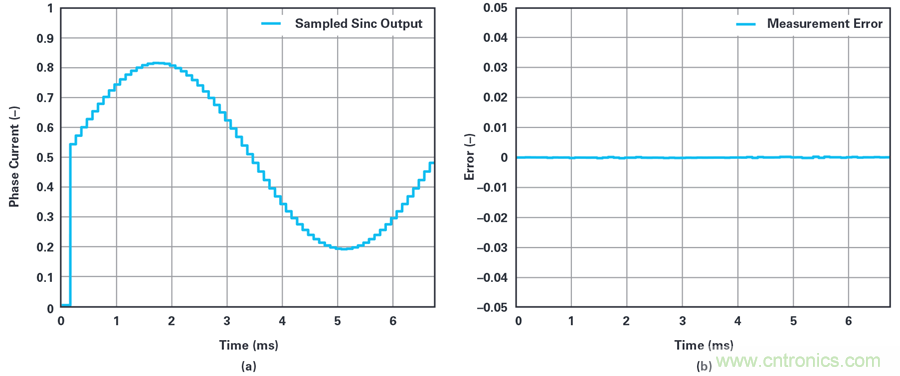
圖12. (a)脈沖響應鎖定采用PWM,且以平均電流時刻為中心時,sinc濾波器的采樣輸出。(b)測量誤差。
結果表明,∑-?測量值的質量不僅僅取決于抽取率。只有在無混疊時,普遍認為“增加抽取率會提高ENOB”的這種觀點才是正確的。控制濾波器相對于輸入信號的更新率和相位比抽取率更重要。例如,比較圖7(基于256的抽取率)和圖12(基于200的抽取率)。降低抽取率可顯著改善測量結果。
結論
綜上所述,實現基于∑-?的優化相電流測量值的條件如下:
● 三階sinc濾波器的脈沖響應時間為3個抽取周期,這意味著數據需要3個抽取周期才能通過濾波器。
● 濾波器的脈沖響應必須以平均電流時刻為中心。
● 脈沖響應的1.5個采樣周期必須在平均電流時刻之前,另外1.5個采樣周期必須在平均電流時刻之后。
● sinc濾波器在PWM周期內產生多個輸出,但只使用其中一個輸出。其余的輸出都被忽略。
推薦閱讀:








