【導讀】當我們在聽一首歌時,我們把正弦波形看作音樂。它們的振幅告訴我們信號有多大,頻率告訴我們聲音是低音還是高音。然而,第三個重要參數,即相位,我們的耳朵是感覺不到的。本文將解釋并給出更多關于相位參數的細節,因此,第一節將介紹相位和相位差的概念。在第二部分,我們詳細介紹了相移概念的更多方面,并著重討論了當信號不存在時的特定情況同步化了第三節和最后一節將最后介紹相位差在干涉現象中的重要作用。
演示
正弦信號的相位通常用Φ表示,并以弧度(rad)或度數(°)測量,可以在-π和+πrad或-180°和+180°之間變化。在圖表中,交流信號的相位表示其相關正弦函數在時間原點的初始狀態:
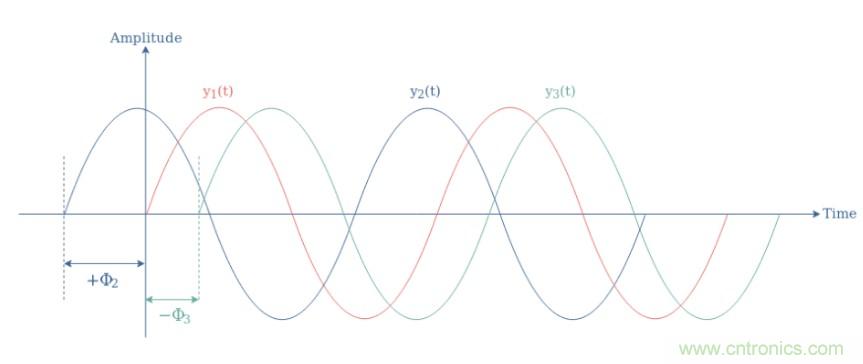
圖1:具有不同相位的三個正弦波的圖示
一個信號的相位Φ可以有三種不同的性質,它決定了波形繞縱軸的位置:
等于0(°或rad),例如用作參考信號的信號y1(t)
如信號y2(t)為正
如信號y3(t)為負
單個信號的相位不是很相關,因為無論交流波形是電的還是機械的,如果信號有相位,感知將保持不變。更重要的是,可以清楚地感知到的是相位差,也稱為相同頻率的兩個信號之間的相移。
相位差
在相同頻率的信號之間重要的是在這一節中我們只討論兩個頻率相同的信號之間的相移。因此,考慮具有不同相位和可能不同振幅的兩個相同頻率的信號:y1(t)=Asin(ωt+Φ1)和y2(t)=Bsin(ωt+Φ2)。我們將相位差定義為ΔΦ21=Φ2-Φ1。在圖1中,我們有ΔΦ21=+Φ2,ΔΦ31=-Φ3,以及ΔΦ32=-Φ3-Φ2。正相位差,如ΔΦ21,表明信號y2(t)暫時先于參考信號y1(t),我們也認為y2(t)超前于y1(t)。負相位差,如ΔΦ31和ΔΦ32,表明信號y3(t)跟隨信號y1(t)和y2(t),我們也說y3(t)滯后于y1(t)和y2(t)。在相位差可以取的-180°和+180°或-π和+πrad之間的所有值中,可以突出顯示幾個,如下圖2所示:
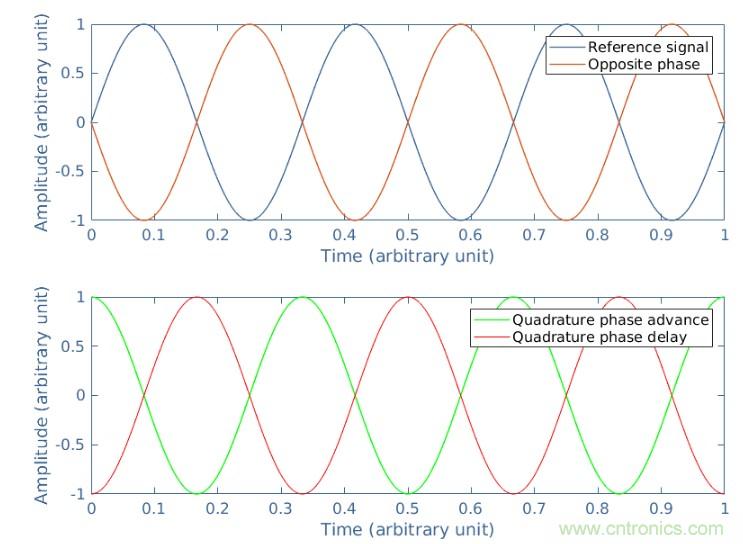
圖2:一些相關相移的圖示
相反相的特征是相移為+180°或+πrad,這與-180°或-πrad完全相同。如果參考信號為Vref=vrefsin(ωt),則相反的信號為Vopp=vrefsin(ωt+π)=-vrefsin(ωt),因此,Vref+Vopp=0。正交信號的特征是“前進”的相移為+90°或+π/2 rad,對于“延遲”,相移為-90°或-π/2 rad,我們特別關注電流(I)和電壓(V)信號在電偶極子上的相移,并研究其影響電源。輸入直流區,偶極子的耗散功率(P)由電壓和電流的乘積給出:
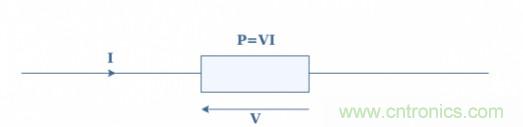
在交流系統中,這種表示不再是真實的,因為電壓和電流都是交替的。考慮偶極子的電壓為V=Vrms√2.sin(ωt),相同頻率的電流呈現+ΔΦ:I=Irms√2.sin(ωt+Φ)。以Vrms和Irms為均方根值。它可以證明,交流區偶極子中耗散的有功功率由公式1給出:
公式1:交流狀態下的耗散功率
cos(Φ)這個術語被稱為功率因數,它給出了受體吸收電源功率的效率。這個因子是一個介于0和1之間的實數,這兩個極值反映了截然不同的行為:如果cos(Φ)=1,偶極子被認為是純電阻,電壓和電流之間的相移為零。偶極子不存在任何感應或電容行為。如果cos(Φ)=0偶極子是純無功的,電壓和電流之間的相移最大,等于±90°或±π/2 rad。在這種情況下,偶極子不消耗任何功率,而是將其返回給電路。The方程式1中給出的功率稱為有功功率(P),Vrms×Irms的乘積稱為視在功率,并記下S。如果元件為純電阻元件,則為消耗的功率。Vrms×Irms×sin(Φ)是無功功率,并注明Q。由于在同一復雜功率圖中相移ΔΦ,這些量可以聯系起來:
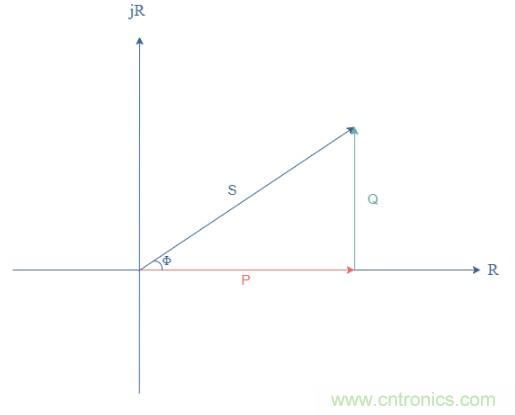
圖3:有功、視在和無功功率的定義
在本節中,我們考慮兩個頻率相近但不完全相同的信號y1(t)和Φ的相移y2(t):ω1≠ω2。通常,只能為兩個頻率相同的信號定義相移,但在這種特殊情況下,由于頻率相似,定義相位差仍然有意義。如果頻率相差太大,通常當ω1>2ω2時,由于相位差和信號一樣變化,因此定義它是沒有意義的本身。在在信號頻率相似的情況下,相位差不再是常數,而是隨時間緩慢變化:ΔΦ(t)=(ω2-ω1)t+Φ。這兩個信號的疊加很有趣,因為會產生拍頻現象,如圖4所示:
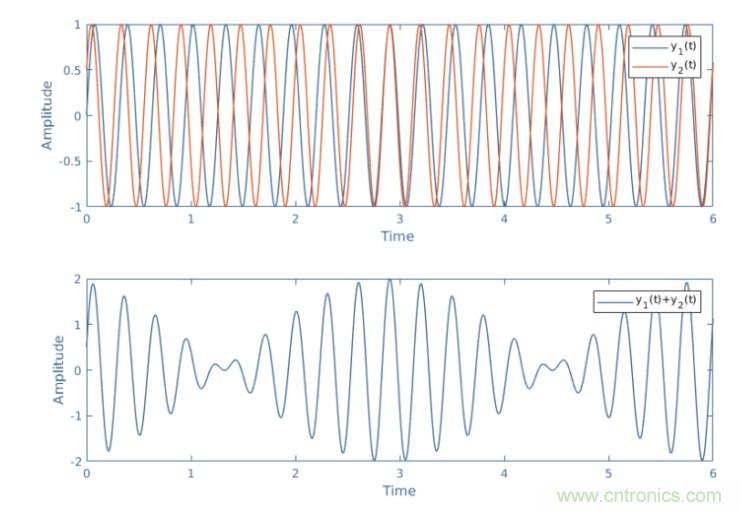
圖4:兩個頻率相近信號之間跳動現象的圖示
干擾
我們可以在圖4中看到,正弦波形的疊加有時除了信號處于相位時的振幅之外,有時會導致相距,或者當信號與相位相反時進行減法。這種現象被稱為干擾,當信號相同時發生頻率??紤]同樣頻率的正弦波形又有兩種:y1(t)=A1sin(ωt+Φ1)和y2(t)=A2sin(ωt+Φ2)。我們把y3(t)稱為疊加y1(t)+y2(t)和A3的振幅??梢钥闯?,y3(t)的振幅滿足以下公式:
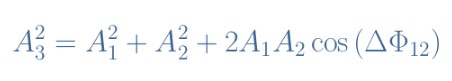
公式2:疊加信號的振幅
我們可以注意到y1(t)和y2(t)之間的相位差對最終的信號幅度起著重要的作用。有兩種情況值得注意:ΔΦ12=0,信號同相,振幅A3最大,滿足A32=(A1+A2)2。在這種情況下,我們認為y1和y2之間的干擾是建設性的,ΔΦ12=±πrad,信號相位相反,振幅A3最小,滿足A32=(A1-A2)2。在這種情況下,y1和y2之間的干擾是破壞性的。什么時候相位差在這兩個極值之間,我們可以繪制一個圖表,顯示A3隨ΔΦ12的變化:
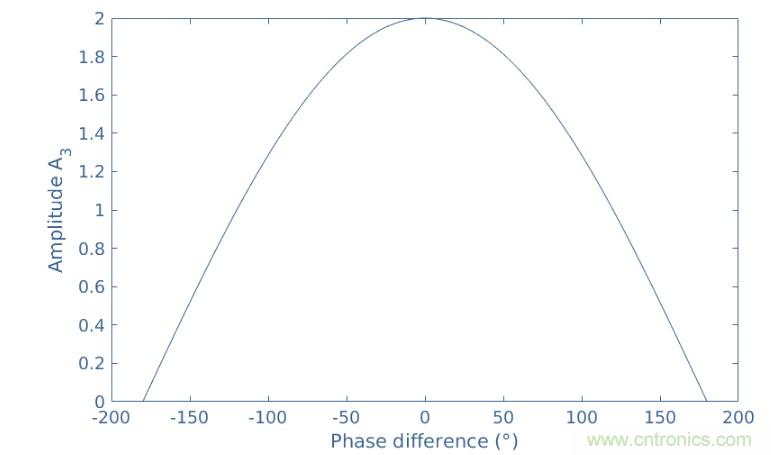
圖5:作為相位差函數的結果信號的振幅
在這個圖中,為了簡單起見,我們選擇A1=A2。我們又可以看到,當ΔΦ12=0,A3=A1+A2=2,當ΔΦ12=±180°時,A3=A1-A2=0。
結論
本教程詳細介紹了相位和相位差的概念,并通過一些例子指出了相位和相位差的重要性示例。首先總之,我們給出了什么是信號的相位,以及用什么單位來測量。然而,僅僅是相位的概念并不十分相關,在第二節的第一段中,我們定義了相移ΔΦ,并給出了一些與相位差的特殊情況相關的詞匯:同相(ΔΦ=0°),相位的對立(ΔΦ=±180°)和正交(ΔΦ=±90°)。在第二小節中,我們強調了電路中電流和電壓之間相移的重要性。在任何電子元件中消耗的功率與相移的余弦成正比,稱為功率系數。最后一節,我們將干涉現象與相移參數聯系起來并加以解釋。
推薦閱讀:







