【導讀】很多工程師朋友都在問關于PCB設計中一些反射的問題,大家問的很多都是基礎理論上,但是對一些知識點不是很明白,就差一層窗戶紙沒有捅破。這里一位技術牛人就這些問題分享了自己關于PCB設計中關于反射的理解和經驗,幫助大家捅破這層窗戶紙。
寫在前面的話:
接下來小編還會繼續為大家奉獻上該專家基于PCB設計中關于反射的其他相關知識,有的還會結合實例,可能會需要時間整理,希望大家耐心等待!
自出道以來,接到了大量朋友的提問,很大一部分問題幾種在基礎理論上。很明顯大家都是有思考過的,對一些東西處于明白但又有點不明白的區間,還差一層窗戶紙沒有捅破。所以寫出這樣一篇文章,希望能幫助大家捅破這層窗戶紙。
接下來小編還會繼續為大家奉獻上該專家基于PCB設計中關于反射的其他相關知識,有的還會結合實例,可能會需要時間整理,希望大家耐心等待!
自出道以來,接到了大量朋友的提問,很大一部分問題幾種在基礎理論上。很明顯大家都是有思考過的,對一些東西處于明白但又有點不明白的區間,還差一層窗戶紙沒有捅破。所以寫出這樣一篇文章,希望能幫助大家捅破這層窗戶紙。
基礎理論篇幅較長,所以這一系列文章會分比較多期。
前言
在國外能碰到許多二三十年工作經驗的工程師,幫助他們溝通的工具不是PPT,不是仿真結果,不是測試結果,而是一張紙和一支筆。
很佩服他們可以用一張紙一支筆給你勾繪出一個電路,一條波形,一種debug的方案。曾有一個老工程師告訴我,當你用場的角度去理解電路上的器件的時候,一切將會變得簡單起來。
什么叫場的角度理解分立器件?在這個世界里,容抗是Xc=1/(2πfC) ,感抗是XL= 2πfL=ωL 。
這兩個公式中的f與ω指的不是我們的信號頻率,而是正弦波的頻率與角頻率。
在這里,我們要感謝偉大的讓•巴普蒂斯•約瑟夫•傅立葉——簡稱傅立葉,對,就是發明傅立葉變化的那個人。
所以在大家眼中看到的信號是這樣的:
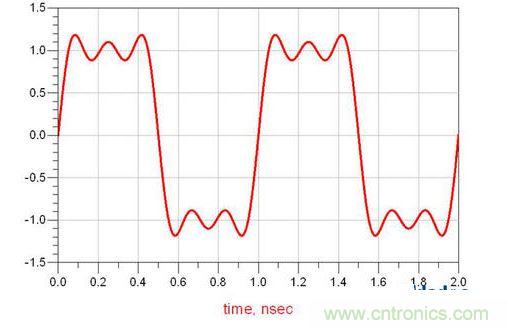
而在一個SI工程師的眼中看到的信號是這樣的:
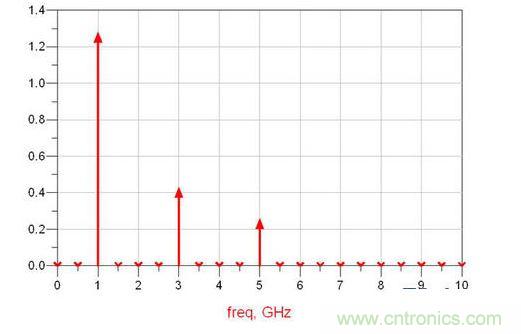
或者,這樣的:
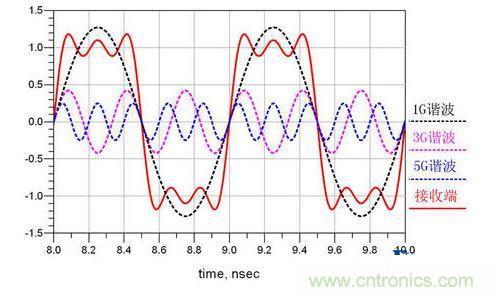
當我們能將信號分解為一個一個正弦波來研究的時候,一切都變簡單了,可以量化了。在正弦波的世界中只有頻率f,幅度A,相位θ。
現在,我們可以愉快的用場來看這個世界了。
[page]
讓我們來思考下面這個問題:
一個1V的正弦波在某岔路口分成了兩個大小相等的正弦波,兩條路通向同一個終點,但是一條路長為L,另外一條路長度為L+X,在終點的時候,這個正弦波變成了什么?
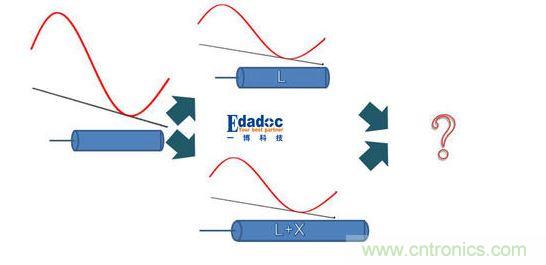
當兩條岔路一樣長時:
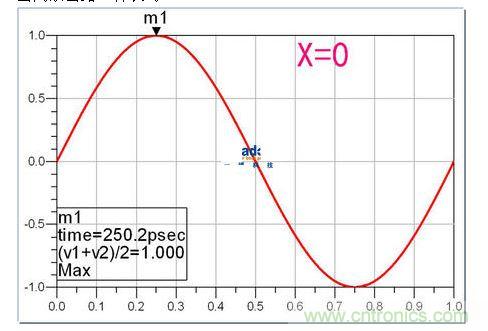
終點的信號和起點的信號沒有區別。
當一條路比另一條多二十分之一波長時:
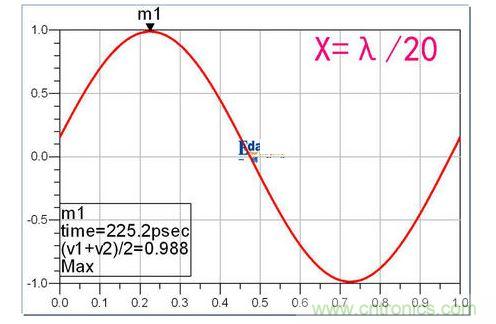
區別也十分小吧?高速先生在這里特別打上了mark點。大家可以看到,終點的信號比起點的信號衰減了1.2%。
[page]
X更長,達到八分之一波長時:
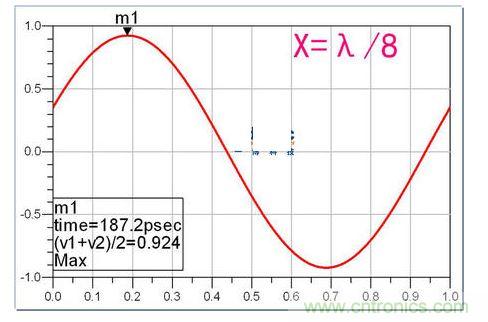
這時候,衰減已經不需要打mark點也可以看出來了。
X再長一點,達到四分之一波長時:
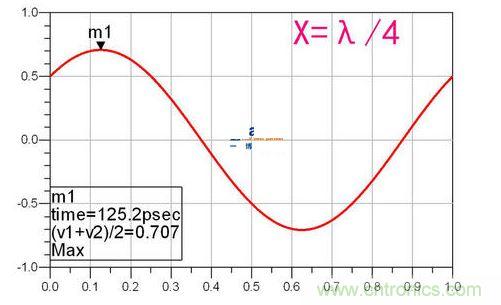
30%的能量不見了!
直到,X達到波長一半的長度:
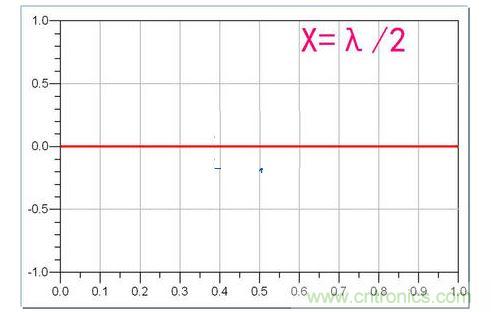
好慘,完全陣亡。
接下來小編還會繼續為大家奉獻上該專家基于PCB設計中關于反射的其他相關知識,有的還會結合實例,可能會需要時間整理,希望大家耐心等待!
接下來小編還會繼續為大家奉獻上該專家基于PCB設計中關于反射的其他相關知識,有的還會結合實例,可能會需要時間整理,希望大家耐心等待!







