【導讀】真實的生活如流水般不可中斷,而視頻攝像頭每秒鐘只記錄了有限數量的畫面。每一幀畫面可以捕捉到處于不同位置的車輪,而這也取決于在幀與幀之間車輪旋轉的圈數,它們也許真的看上去是向后旋轉的!這個效果被稱為混疊。
你看沒看到過汽車向前行駛,而車的輪子實際上是向后轉呢?如果不是在表演高難度特技的話,我打賭你一定在汽車廣告中看到過。你想沒想過這是為什么呢?
真實的生活如流水般不可中斷,而視頻攝像頭每秒鐘只記錄了有限數量的畫面。每一幀畫面可以捕捉到處于不同位置的車輪,而這也取決于在幀與幀之間車輪旋轉的圈數,它們也許真的看上去是向后旋轉的!這個效果被稱為混疊。
使用模數轉換器 (ADC) 的數據采集系統會經歷同樣的現象,原因在于這些系統對一個連續的時間信號進行了不連續的“抓拍”。在這篇博文中,我將簡要介紹ADC應用領域中的混疊到底是什么樣子的。

圖1:汽車廣告中經典的混疊示例
什么是混疊?
根據那奎斯特原理,為了在數字域內復制原始信號,ADC必須至少以輸入信號最高頻率分量的兩倍對輸入信號進行采樣—否則的話,會產生混疊。所需的最小采樣率被稱為那奎斯特速率。或者反過來看,ADC能夠準確轉換的最高頻信號為采樣率的一半,這被稱為那奎斯特頻率。
我們來看一個示例數據采樣系統,在這個示例中,ADC以每秒7個樣本 (SPS) 的速率對6Hz輸入正弦波進行采樣。我們得到的那奎斯特頻率為3.5Hz,對于任何一個頻率大于3.5Hz的輸入信號,會產生原始信號的混疊。圖2顯示的是時間域內,使用6Hz原始輸入,以及其兩個混疊的情況:這兩個混疊分別為1Hz和8Hz。由于全部3個正弦波在每個采樣上相交,所以,以7SPS采樣獲得的6Hz正弦波看上去與1Hz或8Hz的正弦波沒有什么不同!當我們查看輸出數據時,混疊使我們無法將想要測量的6Hz 正弦波與它的混疊波形區分開來,并且所需要的信號內容也丟失了。
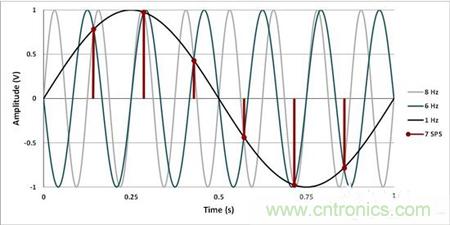
圖2:時間域內的混疊
不過,你怎么能知道6Hz正弦波將會在1Hz和8Hz時出現混疊呢?在頻率域內觀察混疊會使得這一點變得很明顯。當使用ADC進行采樣時,輸入信號的頻率成分,從DC開始,在數倍于采樣率的頻率上重現。現在,你應該明白術語“折返”為什么經常被用來描述信號的混疊方式了—如果你沿著虛線將圖3折疊起來看,這些信號互相之間完美地重疊在一起。
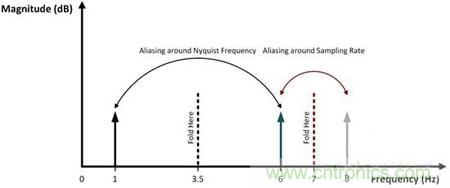
圖3:頻率域內的混疊
為了準確地測量輸入正弦波,采樣率必須滿足那奎斯特采樣標準。在上面的示例中,你需要將采樣率至少增加到12SPS。恰恰在12SPS時,6Hz輸入將仍然折返至DC,并且會在測量值中增加一個偏移,所以,采樣只快了一點點,確保你所需要的信號根本就不會發生混疊。
不過噪聲情況是怎樣的呢?在整個頻率范圍內會出現白噪聲,毫無疑問,白噪聲將從更高頻率混疊返回至DC與那奎斯特頻率之間的通頻帶。產生的是一個更高的帶內噪聲水平,而這會降低信噪比 (SNR) 等重要技術規格的等級。幸運的是,有一個針對此問題的解決方案:那就是抗混疊濾波器。
抗混疊濾波器
大多數ADC之前都會有一個抗混疊濾波器,而這個濾波器與衰減信號(超過了所需帶寬)的低通濾波器沒有什么不同。如圖4所示,一個理想抗混疊濾波器的響應在那奎斯特頻率之前是絕對水平的,在這個頻率之后,它迅速滾降,以衰減帶外頻率。在這里,采樣率已加倍至14SPS,這將7Hz的那奎斯特頻率和原始6Hz輸入安全的放置在通頻帶之內。
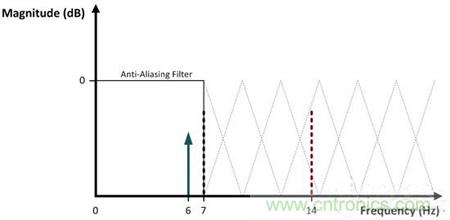
圖4:理想抗混疊濾波器的頻率響應
設計一款能夠實現這種頻率響應類型的濾波器可不是一件容易的事,通常需要有源組件。這些額外的組件會大大增加信號鏈的尺寸、成本和功耗,并且很難達到理想效果。








