中心議題:
- ?多傳感器數據融合技術能對缺陷信號作智能化處理
- ?電磁感應式傳感器和霍爾傳感器的工作原理
- ?采用小波去噪的方法,并利用RBF神經網絡的數據融合技術對缺陷信號進行檢測處理并得出仿真結果
解決方案:
- ?采用漏磁傳感器陣列,提高檢測靈敏度,減小鋼管表面接觸噪聲和溫度影響
- ?對信號預處理,保證測試準確性
- ?選用RBF神經網絡作為融合中心的特征層融合器
隨著電子技術、神經網絡和人工智能處理技術的發展,國內外都在開展新的漏磁信號處理方法的研究。由于傳統方法受人為因素影響嚴重,容易產生漏檢誤檢,大大影響了檢測準確度,因此特別需要一種對缺陷信號的智能化處理方法。多傳感器數據融合技術是近年來形成和發展起來的一種自動化信息綜合處理技術,它充分利用多源信息的互補性和計算機的高速運算能力來提高結果信息的質量。由于多傳感器數據融合可以對來自多個傳感器的數據進行多級別、多方面、多層次的處理,從而產生新的有意義的信息,而這種信息是任何單一傳感器所無法獲得的, 并且它還能有效地消除由于單一類型傳感器失效而引起的誤差,因而多傳感器數據融合在信號處理領域得到了廣泛的關注[1]。本文利用小波閾值降噪算法來突出信號缺陷特征,并將處理后的信號送入RBF神經網絡數據融合中心,利用兩類傳感器之間的信息冗余來提高檢測精度,消除測量中的不確定性,獲得更準確可靠的測量結果。
數據融合傳感器陣列
多傳感器數據融合在運用過程的各階段(例如模型建立、特征提取、目標識別等)需要各種各樣的傳感器。由于沒有哪一類傳感器的各種性能指標都絕對比其他類型傳感器好,因此在一個系統中,需要同時采用多種類型的傳感器,以提高系統檢測、識別、分類和決策能力。本文根據系統的需要使用了兩類傳感器:電磁感應式傳感器和霍爾傳感器,利用它們之間產生的冗余信息進而檢測出缺陷信號。數據融合系統結構如圖1所示。
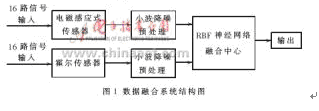
根據缺陷信號的特點以及環境要求,采用漏磁傳感器陣列進行數據采集[2]。為提高檢測靈敏度,減小鋼管表面接觸噪聲和溫度影響,由32個傳感器組成的傳感器陣列,貼敷在與鋼管表面吻合的耐磨塊內,形成探頭。傳感器被分為兩組,每組16個。一組由16個電磁感應式傳感器組成,另一組由16個霍爾傳感器組成,兩組交替分配在探頭表面。傳感器陣列傳送出來的兩組32路信號經過預處理之后被送到融合中心進行數據融合。
電磁感應式傳感器
電磁感應式傳感器的工作原理是:當它貼著鋼管表面掃查時,鋼管缺陷產生的漏磁場會引起穿過線圈的磁通量變化,從而使電磁線圈中產生感生電動勢,形成缺陷信號。當檢測用的電磁線圈與鋼管做相對運動時,檢測漏磁場的線圈所產生的感應電動勢Uc為:

式中,n為線圈匝數,φ為線圈中通過的漏磁場磁通量;B為漏磁場的磁通量密度;S為線圈的橫截面積,t為線圈運動時間。電磁感應式傳感器能夠在很大的溫度范圍中應用,且工作壽命長、抗灰塵、抗水和抗油污的能力強,即能耐受各種環境條件及外部噪聲。
霍爾傳感器
霍爾傳感器檢測漏磁信號的工作原理是:當電流I沿與磁場B的垂直方向通過時,在與電流和磁場垂直的霍爾傳感器兩側便產生霍爾電勢Hr:

式中,RH為霍爾系數;KH為霍爾系數RH與霍爾傳感器厚度t之比,稱為霍爾元件靈敏度。當霍爾系數RH與電流一定時,霍爾電勢Hr只取決于磁場B的強度而與漏磁場的運動速度無關,因此,霍爾傳感器不會受到管線檢測的非勻速性的影響。
信號預處理
對于多傳感器測量的漏磁缺陷信號數據,為了保證測試的準確性,系統取得信號之后,首先要對信號進行預處理,濾除各種外界干擾和各種噪聲,獲得正確的測量粗值。一般有兩種方法:一是進行平滑處理,實際算法可通過滑動中值平滑器來實現;二是剔除粗大誤差,可采取數據相關剔除法與信號平滑法同時進行,將來自多傳感器具有相關性、互補性和冗余性的數據進行數據融合。這種方法可以充分利用被測目標在時間與空間上的信息,對被測量進行精確描述[4]。因此,多傳感器融合的結果比單個傳感器的測量值更為準確。
本文對漏磁缺陷信號使用小波降噪算法,該方法首先將每個傳感器的測量值用小波閾值的方法去噪,以減小噪聲對傳感器測量值的影響。為了更好地重建傳感器信號,可將各個傳感器測量值進行歸一化處理,然后再送入RBF神經網絡的數據融合中心進行融合。對缺陷信號采取小波分析可以突出缺陷點,經過小波分析后可將缺陷信號的局部模極大值及其位置以及漏磁信號的波形特征等作為特征信息,用來區分不同的缺陷。
信號模型
在漏磁信號采集過程中,假設有N個傳感器對同一缺陷的不同位置進行測量,每個傳感器得到的漏磁信號測量值記為Xj(j=1,2,3...N),在測量過程中存在內部和外部噪聲影響,測量值可以表示為:
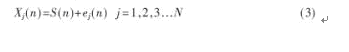
式中,S(n)為真實的被測量值,ej(n)(j=1,2,3...N)為第j個傳感器在n時刻的加性噪聲,Xj(n)為第j個傳感器在n 時刻的實際測量值。由于每個傳感器受到噪聲干擾的程度不同,所以實際測量值偏離真實的被測量值的程度也是不同的。
小波閾值去噪
小波去噪的方法主要通過設置閾值來實現,對漏磁信號的離散小波變換,計算所有小波系數,剔除被認為與噪聲有關的小波系數,然后通過小波變換的逆變換得到信號。對于給定的信號,選取閾值的方法很多,本文使用的是基于Stein無偏風險估計值最小化(SURE)的方法:
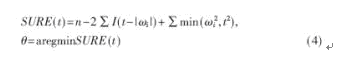
式中的閾值t,得到它的是似然函數,然后使似然函數最小化,得到所需閾值。在VISU的方法中閾值的選取固定不變,而在SURE方法中,閾值是自適應變化的,可以更好地降低噪聲對缺陷信號的影響[4]。根據經過小波處理后的漏磁信號缺陷波形,可以提取出缺陷的特征向量,用以作為神經網絡融合中心的輸入。數據融合可根據融合的層次和實際內容將其分成像素層融合、特征層融合和決策層融合。本文把經過小波降噪處理后的信號通過RBF神經網絡融合中心進行特征級融合,以對信號進行定量分析。
RBF神經網絡融合算法
常用的數據融合方法包括神經網絡、聚類算法或模板法。其中,人工神經網絡具有學習、記憶、聯想、容錯、并行處理等卓越功能,在拓撲結構、權重自適應等方面應用靈活,已在計量測試儀器標定、故障診斷中獲得廣泛應用。在多傳感器測量系統中,采用數據融合技術可為系統帶來多方面的益處[5],如增強系統的穩定性、增加系統的可信度及提高系統的檢測能力。由于BP神經網絡收斂速度慢,網絡訓練時間較長,且存在局部極小值的問題,RBF神經網絡比BP神經網絡具有更快的學習特征,其逼近能力更強。因此,本系統選用RBF神經網絡作為融合中心的特征層融合器進行融合訓練。
RBF神經網絡結構
RBF神經網絡結構圖如圖2所示,第一層為輸入層,用作特征信息融合信息采集,構成輸入樣本空間X;第二層為隱含層,用作將輸入樣本空間映射為高維的徑向基函數空間,即對輸入信息空間X進行特征提取。隱含層節點參數向量包括中心值Ci和標準偏差δi;第三層為輸出層,ωi為第i個基函數與輸出節點的連接權值,輸出為Y,徑向基函數選擇高斯函數,如下:
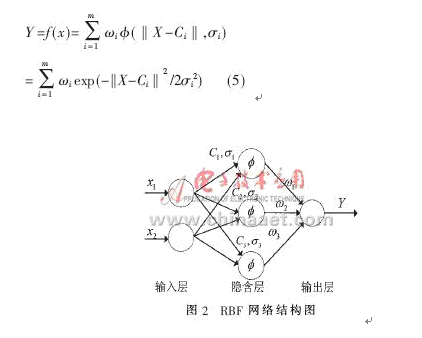
式中,m為隱含層節點數, ‖•‖為歐幾里德范數。
RBF神經網絡學習過程分為兩個階段:第一階段,根據所有的輸入樣本確定徑向基函數及其參數,即確定隱含層各節點的高斯函數的中心值和標準偏差;第二階段,在確定隱含層各參數后,根據樣本,采用梯度下降算法,求出輸出層的權值。
RBF神經網絡算法主要是通過調整連接權值,使輸出層與期望輸出逐漸趨于一致。根據最小均方差原理(MSE),當誤差指標處于某一個范圍之內時,則可以停止運算,表示網絡訓練成功。
神經RBF網絡參數選取及權值更新
在融合中心,RBF神經網絡的結構參數有徑向基函數的隱含層節點數、中心值和標準偏差。節點數越多,學習能力越強,合理的節點數可通過訓練得到最佳值。確定中心值和標準偏差可采用簡單有效的聚類算法K-均值聚類算法。該方法具有實現簡便、運算量較小、抗噪聲能力強以及識別率高等優點,可以很好地解決建模樣本分布不合理的問題。標準偏差的大小影響徑向基函數對輸入的響應,標準偏差太小則基函數只能對輸入數據附近的很小區域做出響應,標準偏差過大則可能丟失固有的局部信息,模型精度也較差,因此標準偏差的選取應在一個穩定區間內進行。
本文利用梯度下降算法確定連接權值。假設總誤差為:
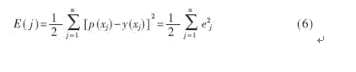
式中,p(xj)為第j個訓練樣本的期望輸出;y(xj)為網絡實際輸出,n為訓練樣本總數。
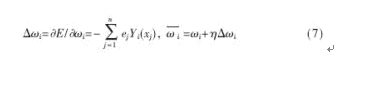
式中,Yi(xj)為隱含層第i個基函數的輸出; 為連接權值ωi的更新值;η為學習步長,一般為在0.2~0.9之間選取[7]。
實驗仿真分析
本文采用MATLAB軟件進行仿真實驗,通過提供的40組人工裂縫的樣本,對RBF神經網絡系統進行訓練學習和模式識別,并在學習初期對輸入數據進行了預處理,通過樣本訓練逐漸生成最佳的RBF期網絡[8]。另取10組測試樣本數據作為輸入,用MATLAB軟件進行模擬仿真,同時利用RBF神經網絡對其進行深度評估,并與常規BP神經網絡進行對比,其實驗仿真結果如表1所示。
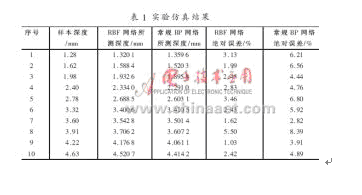
仿真實驗結果表明:利用RBF神經網絡融合能比較精確地檢測到信號缺陷深度,在學習能力和檢測精度上,RBF神經網絡均優于常規BP神經網絡,該方法的平均絕對誤差一般為2.69%,而常規BP神經網絡的平均絕對誤差為5.47%。可見,前者檢測效果明顯好于后者。
在漏磁缺陷信號中,利用小波降噪預處理可以在有效降低噪聲影響的同時,最大程度上保留了缺陷的特征信息;采用漏磁傳感器陣列,一定程度上克服了原有單傳感器系統的檢測誤差;基于RBF神經網絡的漏磁信號數據融合處理,可對裂紋深度檢測的同時進行定量分析。實驗結果表明,RBF 神經網絡不僅具有很快的學習速度, 而且能夠有效地提高檢測的精度和準確率,消除信息的不確定性,提高傳感器的可靠性。






