中心議題:
- 設計傳感器的動力學振動系統
- 討論該系統參數的選取
- 分析模擬傳感器的性能
解決方案:
- 通過改變硅片厚度和彈性臂寬度來設計不同彈性系數和振動系統的固有頻率
- 通過檢測光纖中接收光強的變化獲取反光膜位置的變化
- 設計結構簡單實用的一維振動系統
引 言
動力學振動系統是眾多慣性傳感器中的重要組成部分,其參數的選取決定了傳感器的性能的優劣。針對基于菲涅耳衍射微透鏡的新型光學加速度傳感器設計了一種簡單實用的敏感加速度的振動系統,它是由一個微彈性機械結構連接在外框架上構成。微彈性機械結構不僅是微型加速度傳感器重要組成部分,而且,在微型驅動器、微位移計、微陀螺儀及其他慣性傳感器中也有著重要的應用,在微機電系統(MEMS)中發揮著重要的作用。目前,MEMS中類似于微彈性機械結構的敏感裝置主要有硅懸臂梁、直角彈性結構及結構更復雜的硅彈簧等。微彈性機械結構是在一塊硅片上通過簡單的MEMS工藝加工的,可以通過改變硅片的厚度和彈性臂的寬度來設計不同的彈性系數和振動系統的固有頻率,以滿足傳感器的要求。具體討論了微彈性機械結構參數的選取,并且,模擬分析了傳感器的性能和誤差。
傳感器動力學系統的工作原理
如圖1所示,把一個反光膜平行地置于菲涅耳衍射微透鏡(以下簡稱“微透鏡”)的一側,固定一個敏感加速度的微質量于反光膜后面,光纖端部置于微透鏡的匯聚點處。光的發射和接收可由同一根光纖來完成,則光纖接收光強的大小隨反光膜位置的變化而改變。因此,通過檢測光纖中接收光強的變化可以獲取反光膜位置的變化。
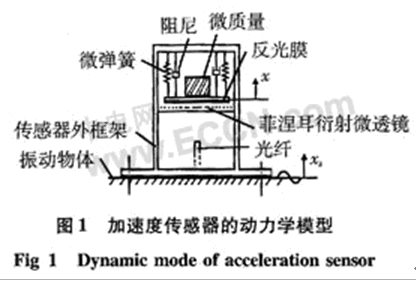
微彈簧一端與反光膜固定連接,另一端固定在傳感器的外框架上,這就形成了一個由微質量、反光膜、微彈簧和外框架構成的振動系統。
把傳感器固定在被測物體上,設被測物體的振動方程為xs=asinωt,令Y表示反光膜相對于微透鏡的穩態響應的振動幅值,則
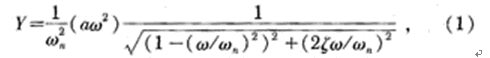
式中a為常數;ω為被測物體的振動頻率;ωn為該振動系統的一階固有頻率;ζ為阻尼比。當ωn》ω時,式(1)可以改寫為

式中aω2為被測物體的加速度幅值。可見只要固有頻率遠高于被測物體的振動頻率,反光膜與微透鏡間的相對運動的振幅Y正比于被測物體的加速度幅值aω2。而振幅Y可由檢測光纖接收的光強來實現獲取,從而通過檢測光強的變化來實現加速度的測量。
動力學系統的設計
a.結構設計
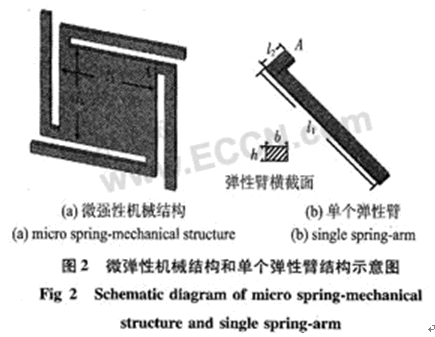
針對這種新型MEMS光學傳感器對動力學系統的要求,設計了一種結構簡單實用的一維振動系統,它包含傳感器中的微彈簧、反光膜和微質量。它是由一個微彈性機械結構(以下簡稱“微結構”)的4個臂端固定在外框架上構成,微結構如圖2(a)所示,它的四周是4個完全相同的彈性臂,相當于傳感器中的微彈簧,單個彈性臂如圖2(b)所示。微結構與微透鏡相鄰的一側蒸鍍上一層鋁或銀構成了傳感器中的反光膜。整個微結構的當量質量相當于傳感器中的微質量。微結構的厚度與彈性臂的寬度可以根據彈性系數和振動系統固有頻率的要求來選擇。整個微結構可在一塊光滑等厚的硅片上通過光刻、深反應離子刻蝕(DRIE)、金屬膜蒸鍍等幾步完成。
b. 參數設計
彈性系數
由于該微結構具有對稱性,對于彈性系數的分析可以把其中的一個臂分離出來做靜力分析。這里,先用能量法來求集中力下單個彈性臂的線性位移。
假設在微結構的中心點處施加一個與微結構表面垂直的集中力4F,則每個彈性臂與中心部分相連的A點受到一個大小為F的集中力,A點位置如圖2中所示。這時彈性臂截面的軸力和剪力引起的變形很小,可以忽略不計,主要是彎矩和扭矩引起的變形。因此,每個彈性臂在集中力F的作用下,產生的總變形位能是
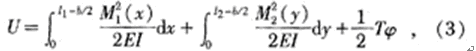
式中 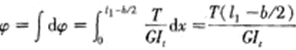 為l1桿的轉角;It為相當極慣性矩,當h≥b時,It=βhb3,β由h/b的數值決定,當h
為l1桿的轉角;It為相當極慣性矩,當h≥b時,It=βhb3,β由h/b的數值決定,當h
在集中力F的作用下A點的彈性位移為

由式(3)、式(4)可以得到微結構4個彈性臂總的彈性系數公式為
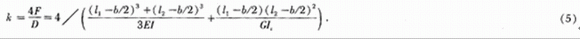
為驗證理論的正確性,同時,用有限元模擬工具AN-SYS對彈性臂進行數值模擬,各參數取值為:F=1 ×10-4N,E=1.69×1011N/m2,G=7.26 ×1010N/m2,l1=2600μm,l2=400μm,b=200 μm,h=200μm,可得到單個彈性臂在A點受到集中力F的作用下的位移為0 0244μm。因此,彈性系數數值模擬值k=4 × 10-4/2.44×10-8=1.64×104(N/m),而由式(5)代入上述參數可得理論分析值k=1.63 ×104N/m,兩者相對誤差為0.6%。
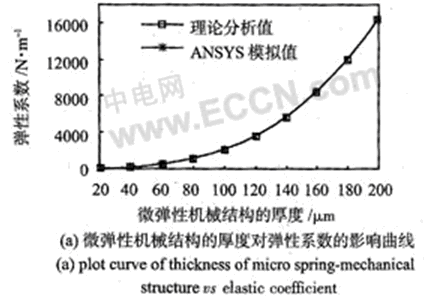
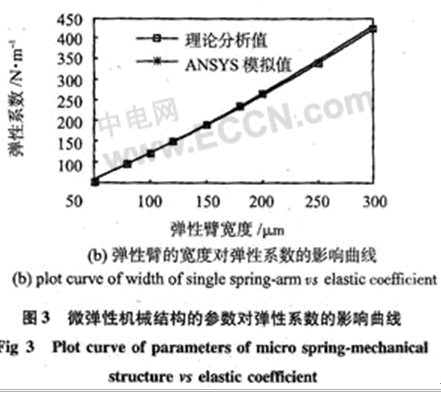
分別用理論方法和ANSYS數值模擬方法得出了在b=200μm時彈性系數k隨微結構厚度h的變化情況,以及在h=50 μm時彈性系數k隨彈性臂寬度b的變化情況,分別如圖3(a),(b)所示。圖3(a)中,2種計算方法求出的彈性系數的平均相對誤差為0.86%,圖3(b)中平均相對誤差為1.06%。可見2種方法計算出來的結果基本吻合。從上述分析可知,在彈簧臂總長確定的情況下,彈簧的彈性系數取決于微結構的厚度h和彈性臂的寬度b,而且,和6的關系近似于線性,因此,可以根據動力學系統的具體要求和加工的工藝性能來選擇合理的h和b,從而滿足傳感器整體性能的要求。
一階固有頻率
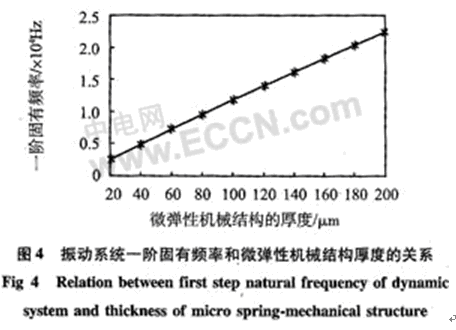
振動系統的固有頻率公式為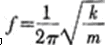 ,m為微結構的當量質量,這里面含有每個彈性臂簡化到A點的等效質量,鑒于等效質量求出來誤差較大,僅用有限元模擬工具ANSYS對振動系統進行模態分析。模擬中,取硅的密度為ρ=2330 kg/m3,l3=l4=2000μm參數含義如圖2所示,其余取上述給定的數值,則振動系統的一階固有頻率為22.37 kHz,在垂直于微結構平面的方向上振動。同時,模擬出了彈性臂寬度b=200μm時,一階固有頻率f和微結構厚度h的關系圖如圖4所示。可見振動系統的一階固有頻率和微結構的厚度h近似地保持線性的關系。
,m為微結構的當量質量,這里面含有每個彈性臂簡化到A點的等效質量,鑒于等效質量求出來誤差較大,僅用有限元模擬工具ANSYS對振動系統進行模態分析。模擬中,取硅的密度為ρ=2330 kg/m3,l3=l4=2000μm參數含義如圖2所示,其余取上述給定的數值,則振動系統的一階固有頻率為22.37 kHz,在垂直于微結構平面的方向上振動。同時,模擬出了彈性臂寬度b=200μm時,一階固有頻率f和微結構厚度h的關系圖如圖4所示。可見振動系統的一階固有頻率和微結構的厚度h近似地保持線性的關系。
傳感器性能分析
由于光纖接收的光強隨反光膜位置按照正弦規律變化,并且,周期為λ/2,因此,必須為反光膜選擇一個合適的工作點和工作區間。另外,考慮傳感器靈敏度、加速度測量范圍、頻率范圍和加工工藝等因素,作如下配置:用λ=632.8 nm的單色光作為光源,選定反光膜所在的線性最好的點為工作點,反光膜的振動范圍dm=20 nm,其他參數值均取上述的模擬值,由胡克定律F=kdm、牛頓第二定律F=mam和振動系統的一階固有頻率公式 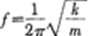 可以求出傳感器的量程約為±395 m/s2,測量頻率范圍取動力學系統固有頻率的20%,約為1~4.5 kHz,上述am為傳感器的加速度量程。
可以求出傳感器的量程約為±395 m/s2,測量頻率范圍取動力學系統固有頻率的20%,約為1~4.5 kHz,上述am為傳感器的加速度量程。
由式(1)、式(2)可知,實際測量中存在著一個誤差因子δ,即
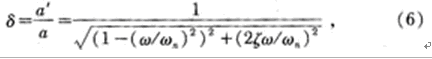
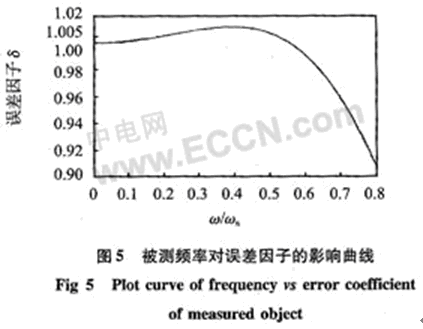
式中a′和a分別為加速度的測得值和真實值。δ和阻尼比ζ與被測物體的頻率ω有關,當ζ=0.65~0.07時,ζ最接近1,因此,取ζ=0.65進行計算機模擬,結果如圖5所示。可以看出:被測頻率比較小的時候測得的加速度值更接近于真實值,當ω/ωn=0.2時,ζ=1.0054,因此,傳感器在設定的頻率范圍1~4.5 kHz的誤差不大于0.54%。
結論
設計了傳感器的動力學振動系統,并對參數的選取進行了討論分析,最后,分析模擬了傳感器的性能。改變微彈性機械結構的參數可以得到不同性能的傳感器,對眾多的慣性傳感器和其他MEMS設計具有指導意義。







