【導讀】將模擬傳感器信號轉換至數字領域是可穿戴式病人監護設備的標準做法。但設計人員需注意,這些應用要依賴一個系統,這個系統即使在噪聲環境中依然可產生可靠、可重復的結果。噪聲濾波技術是這種解決方案電路的關鍵部分。
過去,濾波過程只存在于模擬領域。最近,隨著微控制器和更復雜信號處理器的出現,人們迫切希望將濾波功能悉數轉移至數字領域:但買家需謹慎。這種做法有利也有弊。
本文簡述了模擬領域和數字領域噪聲濾波的優缺點。本文通過兩個設計示例來討論每一種濾波方法。第一種設計,采用 STMicroelectronics TSX7191IYLT 低功耗、精密、軌至軌、9.0 MHz 運算放大器實現模擬低通濾波器。
第二種設計,采用 Microchip Technology PIC18LF25K40T-I/MV 低功耗、高性能、采用 XLP 技術的微控制器實現編碼式有限脈沖響應 (FIR) 濾波器。
模擬與數字濾波之比較
模擬濾波方法在模數轉換器 (ADC) 之前使用低通或抗混疊濾波器。在 ADC 之前增加濾波功能可以有效減少干擾噪聲,但會增加成本,占用電路板空間(圖 1)。
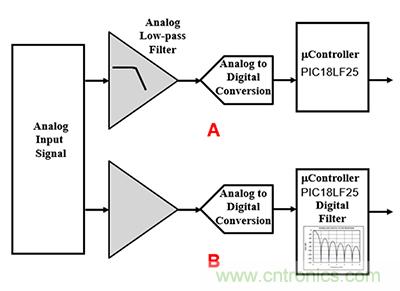
數字解決方案在 ADC 后使用平均法減少噪聲。基本上可以“隨意”向處理器編碼添加濾波功能,因為電路中的處理器已經執行其他功能。就編碼時間而言,數字濾波功能僅占用少量的資源,但數字濾波存在一個很明顯的缺點,那就是其衰減混疊信號的能力不足。
奈奎斯特定理
幾乎所有的信號轉換和濾波論述均會提及奈奎斯特定理,亦稱為采樣定理。該定理涉及 ADC 的數字化過程,規定 ADC 的采樣率須至少達到采樣信號頻率的兩倍,否則將產生混疊。采樣率是轉換器采樣、采集、數字化和準備下一次轉換所需的時間。也稱為轉換器的吞吐率。
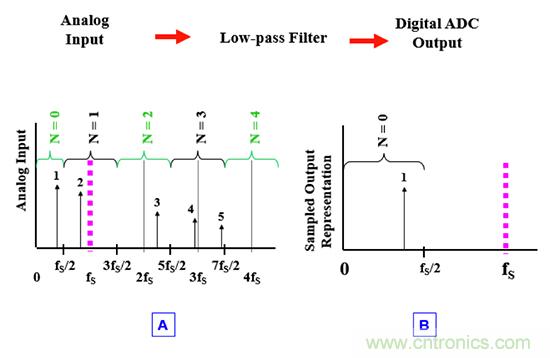
通過多個采樣,ADC 可以準確地重現模擬輸入信號的幅度,但根據 FALIASED = |fIN – Nfs| 公式可得出,頻域也會有所變化,高出 ADC 采樣頻率的 ½(圖 2)。
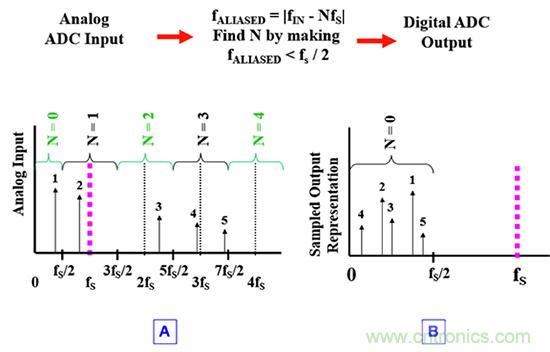
在 ADC 之前,ADC 的采樣頻率 (fS) 決定了奈奎斯特分頻(圖 2A)。N = 0 時,頻率范圍是 DC 至 fS/2。N = 1 時,頻率范圍是圍繞 fs 進行 ± fS/2 波動。N = 2 時,頻率范圍是圍繞 2fs 進行 ± fS/2 波動。這種模式會隨著頻率不斷增長繼續下去。模擬頻率范圍的劃定決定了數字化后的信號頻率分布。
例如,模擬信號通過 ADC 數字化后,可以完整地保留信號 1 的幅度和頻率(圖 2B)。這是因為信號 1 的頻率在 DC 和二分之一采樣頻率 (fS/2) 之間。但對于信號 2 至 5,ADC 轉換不再保留模擬輸入至數字輸出的頻率關系。
就上述所有情況而言,ADC 轉換在理想情況下可以保留信號幅度。信號 2 的頻率轉換等于 |f2 – fS|,其中 f2 是信號 2 的頻率。請注意,在數字領域,f2 比 fS/2 更接近于 DC。
信號 3 的頻率轉換等于 |f3 – 2fS|,其中 f3 是信號 3 的頻率。請注意,在數字領域中,f3 是 DC 和 fS/2 的中間值。同理,信號 4 的頻率轉換等于 |f4 – 3fS|,其中 f4 是信號 4 的頻率。請注意,在數字領域中,f4 非常接近于 DC。信號 5 的頻率轉換等于 |f5 – 3fS|,其中 f5 是信號 5 的頻率。請注意,在數字領域中,f5 非常接近于 fS/2。
頻率豐富的模擬信號經過 ADC 后,數字輸出后的頻率仍然非常豐富,但頻率均無規則地分布在 DC 和 fS/2 之間。無法恢復初始頻率特征,也無法進一步分辨“好信號”和“差信號”。
模擬低通濾波器
解決以上問題的簡易解決方案是在信號鏈路中加入模擬低通濾波器。濾波器置于 ADC 的輸入位置。低通濾波器會衰減掉較高頻率的信號。低通濾波器的通用頻率響應允許較低頻率信號通過,同時會衰減高頻率信號(圖 3)。
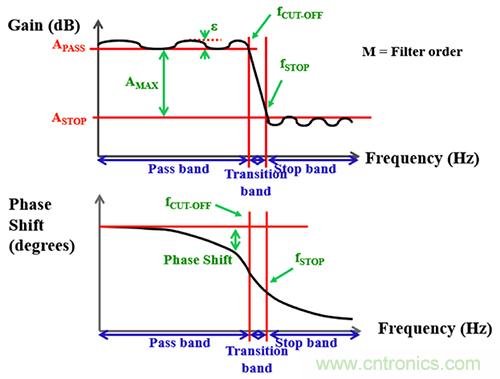
通頻帶區域的增益曲線平緩或略有波動。在 fCUT-OFF 或通頻帶區域末端,濾波器開始進入過渡帶。信號衰減速度或衰減率取決于濾波器逼近類型和濾波器階數。濾波器逼近類型示例:
● 貝塞爾
● 巴特沃斯
● 切比雪夫
● 反切比雪夫
● 傳統高斯
● 線性相位
低通濾波器階數定義了極數。例如,4 階濾波器有四個極,表示在電路中有四個電容器。
低通濾波器可通過不同方式實現。常見的實現方法是 Sallen-Key 和多反饋 (MFB) 電路(圖 4)。
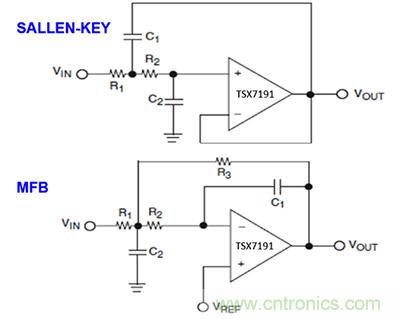
Sallen-Key 低通濾波器增益的實現是非反相。低通 MFB 增益總是反相的。
用于這些電路的相關放大器類型具有皮安偏置電流、低補償電壓(<1 毫伏 (mV))和相當于 100 倍 fCUT-OFF 的帶寬。單位增益 Sallen-Key 關鍵濾波器需要具有輸入和輸出、軌至軌運算的放大器。TSX7191IYLT 符合這些準則。
如果將一個轉折頻率接近 fS/2 的 4 階模擬低通濾波器插入圖 1A,圖 2 中的較高頻率信號將出現衰減。所產生的響應基本可以消除之前的混疊信號(圖 4)。
第二種濾波方法是用數字濾波器代替模擬濾波器。
數字有限脈沖響應 (FIR) 濾波器
自信過頭的控制器和處理器設計人員認為,他們可以解決數字領域中的所有問題,他們普遍認為:“無論什么信號,我都能通過數字手段進行處理。”在數字領域確實可以做很多處理,但并不是萬能的。
控制器或處理器設計人員傾向于認為,FIR 是適用于此用途的數字濾波器。FIR 濾波器大體來說是一種加權平均濾波器,隨時間推移能夠衰減高頻噪聲。這種濾波器沒有反饋回路,穩定性強(圖 6)。
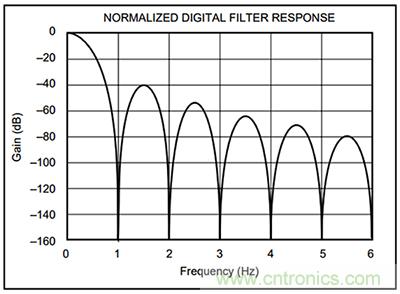
FIR 數字濾波器計算采用線性逼近方式(圖 7)。
如果 N 是抽頭數,則 N 抽頭的濾波器系數是 a0, a1, … aN-1。
FIR 數字濾波器有線性相位響應。具體是指相位在通過濾波器時無失真。實現簡單,因為通常有信號指令循環。
FIR 濾波器還具有令人滿意的數字特性。因為沒有反饋,FIR 濾波器只需使用較少比特,非理想算術問題也更少。
對比兩種濾波器
數字 FIR 濾波器極具吸引力。可以聯機編程,能夠實現不同的功能,比如 IIR,甚至是與模擬濾波器功能同等。在故障排除階段,可以輕松獲得低成本解決方案。
數字濾波器的優點極具吸引力,但有一個根本問題。ADC 向信號路徑中混疊了有害信號。因此,數字濾波器要從混雜信號入手。
而模擬解決方案可以處理這一問題。這種方法旨在盡快消除問題。
總結
將模擬傳感器信號轉換至數字領域是可穿戴式病人監護設備的標準做法。這些設備極其依賴可靠、可重復的結果。在這些設計中,很重要的一項決策是判斷是模擬濾波合適,還是數字濾波合適。
本文評估了數據采集系統中模擬濾波器和數字濾波器的區別。模擬解決方案在數字化操作之前使用低通或抗混疊濾波器。該解決方案可以成功地衰減 ADC 數字輸出信號結果中可能出現的混疊信號。
該數字系統在完成信號數字化后使用 FIR濾波器。該解決方案采用平均技術減少噪聲。但無法區分頻帶中混疊信號與信號。模擬濾波器是兩種方法中較好的選擇。
免責聲明:本文為轉載文章,轉載此文目的在于傳遞更多信息,版權歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權問題,請聯系小編進行處理。
推薦閱讀:






