從數學原理上來說,通用型有源濾波器可以用如下的系統框圖來表示。
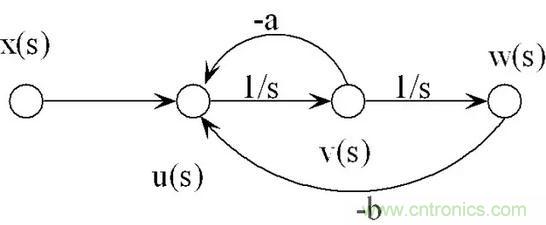 圖1:典型的二階系統的信號流圖
圖1:典型的二階系統的信號流圖
上面是一個典型的二階系統的信號流圖,利用Mason 公式可以很容易的得到系統各個通路的傳遞函數:
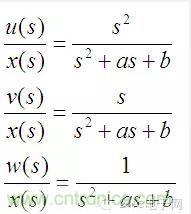
上面三個式子分別對應高通、帶通和低通濾波器,如果將u、v、w三路信號加權疊加則可以組成任意的二階系統。
二階系統傳遞函數的分母多項式的標準形式為:
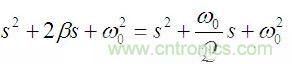
經比較可知,大環路增益b決定二階系統的固有頻率,小環路的增益a決定系統的阻尼系數,也就是決定系統的品質因數Q。
狀態變量濾波器
狀態變量濾波器也被稱為KHN 濾波器,屬于通用型有源濾波器的一種實現形式,由Kerwin、Huelsman’Newcomb與1967年提出的。電路的基本形式如下。
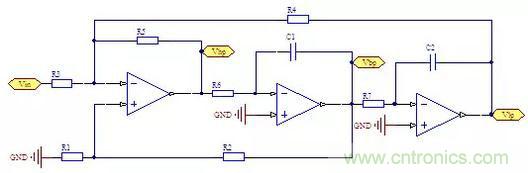
圖2:反向輸入型KHN 濾波器
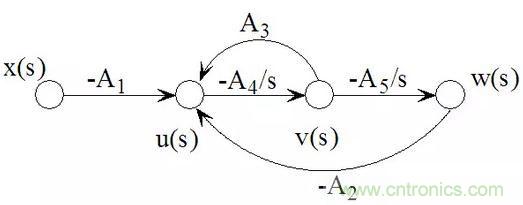
轉換為信號流圖后如下圖所示。
其中:
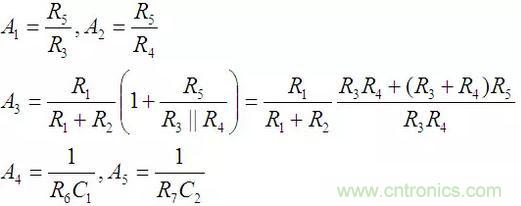
列寫系統各個通路的傳遞函數如下:
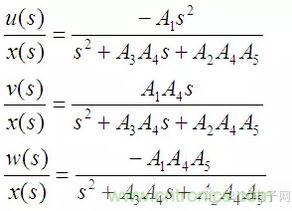
將(3)帶入(4)后經整理可得:
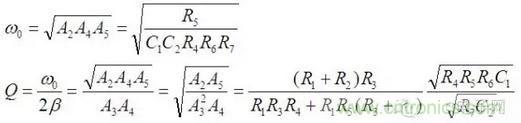
如果對電阻電容的值做一些限制,公式會變得更簡單。設:

可以看出品質因數Q只依賴于R1與R2的比值。而固有頻率只與RC的乘積有關。

正向輸入型的KHN濾波器如下圖所示:
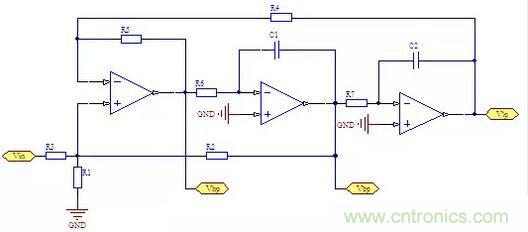
圖3:正向輸入型的KHN濾波器
對應的信號流圖如下:
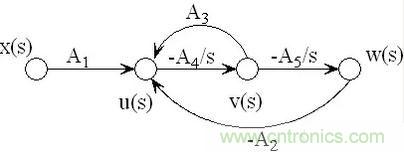
從信號流圖上看,僅僅是x(s) 到 u(s) 之間的增益從 -A1 變為 A1,其他的地方完全相同。但是由于R3從運放的負輸入端移動到了正輸入端,所以A1和A3的值發生了很大的變化。

列寫系統各個通路的傳遞函數如下:
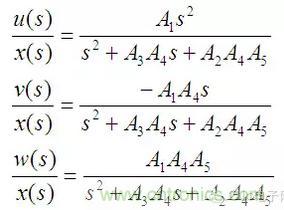
由于A2、A4和A5都沒有變化,所以系統的固有頻率沒有變:

如果還是做一些限制:
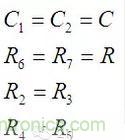
則可以簡化為:
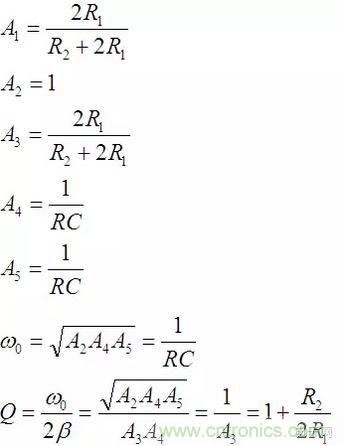
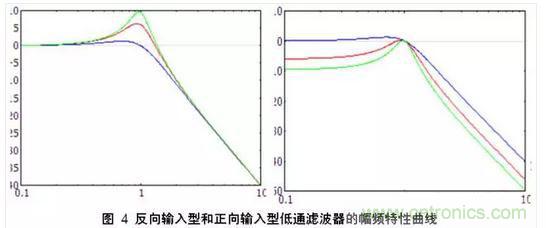
正向輸入型和反向輸入型最大的區別在于通頻帶的增益。下面給出低通濾波器時的幅頻特性曲線。兩邊的曲線一對比他們的區別就一目了然了。
Tow-Thomas 型二階濾波器
另一種類似的電路形式稱之為 Tow-Thomas 型濾波器。它的基本電路形式如下,其中R3=R6構成一個反向器。
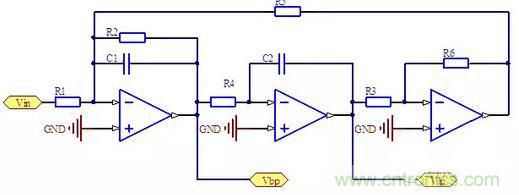
圖5:Tow-Thomas 型濾波器
信號流圖與正向輸入型KHN濾波器完全相同。需要說明的是u(s)是電流信號,表示的是流過C1的電流的大小。
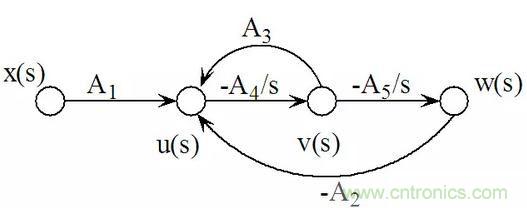
但是A1到A5的表達式卻變得簡單的多。
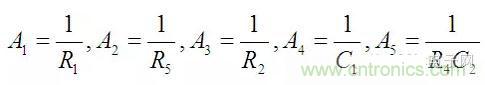
列寫系統各個通路的傳遞函數也與正向輸入型KHN濾波器完全相同,這里重復如下:
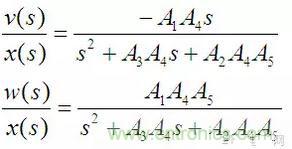
由于u(s)是電流信號,無法直接引出使用,因此也就沒有列出來。將(16)帶入(17)后可得:
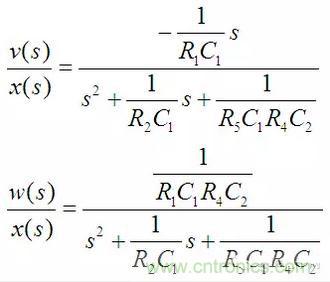
品質因數和固有頻率計算如下:

則可以化簡為:
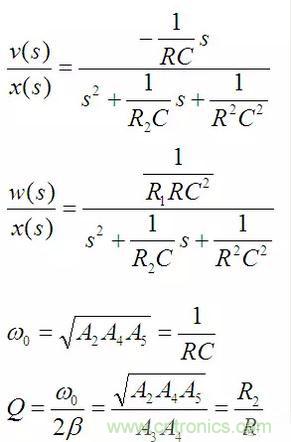
原始信號減去帶通信號就稱為帶阻信號了,因此再增加一個運放就可以實現帶阻型濾波器。
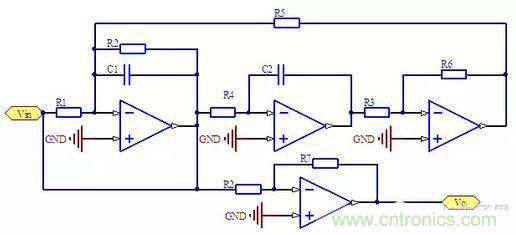
圖6:Tow-Thomas 帶阻型濾波器
這個電路的要點是R1=R2,這樣才能保證原始信號與帶通信號的幅度相同。也就是說要求A1=A3。
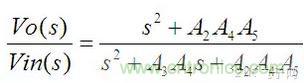
簡單的說,這種辦法生成的帶阻濾波器其實就是在虛軸上對應位置添加了零點。
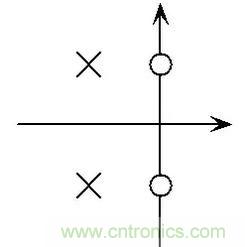
圖7:Tow-Thomas 帶阻型濾波器的零、極點分布
帶阻信號如果再與低通信號相加,就能夠組成低通帶阻型或高通帶阻型。下面是電路原理圖。
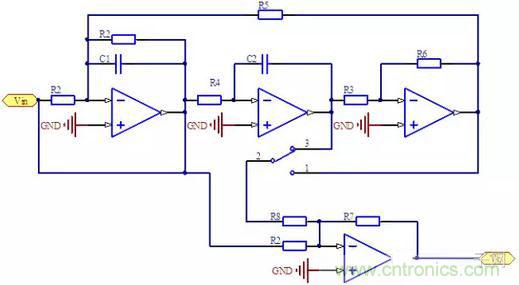
圖8:Tow-Thomas (高通/低通)帶阻型濾波器
單刀雙擲開關打到3的位置時對應低通帶阻濾波器,打到2的位置時對應高通帶阻濾波器。原理可以這樣分析。首先,傳遞函數可以寫為如下形式:
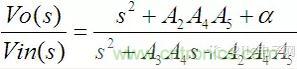
單刀雙擲開關打到3的位置時α的值為正,打到2的位置時α的值為負。α 值的變化對應的是系統零點的移動。α大于0 相當于零點互相遠離。
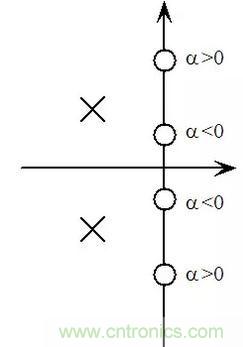
圖9:Tow-Thomas (高通/低通)帶阻型濾波器的零、極點分布
(高通/低通)帶阻型濾波器的典型頻響如下面兩幅圖所示。
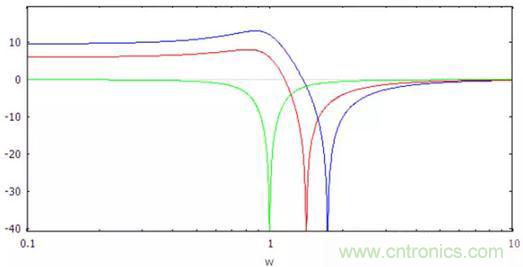
圖10:低通帶阻型濾波器的幅頻響應
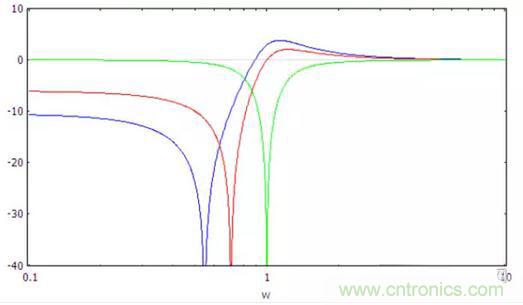
圖11:高通帶阻型濾波器的幅頻響應








