【導讀】在電路應用中由于存在電感電容等無源器件,在頻率信號作用下,電容充放電,電感儲能釋放能量的過程,輸入輸出信號就存在相位的變化。對于電容移相的過程,是由于電容器的充放電引起電路的交變電流。
在電路應用中由于存在電感電容等無源器件,在頻率信號作用下,電容充放電,電感儲能釋放能量的過程,輸入輸出信號就存在相位的變化。對于電容移相的過程,是由于電容器的充放電引起電路的交變電流。產生電流周期比電壓周期超前九十度。而電感則是由于自感電動勢始終阻礙自變量的變化的特性,移相情形正好與電容相反。一接通電路,一個周期開始時電感端電壓最大,電流最小,一個周期結束時,端電壓最小,電流量大,得到的是一個電壓超前90度的移相效果。簡單的模擬電路使用的移相電路就是RC移相和LC移相。一般多使用RC的移相電路。下圖表示的是RC的積分微分電路,會實現輸出信號超前滯后輸入的波形。
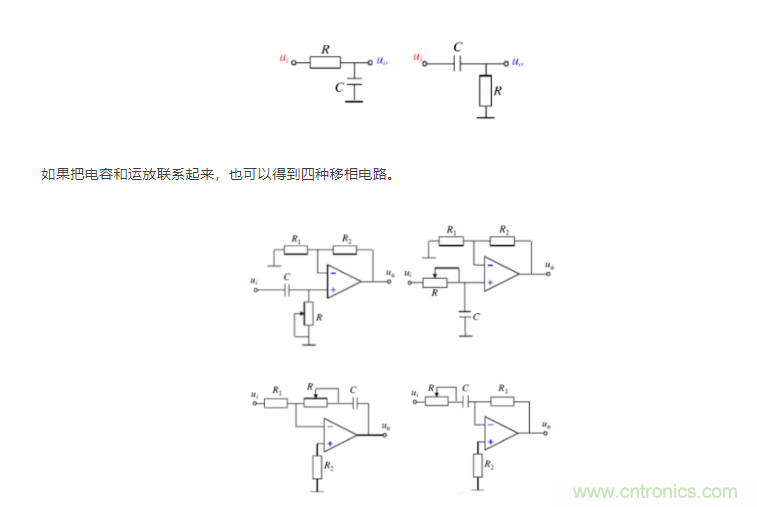
分別是可以實現0-90、270-360、90-180、180-270移相的目的。那么在不同的輸入信號頻率f情況下,相移會是多少呢?幅值會是多少呢?對于同樣的移相電路對于不同的輸入信號頻率的移相角度是不同的。如果使用仿真軟件是很容易得到Bode圖,從而得到幅頻曲線和相頻曲線的。那么在不
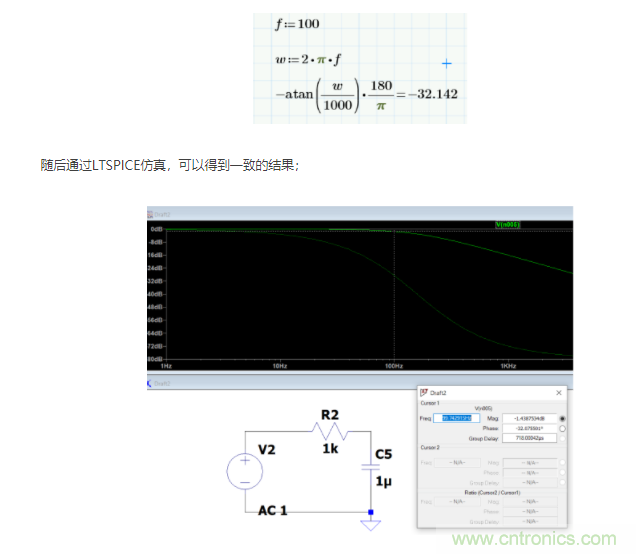
繪制伯德圖的情況下,應該如何計算?下圖是簡單的RC低通濾波器:對于這種低通濾波器,其傳遞函數為下面先通過一個簡單例子說明,如何計算移相的相位。如果系統的傳遞函數為:可以知道系統的響應函數y(t)是由輸入x(t)=cos2t和x(t)=cos(10t-50)的激勵下得到的。將s=jw替換,可以得到:因此傳遞函數的模為:傳遞函數的相位角為:所以只要知道了傳遞函數,和輸入信號的頻率,就可以知道在輸入信號的作用下,輸出信號衰減的幅值和移動的相位角。對于上圖中的RC低通濾波器,通過計算得知,當輸入信號頻率f=100Hz的時候,相移是滯后32.142°;

隨后通過LTSPICE仿真,可以得到一致的結果;
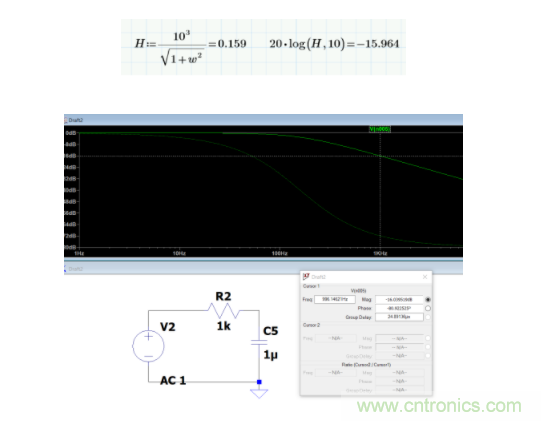
輸出信號的幅值可以通過如下公式計算,計算和仿真是接近的,計算得到的是-15.964dB,仿真得到的是-16.03dB.
現在看一個稍微復雜的電路,全通濾波器進行分析。全通濾波器由一階全通濾波器和二階全通濾波器組成,只需要一個運放。先看下圖的一階全通濾波器(低通)。
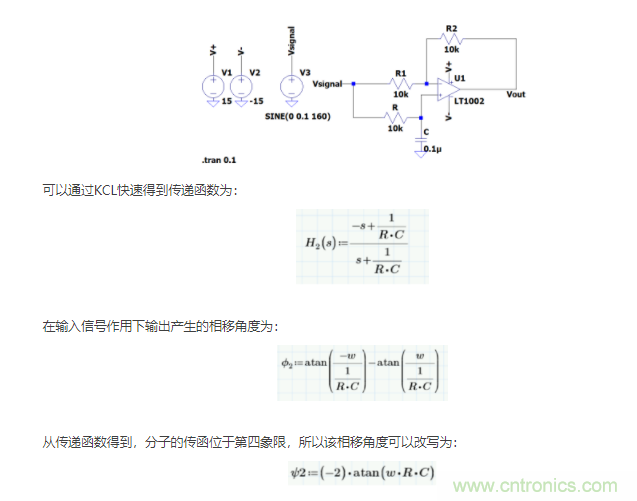
從該結果中可以得到,當輸入信號f=0Hz,是沒有相移的;輸入信號w=1/RC,相移是90;輸入信號f是高頻的時候,相移是180;利用LTSPICE仿真可以得到輸出滯后輸入90。利用計算和仿真也能得到一樣的結果。

下圖也是一階全通濾波器(高通),由于傳遞函數不同,所以可以得到和低通不一樣的特性。
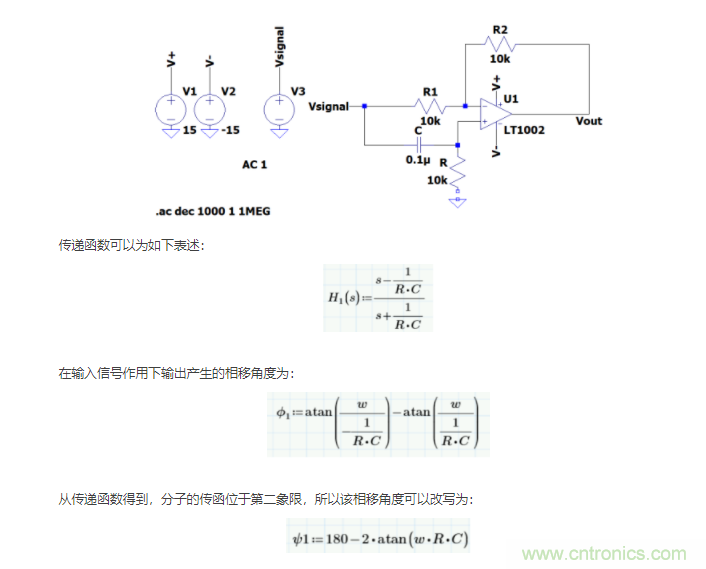
從該結果中可以得到,當輸入信號f=0Hz,相移超前180;輸入信號w=1/RC,相移是超前90;輸入信號f是高頻的時候,相移是0;仿真結果也是和計算結果一致。

免責聲明:本文為轉載文章,轉載此文目的在于傳遞更多信息,版權歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權問題,請電話或者郵箱聯系小編進行侵刪。








