【導讀】想要測量諧振器的Q因子并不少見??赡苄枰_定其在耦合諧振濾波器中的適用性,或者評估RFID標簽的性能。通常,此測量是通過非常輕的輸入和輸出耦合進行的,以減小50-Ω源阻抗和負載阻抗的負載效應。
想要測量諧振器的Q因子并不少見??赡苄枰_定其在耦合諧振濾波器中的適用性,或者評估RFID標簽的性能。通常,此測量是通過非常輕的輸入和輸出耦合進行的,以減小50-Ω源阻抗和負載阻抗的負載效應。
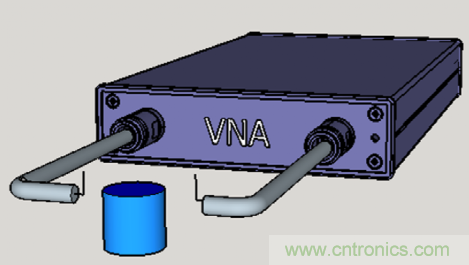
圖1
1.對于諧振器的2端口Q測量,請建立非常輕的輸入和輸出耦合,以減小50Ω源阻抗和負載阻抗的負載效應。
到諧振器的耦合和從諧振器的耦合可以用兩個電短路的天線或回路耦合到諧振器的電場或磁場來實現(圖1)。可以進行這種測量的一種儀器是CopperMountainTechnologies的TR1300/1,這是一種1.3GHz矢量網絡分析儀(VNA)(圖2)。

圖2
2.TR1300,1VNA可用于進行諧振器Q測量。
在以這種方式測量S21S參數之后,分析數據以提取諧振器的諧振頻率和Q因子。將響應的峰值作為共振頻率,然后將兩個標記放置在比峰值低3dB的位置。峰值頻率除以峰值的3dB寬度就等于Q因子。
例如,對圖3所示電路的掃描會導致圖4所示的測量。該圖為我們提供了實驗的Q因子13.62/(13.99−13.28)=19.2。
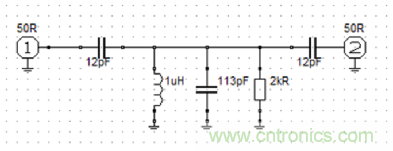
圖3
3.所示為用于VNA測量的2端口示例電路。
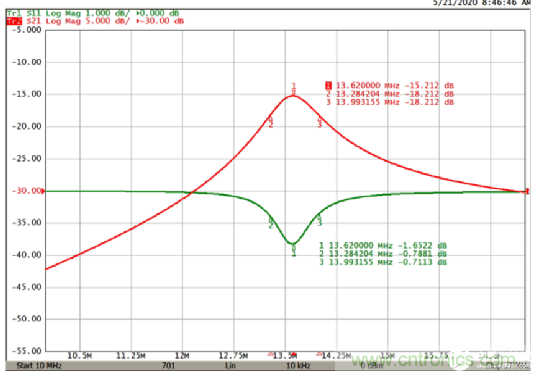
圖4
4.該圖說明了圖3所示電路的3dBQ因子測量。
忽略了12pF耦合電容器和50μl源極和負載的影響,原理圖中的近似Q系數等于113.pF電容器在13.62MHz處的導納除以電阻器的電導,或者9.673e-03/5e-04=19.3。這表明與實驗確定的值存在合理的一致性。
通過減少耦合,可以獲得更好的測量結果,使S21峰值下降至-40dB左右,從而降低負載效應。但是,S11讀數將變得很小。我們將顯示Q因子可能來自S11測量,但是數量必須足夠大才能使用。
那怎么辦呢?顯然,在S11曲線上尋找比最小值高3dB的點不是問題。上面顯示的跡線的最小值為-1.6dB,因此這顯然是不可能的。事實證明,在無損電路中。S11和S21之間存在關系:
從前面的圖中,我們可以計算出S21的值:
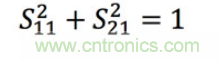
如果:
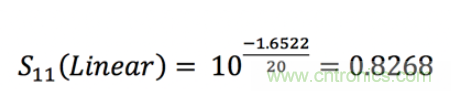
然后:
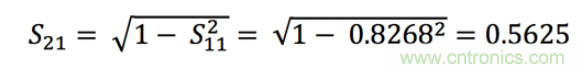
S21本身并不是真正的值,但是我們仍然可以使用它。計算S21的值(向下降低3dB)意味著乘以1/√2:
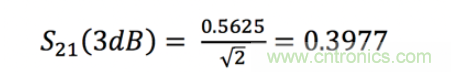
現在我們回到S11:
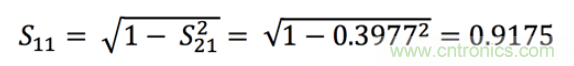
或-0.748dB。
如果我們從較早的測量結果的最小值的每一邊都找到了S11的值,則結果如圖5所示。
從所示的三個頻率,我們可以計算Q因子:
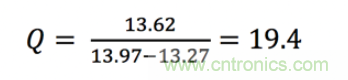
該結果非常接近于19.2的計算值。
因此,通過相對簡單的計算,就可以僅通過回波損耗測量來確定諧振器的Q因子。
(來源:電子發燒友,作者:上海韜放電子)
免責聲明:本文為轉載文章,轉載此文目的在于傳遞更多信息,版權歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權問題,請電話或者郵箱聯系小編進行侵刪。







