【導讀】作為基礎內容,先簡單介紹一下“何謂頻譜?”。根據日文版“大英百科全書 小項目版(支持電子版)”的解釋,“將電磁波分解為正弦波分量,并按波長順序排列的波譜”,將該釋義擴展開來就是“將具有復雜組成的東西分解為單純成分,并把這些成分按其特征量的大小依序排列(部分省略)”。
上一篇以“差模噪聲與共模噪聲”為題對EMC的基礎–EMC相關的術語意義進行了解說。本文將介紹“頻譜基礎”。
作為基礎內容,先簡單介紹一下“何謂頻譜?”。根據日文版“大英百科全書 小項目版(支持電子版)”的解釋,“將電磁波分解為正弦波分量,并按波長順序排列的波譜”,將該釋義擴展開來就是“將具有復雜組成的東西分解為單純成分,并把這些成分按其特征量的大小依序排列(部分省略)”。雖然所引用的解釋比較簡短,不過再次仔細思考就會覺得“的確如此”。
這里介紹的頻譜是指電氣信號的頻譜。具體來說,是基于通稱“頻譜分析儀/Spectrum Analyzer”的頻譜分析儀器的數據(橫軸作為頻率,縱軸作為功率或電壓)進行介紹。
頻譜基礎
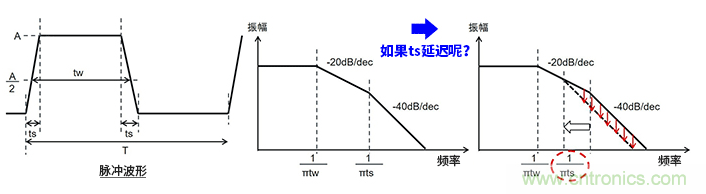
本文的主題是“開關電源的EMC”,因此電氣信號是以開關信號為前提的。首先來看下面的原理示意圖。在表示開關信號的脈沖波形中,包括tw(脈沖寬度)和ts(上升/下降時間)。
中間的圖是基于傅里葉變換的理論上的脈沖波形頻譜。這是“振幅隨著頻率的升高而衰減,衰減斜率隨著tw和ts而變化”的常見頻譜。
右圖表示脈沖的ts延遲后的頻譜變化。斜率變為-40dB/dec時的1/πts頻率降低是理所當然的,最終結果是其后的振幅減少。簡而言之就是“當ts延遲時頻譜的振幅衰減”。
接下來將使用實際的頻譜分析儀數據來看頻率等其他參數變化時的頻譜變化。這里的關鍵點是“對于信號波形的變化,頻譜將以怎樣的趨勢變化”。這是用來通過實際的開關電源電路的開關相關的頻譜來分析并解決EMC問題所必須的知識。
波形變化與頻譜變化
前面給出的圖是用來比較的默認條件下的數據。下面波形圖中的條件是:振幅10V,頻率400kHz,Duty(占空比)50%,tr/tf(上升時間/下降時間)10ns。
中間的圖表示n次諧波和振幅(V)的關系。1倍的頻率=基波,也就是說400kHz的分量最大,以奇數倍的頻率形成頻譜。
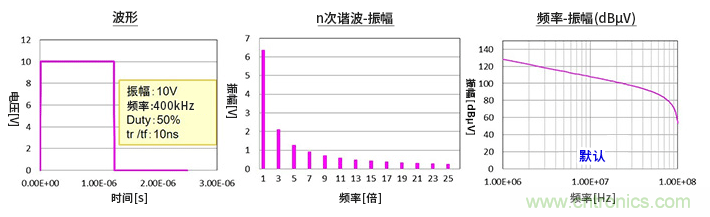
諧波僅為奇數次是Duty為50%=1:1的頻譜特征。各分量的大小為基波分量的1/次數,例如3次諧波分量為1/3,n次諧波分量為1/n。
右圖是振幅為dBµV的對數曲線圖。順便提一下,dBμV是基于以1µV電壓為基準的電壓比的dB值。
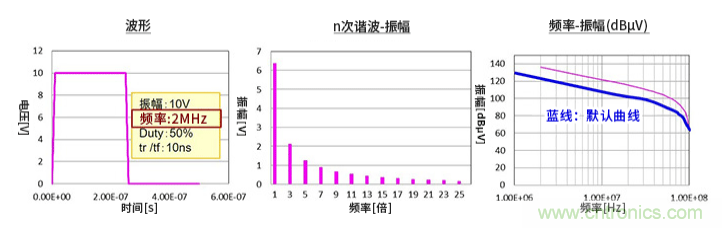
①將頻率變更為2MHz時的頻譜。從頻率-振幅(dBµV)關系圖可以明確看出,當頻率增加時振幅整體增加。
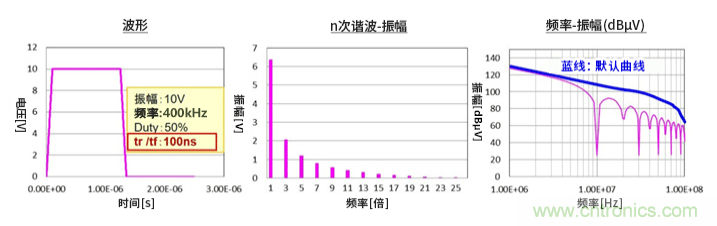
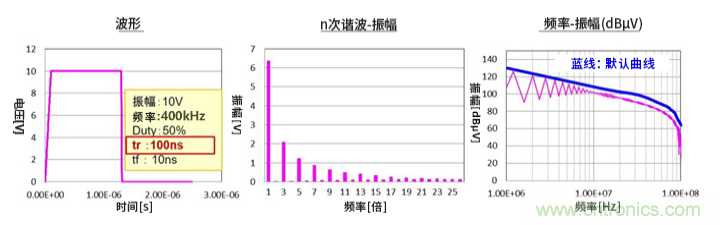
②tr和tf同時延遲為100ns時的頻譜。結果如原理示意圖所示,進入-40dB/dec衰減時的頻率降低,頻譜的振幅衰減。
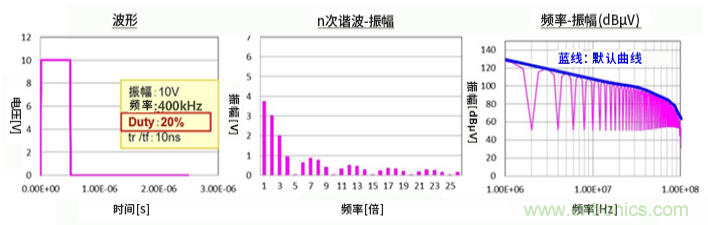
③將Duty50%變為20%時的頻譜。由于Duty不是1:1,因此會產生偶次諧波,但峰值基本上沒變化。隨著脈沖寬度tw變窄,基波頻譜的振幅衰減。
④僅tr(上升時間)延遲時的頻普。tr相關的分量因tr延遲而從更低的頻率開始衰減。
下面匯總了每種情況的結果。總而言之,當頻率較低且上升/下降較慢時,頻譜會衰減。從EMC的角度來看,也就是頻譜的振幅較低時更有利。

另外,這里的“頻譜”是指英語的“Spectrum”。雖然這并非本文主題,但稍微介紹一下僅作為了解。
(來源:ROHM,作者:ROHM)
免責聲明:本文為轉載文章,轉載此文目的在于傳遞更多信息,版權歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權問題,請電話或者郵箱聯系小編進行侵刪。








