【導讀】“科學家阿瑟·阿什金利用一束高度匯聚的激光形成三維勢阱來捕獲、操縱極其微小的粒子,利用激光將小粒子推向光束中心,并將它們限制在那里,從而更好地操縱。光鑷能夠抓取分子,把它們移動到想要的地方,并對它們展開操作”。光鑷背后的物理,及引申出的深刻電磁理論,值得梳理和探討。
移動物體需要力。眾所周知,速度隨時間變化產生加速度;因而動量隨時間變化,產生力。電磁系統也有力,比如電場力qE,磁場力qv x B。產生這些力對應的動量叫機械動量。但是,該機械動量并不是守恒量,一如電子-電磁耦合系統中電子的動量也不是守恒量一樣。
如果把電磁場或光看成粒子,一如一顆顆子彈,它也能傳遞力至物體上。當電磁場經歷鏡面反射的時候,因為速度方向的改變,必然將動量傳遞給鏡面,產生試圖移動鏡面的力。如果一束光被物體吸收,也有動量傳遞給該物體。如果物體足夠小,足夠輕,這種力是有可能移動物體的。這種場產生的動量,應該和電磁場的粒子性有某種聯系。根據德布羅意假說,動量p = ?k = ?ω/c = E/c。如果把能量寫成功率和時間微分的乘積,功率寫成能流密度E x H和面積微元dS的乘積,時間寫成距離微元dl比上光速c,最終得到場動量密度表達式E x H / c2。而場動量加上機械動量是一個守恒量,它們共同產生的力,可用麥克斯韋應力張量來計算。這也是光力中最常用的計算方法。
如果進一步深入分析場動量的表達式,將會變得很有趣。在這個表達式中,如果將電場分解成縱向分量(近場、有源區)和橫向分量(遠場、無源區),縱向分量對應的項,∫v El x H / c2 dV,化簡后居然是量子力學中對應的場動量qA。該場動量qA和電子動量mv加在一起是守恒量,被量子化后即正則動量算子。而剩下的橫向分量,∫v Et x H / c2 dV,繼續分解,又可以分成兩項,一項是自旋動量,另一項是軌道動量。前者和電磁波的極化有關,圓極化帶有自旋角動量。后者和電磁波的波前有關,渦旋電磁波(如高斯拉蓋爾波束)帶有軌道角動量。帶有自旋角動量和軌道角動量的電磁波可以產生力矩,旋轉粒子。電磁場中的自旋和軌道角動量的表達式和電子系統驚人的一致,除了自旋算子變成了3x3的Pauli矩陣而已。軌道動量密度和軌道角動量密度表達式正比于?E | -i?∇ | E? 和?E | r x (-i?∇) | E?,這顯然符合角動量算子的形式,L=r x p= r x (-i?∇)。
如果把軌道角動量空域表達式做傅里葉變換,得到k域表達式,k域的軌道動量密度不是別的,正是Berry Connection的定義。將Berry Connection沿著某閉合路徑積分得到Berry Phase,除以2π就得到陳數。對圓極化的渦旋電磁波,該陳數聯系到電磁波的自旋(σ = -1,1)和軌道(l = 1,-1,2,-2,…)拓撲電荷數之和。盡管渦旋波在自由空間通訊中遭遇模式串擾、波束發散、多徑效應的困擾,它仍然是一個很穩定的波束,小的擾動不會改變其拓撲性質。而理解渦旋電磁波和拓撲絕緣體之間的聯系,及軌道角動量通訊中如何挖掘渦旋電磁波的拓撲性質,是值得深入探索的課題。而從物理角度具有拓撲穩定的渦旋電磁波,在通訊工程上的實際應用仍需極大努力。“Even though many problems are a ‘done deal’ in the physics community, they are not a ‘done deal’ in an engineering community. Much blood, sweat, and tears are needed.”
上述觀點,是作者個人的思考和體會,并不代表正確嚴格的電磁理論。歡迎大家批評指正!本文的數學公式(未發表),見如下圖片。
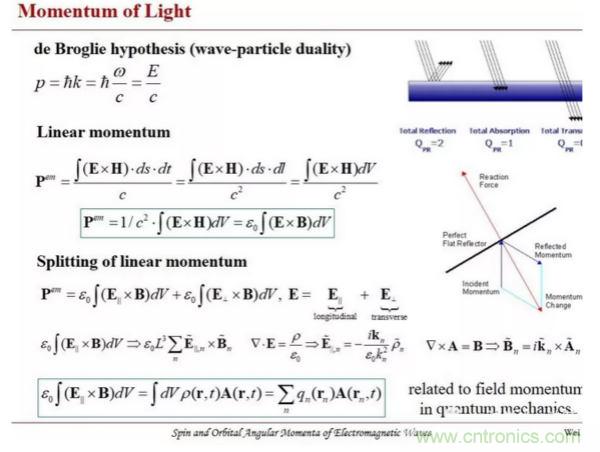



本文轉載自 電磁兼容EMC。
推薦閱讀:
在功耗敏感型應用中利用高效率 超低功耗開關穩壓器為精密SAR ADC供電







