中心議題:
- 提出運用在PLL基礎上對LC諧振頻率進行測試的原理
解決方案:
- 一種快速,高精度和不受溫度變化影響的測試LC諧振頻率的原理
研究背景
傳統上LC諧振頻率的測試方法是通過逐點改變加在 (直接或者間接 )LC諧振回路上信號頻率來找到最大輸出時的頻率點,并把這一頻率點定義為 LC諧振頻率。很明顯這種測試方法的缺點是:測試方法比較復雜,測試時間長,測試精度低,而且直接受到諧振體尤其含磁芯諧振體由于較長測試時間所引起溫度變化的影響。本論文中所要介紹的應用在PLL基礎上對LC諧振頻率進行測試的原理和方法具有快速,高精度和不受溫度變化的影響,并且還具有測試方法簡單的特點。本論文主要從理論上簡明使用PLL對LC諧振頻率進行測試的原理。
基本原理
測試LC諧振頻率可以通過圖1所示的2次耦合回路形式來完成。其中 L2C2組成一個待測LC諧振回路, L1是發射線圈,Li是只有單匝的接受線圈。一般測試時可以滿足: 1/ωCi》Ri》ω Li,M2》M1》M3的測試條件。這里ω是實際工作角頻率,Ri,Ci與 R1,C1分別是接受線圈與發射線圈的接入回路的電路參數, M2是待測LC諧振回路與接受線圈間的耦合系數,M1是待測LC諧振回路與發射線圈間的耦合系數,M3是發射線圈與接受線圈間的耦合系數。滿足上述測試條件下從圖1可以得出。
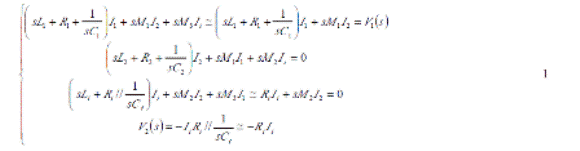
這里V1是發射信號的電壓, V2是接受信號的電壓,則測試回路的傳輸函數是由下式所決定的。
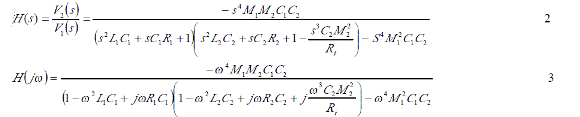
圖1LC諧振測試回路的原理圖
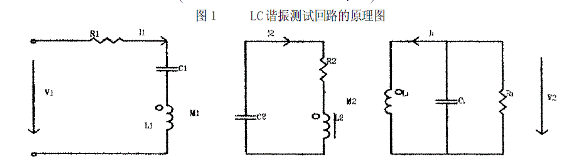
根據LC諧振回路的性質可以得到:
![]()
這里ω 01與ω 02(ω02》ω01)分別是由發射線圈 LC諧振回路與待測 LC諧振回路的諧振角頻率,實際應用時 Q2在100左右,而 Q1小于1。此時式3可簡化為:
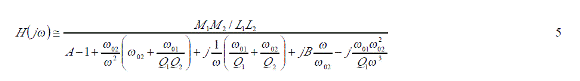
所構成。其中:
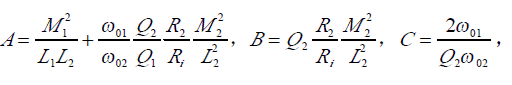
如果實際工作角頻率與待測諧振角頻率間的角頻率差 Δω控制在遠小于 ω02,這樣可以無視 Δω的高次項,式5可以作進一步簡化。
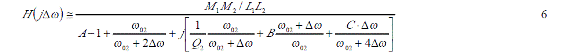
所以振幅函數和相位函數可以分別簡化為下式。
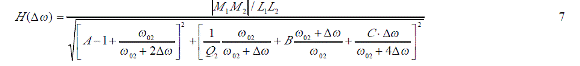
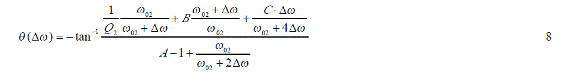
諧振時振幅為最大,此時振幅和相位函數可以分別由下式給出。
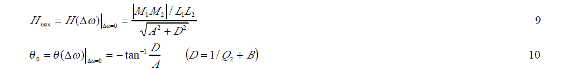
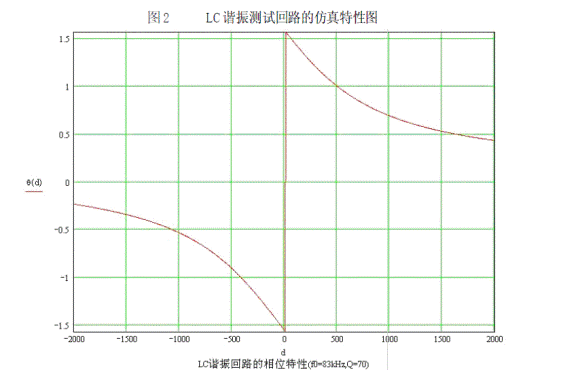
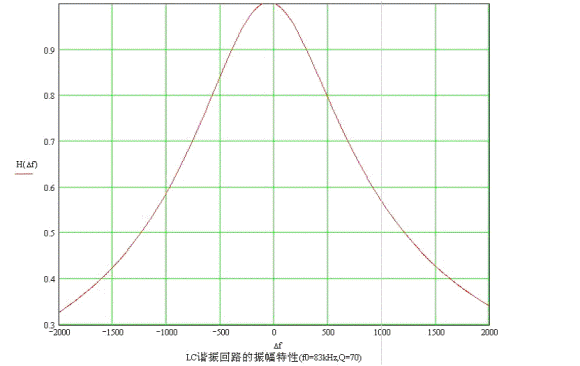
設定電路參數為f02=83kHz、f01=800Hz、Q1=0.1、Q2=70、M2/L2=0.2、M1/L1=0.1、M1/L2=10-4、R 2/Ri=10-3時在Mathcad下仿真結果如圖 2所示,其中振幅特性是歸一化后的特性, d=Δf。從圖中可以看出有跳周現象,這是由于式 8分式中分母部分發生歸零引起的。該點角頻率差定義為 Δω0,則由式 8可以得出以下關系式。
![]()
上式滿足了PLL工作條件,即使用上記相位信號的 PLL回路最終鎖定在待測 LC回路的諧振頻率上。實際使用中根據測試條件很容易達到 A、B《1,由圖1所組成的回路感度是由:
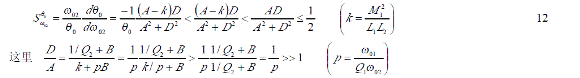
所決定的[2]。所以即使ω02有相當大的變化θ 0的變化也是很小的,即 θ0可以看作為常數。以下我們僅討論 PLL動作范圍在諧振角頻率附近時的工作情況,有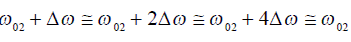 。則式8作以下變更。
。則式8作以下變更。
![]()
使用式10對相位進行補償,經過補償后式8的實際相位Δθ是:
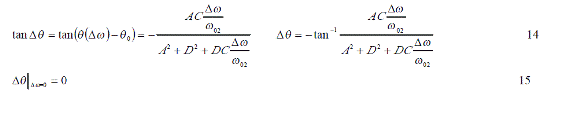
補償方法一般可以使用雙向延遲回路。由于實際應用時是使用固定延遲回路的,測量到諧振角頻率與真實諧振角頻率間會產生一個誤差,假設這個諧振角頻率差為Δω02,并且工作角頻率范圍滿足Δω《ω 02。假設真實所需補償的相位是由式10所決定的,則與固定相位補償會產生一個相位差 Δθ0,則有式 10可以得到以下關系式。
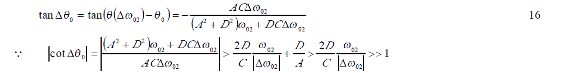
這里Δω 02是當PLL回路工作在鎖定狀態下由于固定延遲所產生的諧振角頻率差,對于一個具體的 LC諧振回路這是一個常數。當測試條件滿足時,即使引進固定相位進行補償其產生的誤差也是很小的,幾乎可以忽略不計。
實例
根據本文中所推出的原理試作了LC諧振頻率測試機分別對6個種類LC諧振體樣本(產品)進行測試。本LC諧振測試機已應用在6個種類LC諧振體的生產和產品檢驗上。具體結果參照表1和表 2。
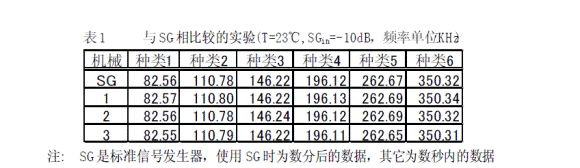

.結論
本論文提出了一種快速,高精度和不受溫度變化影響的測試LC諧振頻率的原理,并通過具體實例驗證了上述原理的有效性,作為今后一種研究的課題是如何解明針對發射和接受端為相同頻率狀態下 PLL工作特征與發射和接受端為不同頻率狀態下 PLL工作特征的差異性。
參考資料
[1]「高頻電路」上清華大學通信教研組1979年第一版人民郵電出版社
[2]「模擬集成回路設計技術」上 P.R.格雷/R.G.邁耶共著永田穣監譯 1990年版倍風館
作者介紹
1982,2-1987,1上海交通大學夜大學電子工程系畢業
1992,4-1994,3日本電氣通信大學大學院電子情報專業碩士、
長期從事于產品設計開發工作,對于各種數字和低高頻模擬應用電路,從理論推證到具體開發設計具有豐富的理論知識和實踐工作經驗,尤其精通于鎖相環電路的設計,并且在理論上有自己獨到的見解。
去焊接工藝與測試社區看看








