【導讀】本文旨在探討如何用組合器件一類的加速度計提高傾角測量的精度。在乘用車上,電動駐車制動器(EPB)被用于使汽車在平坦的分級道路上保持靜止。這是通過用一個單軸或雙軸加速度計測量傾角來實現的。一般做法是將一個X軸/Y軸或Z軸低g加速度計裝在EPB控制單元中一個專門的模塊中。
現在,越來越多的汽車配有ESC(電子穩定控制)功能,在單個芯片中集成了組合式低g加速度計和陀螺儀。這樣做是為了防止汽車側滑和翻車;如今,ESC功能已經成為世界各國或地區法律的強制要求。如果通過組合器件(單芯片、組合式加速度計和陀螺儀)實現傾角測量,則不必在車上安裝一個獨立的EPB模塊,結果可以大幅降低汽車的成本。由于組合器件通常用于ESC,所以并未針對傾角檢測優化,并且通過組合器件測量傾角時,測量精度有時無法達到要求。由于組合器件是XY軸或XYZ軸,所以通常用X軸進行傾角測量,EPB模塊中的部分傳統型低-g加速度計使用的是Z軸,因為它是垂直安裝在發動機艙里的。檢測軸應該與重力垂直,才能取得更高的精度——我們稍后會討論這一點。
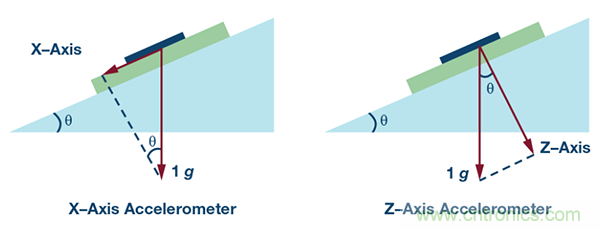
圖1. X軸和Z軸加速度計的安裝示意圖。
對于汽車中的傾角測量,評估精度是非常重要的。不妨想像,您的車停在絕對平坦的地面,因此,加速度計計算的傾角應該是0°。如果您的車停在斜坡上,就應該精確地檢測出傾角,以便正確地激活剎車系統。
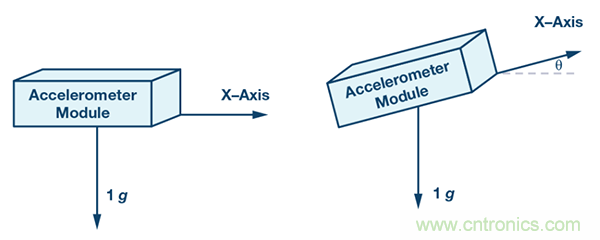
圖2. X軸檢測傾角測量示意圖。
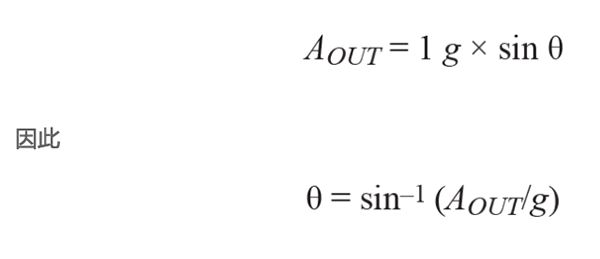
其中:
AOUT 為加速度計的輸出,單位為g。
θ 為斜坡的傾角,單位為度。
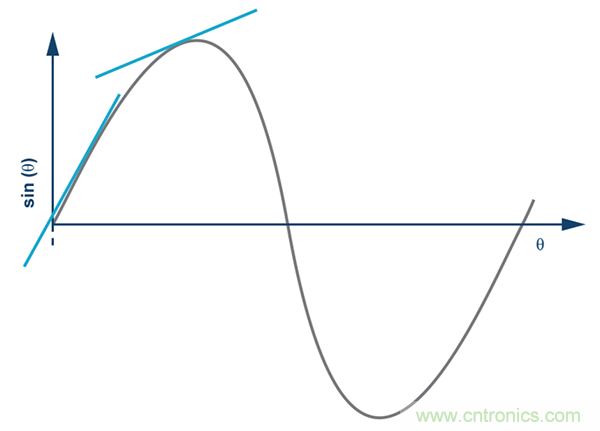
圖3. sin θ對θ隨θ增大而下降的靈敏度。
由于sin θ是一個非線性函數,所以,AOUT與θ之間的關系是非線性 的,在接近零時其線性度處于最佳狀態,即其此時具有最佳的測量精度。隨著θ的增大,測量精度下降。這正是檢測軸應與重力垂直的原因,因為道路坡度將接近零
對于汽車傾角測量,不必在全斜坡坡度的條件下考慮系統。現實世界中,道路上的絕大多數斜坡坡度不會超過30°。我們只需要分析在±30°的范圍內分析貢獻因素的精度即可。
影響系統級測量精度的貢獻因素有多個:
* 靈敏度誤差和初始絕對失調
* 非線性度
* 與初始絕對失調的總失調變化
* 噪聲
靈敏度誤差和初始絕對失調
靈敏度誤差
靈敏度是對輸入-輸出測得的傳遞函數的斜率,通常為+1g和–1g。靈敏度誤差為器件間的靈敏度偏差。例如,有些加速度計的最大靈敏度為3%。
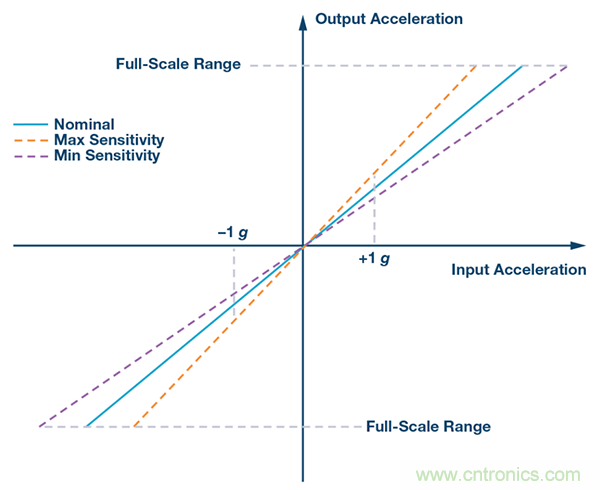
圖4. 輸入-輸出加速度靈敏度誤差。
初始絕對失調
范圍內的失調約為25°C;例如,在模塊制造完成后立即測量的值為25°C ± 5°C。初始絕對失調表示大量器件的實測偏移值的標準差。
兩點校準
對于傾角測量應用,兩個主要的誤差來自失調誤差和靈敏度誤差。這兩種誤差會導致不可接受的檢測結果,因此不得忽略。如果我們希望消除這些部分誤差,則應對加速度輸出進行校準。一般地,要對傾角測量的失調和靈敏度進行一次校準。若要考慮失調和靈敏度誤差,則加速度計輸入與輸出的關系為:
其中:
- A輸出 為失調誤差,單位為g。
- 增益為加速度計的增益,理想值為1。
- A實際為施加于加速度計的實際加速度,單位為g。
有兩種基本校準技術;其中一種是單點校準。這種校準的具體做法是在加速度計上施加一個0g場,然后測量輸出。這類校準只能用于校準失調誤差,不能校準增益誤差。然后,從實際輸出值中減去0g場里的輸出結果,消除失調誤差。這種校準方法非常簡單,但精度不足,因為仍然存在靈敏度誤差。另一種方法是1g翻轉校準,在+1g和–1g時采用兩點校準,并在每個+1g和–1g場內按照以下公式測量加速度輸出:
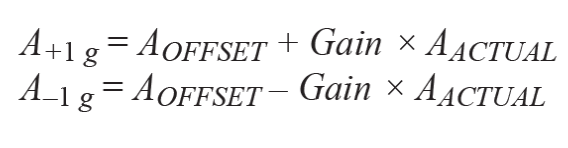
其中,失調A失調的單位為g。
以這兩點信息為基礎,可以按照以下方法解出失調和增益:
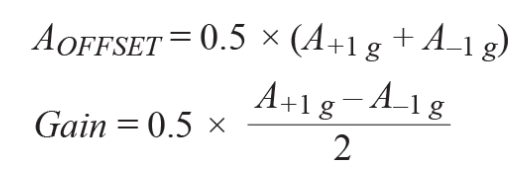
其中,+1g和 1g測量值、A+1g和A–1g均以g為單位。
經過這一次校準以后,可以用該等式計算實際加速度,每次都會消除失調誤差和靈敏度誤差。
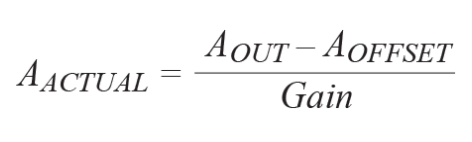
其中,A失調和A輸出以g為單位。
非線性度
器件的非線性度為測得加速度(AMEA)與理想線性輸出加速度(AFIT)之間的最大偏差。加速度測量數據集應包括加速度計的滿量程范圍。其測量方式為Max(|AMEA – AFIT|)。
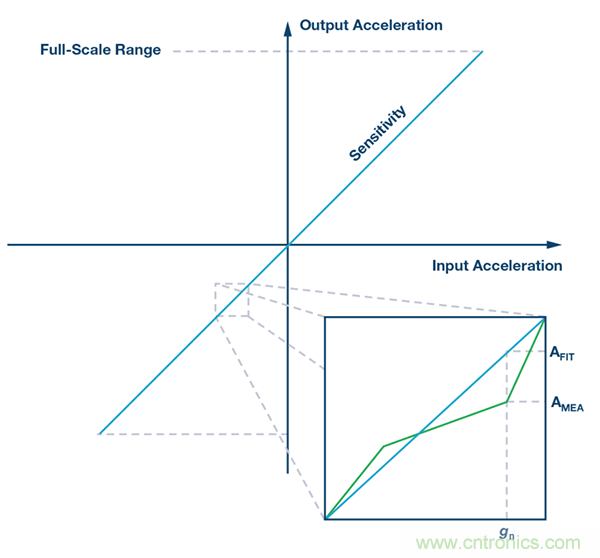
圖5. 器件非線性度。
其中:
AMEA為給定gn下的測得加速度。
AFIT 為給定gn下的預測加速度。
多數加速度計或組合器件在給定輸入加速度計范圍內均存在非線性——例如,30 mg ± 2g的范圍。對于傾角測量應用,輸入坡道斜率在±30°以內,這意味著輸出加速度范圍在±500 mg (±1g× sin 30°)以內,所以應重新評估該范圍內的非線性度。由于非線性度在整個輸入范圍內是非線性的,所以,很難準確地量化評估這部分誤差。然而,由于該器件的數據手冊通常都很保守,線性度為30 mg,輸入范圍為±2g,用10 mg計算±500 mg范圍內的誤差更合理些。
與初始絕對失調的總失調變化
與初始絕對失調的總失調變化為溫度、應力和老化效應導致的失調的最大偏差。該偏差是相對于給定器件的初始絕對失調進行測量的。這是精度總誤差的主要貢獻因素。
在溫度、應力、老化等所有這些因素中,變化與溫度在總失調變化中占比很大。一般地,變化與溫度曲線是二階曲線,通常為旋轉拋物線。為了消除這部分誤差,可以在系統級執行三點校準。對于給定器件,可按下列步驟校準輸出失調隨溫度的變化值。
第1步:
使器件的輸出響應以某個 ?N0值偏移。溫度校準流程的第一步是 消除環境溫度下的失調。
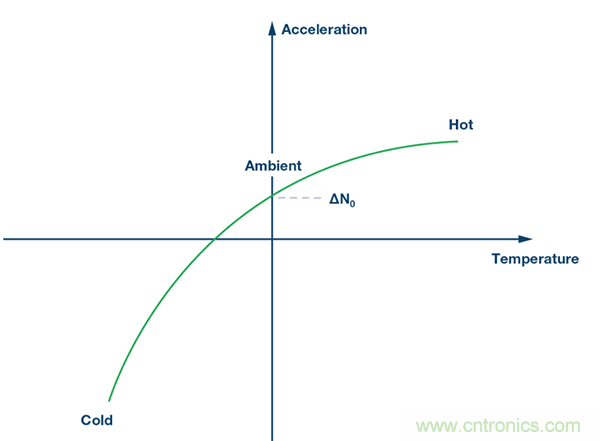
圖6. 第1步:消除環境溫度下的失調。
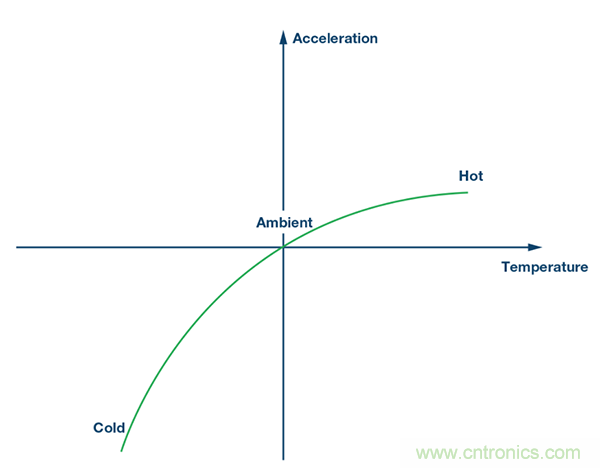
圖7. 第2步:在消除環境溫度下的失調之后。
第2步:
接下來,在高溫下測試器件,用獲得的新信息生成失調校正線性公式。
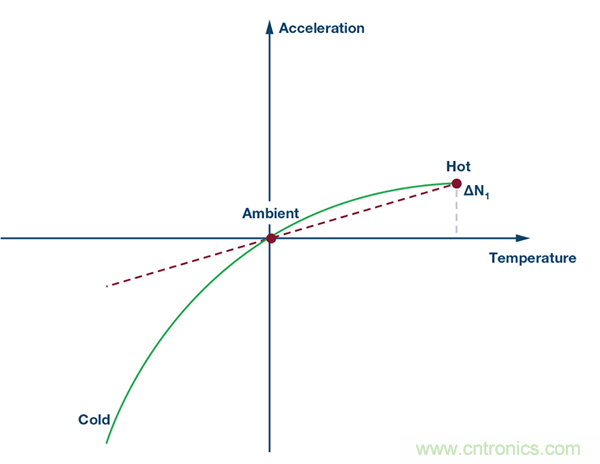
圖8. 第3步:消除高溫下的拋物線旋轉分量。
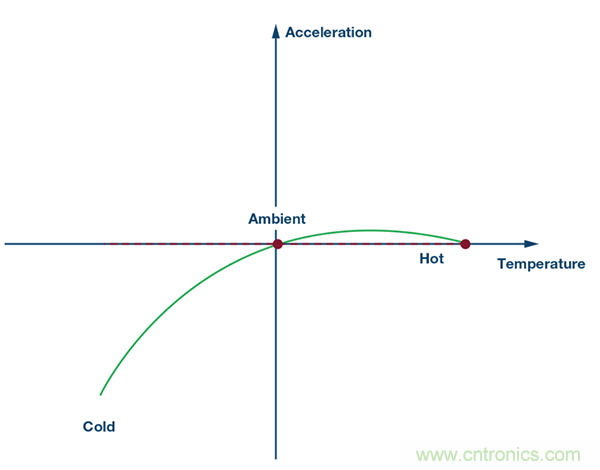
圖9. 第4步:在消除高溫下的拋物線旋轉分量之后。
第3步:
給現有公式添加一個二階分量,校正失調剩余部分。設二階曲線遵循以下公式:
這是二階拋物線公式,已經通過第1步和第2步消除了旋轉分量。
在該公式中,該二階拋物線有三個解:
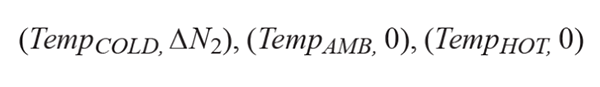
然后,我們可以得到溫度系數 a, b, c.
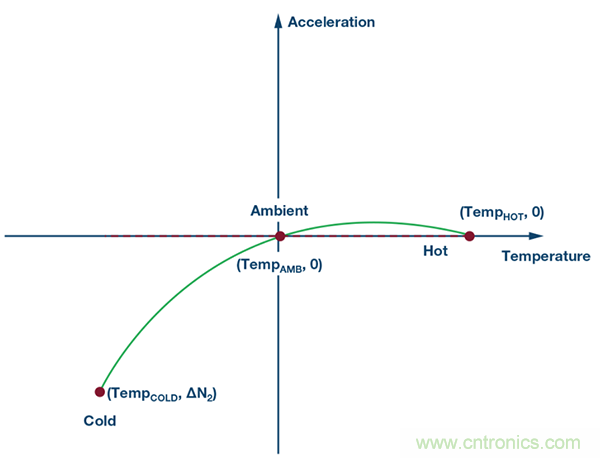
圖10. 第5步:添加二階分量,消除剩余失調。
有關?N0, ?N1, ?N2, a, b, c 的所有溫度系數信息應該存儲在系統非易失性存儲器中,同時需要一個板載溫度傳感器。系統會在每次上電后例行校準加速度計,確保消除失調隨溫度的變化值。
噪聲
基于單個數據樣本測量傾角不一定可靠。即使加速度計的噪聲為零,傾角測量也是在汽車啟動時測量的,所以,需要減小發動機、過往車輛或乘客在車上來回移動導致的任何振動。最好的辦法是在不降至最低數據速率要求的條件下,在盡量長的時間內做數據平均。數據平均算法會減少rms噪聲。
假如我們對噪聲采樣,結果可得到每個樣本的方差
求一個隨機變量的均值,獲得以下方差,
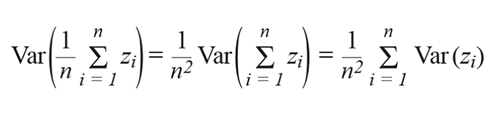
由于噪聲方差保持于σ2不變,
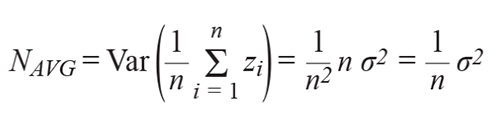
以上推導顯示,對同一未校正噪聲的n次實現求均值可使噪聲功率減少n倍,并使rms噪聲減少√n。
由于隨機噪聲受高斯分布影響,所以,rms噪聲等于高斯分布的標準差。6σ以內的最小分布為97%。
例如,如果以1 kSPS的采樣率對每100 ms的數據求均值,則最大rms噪聲 = 0.4 mg,即是說如果以6σ作為與平均值的距離,則此時的峰值噪聲僅為2.4 mg。
用于與rms值相乘的因數取決于器件要執行的任務的統計需求。例如,如果選擇6作為因數(峰峰值噪聲為6 × RMS_Noise),則算法在器件生命周期內要運行的次數會影響超過最差情況6 × RMS_Noise 的概率。可總結如下:
E為在生命周期內超過最差情況的預期次數,M為生命周期內的運行次數,r為超過最差情況的概率。基于此,我們可以通過乘以rms噪聲評估出一個合理的因數。
小結
以ADI公司的ADXC1500/ADXC1501(組合式陀螺儀和2軸/3軸加速度 計)為例,所有誤差貢獻項均列于表1中,包括校準和不校準兩種情況。我們可以假設,總失調變化為二次曲線,并且其在溫度范圍內的變化占總失調變化的80%。另外,以6為因數乘以最大rms噪聲。
一個陀螺儀和一個三軸加速度計的單芯片集成方案可以實現多種新型應用,尤其是在汽車安全系統和工業自動化應用領域。為了設計更加可靠、高精度的汽車安全系統,例如,穩定的電子控制系統(ESC)和側翻檢測系統,盡量減少系統誤差至關重要。汽車中已安裝這些傳統型底盤控制系統,包括防抱死制動系統、牽引控制和偏航控制系統。
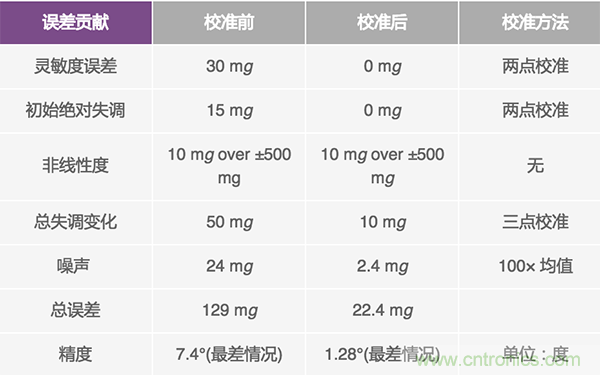
表1. 校準前后的誤差貢獻
推薦閱讀:









