【導讀】很多工業裝置都會出現斷路器頻繁誤跳閘的現象,隨機且偶然,跳閘原因讓人摸不著頭腦。為何斷路器會出現頻繁誤跳閘的現象?幕后的黑手到底是誰?謎底就是過流!
為了找出造成故障的原因,我們用電流鉗表對設備電流進行測量,然而發現幾個鉗表所測電流值相差非常大,例如下圖的現場測試圖所示。那么哪個值才是正確的呢?圖2是該電流的波形。
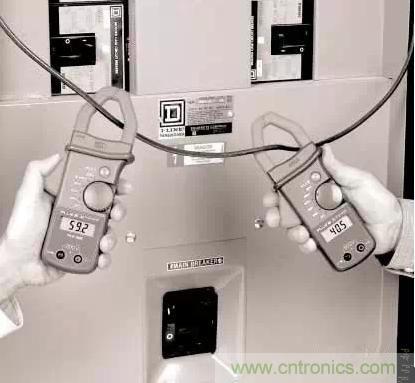
圖1 左邊電流為5.92A,右邊電流為4.05A
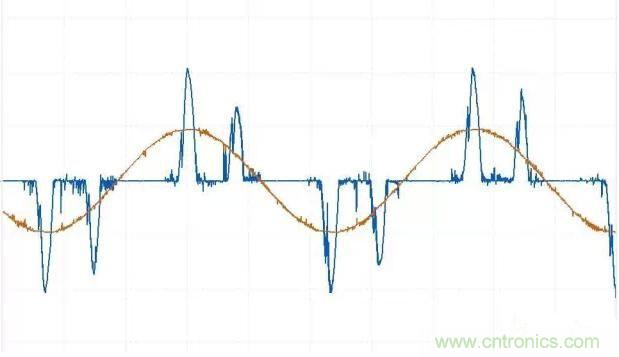
圖2 對應的電流波形
從電流波形可以看出,該負載是一個非線性負載,波形不是標準的正弦波,圖1中左邊的電流表是真有效值測量儀,右邊的是按有效值校準的平均值測量儀。那么為什么這兩種電流表測出來的電流值會相差那么大呢?在很好的理解它們差異所在之前必須首先了解有效值的確切含義。
什么是有效值(方均根值)?
交流電流的有效值(RMS)等于在同一電阻性負載回路中,與其產生等熱量的直流電流的大小。使用交流電時,電阻產生的熱量與一個周波內的平均電流的平方成正比。換而言之,產生的熱量和電流平方的平均值成正比,也就是說電流值和這個平方的平均值開方后的值也就是有效值成正比。(由于平方后總是正數,所以不用考慮極性問題)
對于如圖 2 所示的純正弦波,有效值是峰值的 0.707 倍(或者說峰值是有效值的 即 1.414 倍)。換句話說,有效值為 1 安培的純正弦波電流的峰值電流為 1.414 安培。如果波形值僅僅被簡單的平均(對半個負波形取反),平均值就是峰值的 0.636 倍,或是有效值的 0.9 倍。圖 3 所示為這兩個重要的比例關系。
波頂因數=峰值/有效值=1.414
波形因數=有效值/平均值=1.111
[page]
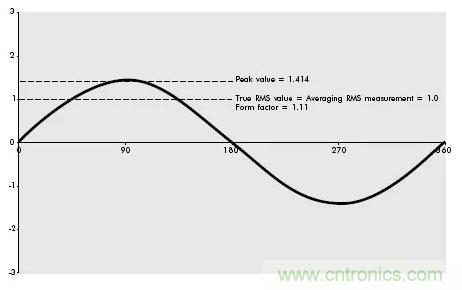
圖3 純正弦波
在測量一個純正弦波(僅限于純正弦波)時,簡單的測出平均值(0.636 倍峰值),再乘以波形因數 1.111(即 0.707 倍峰值)所得到的數值是完全正確的,這個數值也被稱為有效值。這種方法被廣泛用于所有的模擬測量儀(此時平均值是靠線圈運動的慣性和阻尼作用來實現的)和所有舊式、儀表和大多數電流表數字萬用表上。這種技術被稱為“平均讀數,按有效值校準”的測量方法。 問題是這種測量方法只適用于純正弦波,而在現實的電氣裝置中根本不存在純正弦波。圖 4 所示的波形圖是一個接入個人電腦后所產生的典型電流波形圖。方均根值仍然是 1 安培,但是峰值要明顯高于純正弦波時的峰值,為 2.6 安培。
同時平均值則小得多,為 0.55 安培。
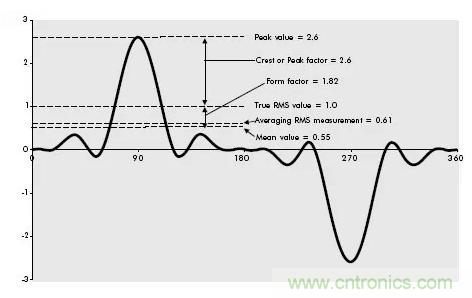
圖4 個人計算機的典型電流波形圖
如果這個波形用“平均讀數,按有效值校準”的測量儀進行測量,它的讀數為 0.61 安培,比真有效值(1 安培)少了將近 40%。
至此,也就不難理解為什么斷路器在“不滿載”狀態下會出現故障和頻繁誤跳閘啦。所以,針對非線性負載的信號測量,需要選擇“真有效值“表進行測量,才能正確評估實際電流,從而正確選擇合適的導線。
功率分析儀提供精確的真有效值測量,圖5是功率分析儀的測量原理圖。
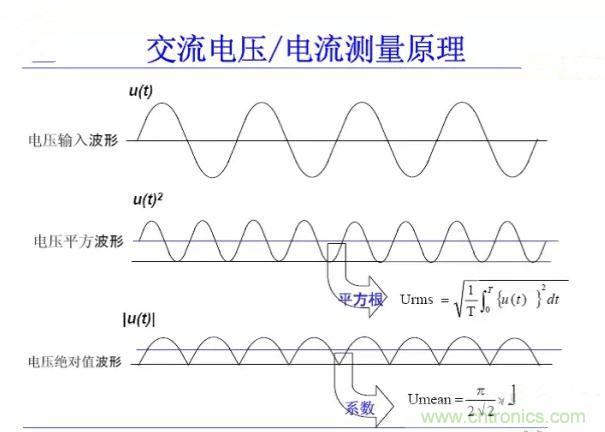
圖5 功率分析儀測量原理
隨著電力電子的快速發展,開關技術得以廣泛應用,同時碳化硅技術的發展讓更高的開關頻率得以實現以滿足更高效率的電源設計。PA系列功率分析儀帶寬高達5MHz,采樣率高達2MS/s,滿足未來高頻的測量需求。
相關閱讀:
E9D漏電保護斷路器 檢測不容忽視的30mA
針對斷路器失靈保護問題的分析
設計中有關熔斷器和斷路器的選型方案








