中心議題:
- 熱應力理論模型和物理模型
- LED瞬態溫度場分布實驗、仿真結果與分析
解決方案:
- LED 瞬態溫度測試實驗與仿真
- LED 熱應力與熱變形的模擬結果與分析
- 基板路徑上的熱應力、應變及剪應力的模擬與分析
- 材料導熱系數對應力,應變和溫度的影響分析
本文以熱應力理論為依據,模擬了LED 瞬態溫度場和應力場分布的變化,并與實測的LED 基板底部中心溫度變化情況進行了對比研究;并分析了瞬態溫度場和應力場的對應變化關系;模擬研究了鍵合層材料導熱系數對LED 結溫和最大等效應力的影響;計算了基板頂面平行于X 軸路徑上熱應力、應變及剪應力的變化趨勢。
1 熱應力理論模型及物理模型
根據傳熱理論,具有內熱源的大功率LED 瞬態溫度場分布應該滿足如下方程:

其中:T 為溫度;t 為時間;x, y, z 空間三維坐標系;α 為熱膨脹系數,α 滿足方程:

其中:λ 為導熱系數,ρ 為密度,c 為比熱容。按照熱彈性力學理論,LED 溫度梯度導致的熱膨脹受到外部約束時產生的瞬態熱應力,滿足如下方程:

式中:σ 為熱應力,α 為熱膨脹系數,E 為彈性模量,T 為溫度,Tref 為參考溫度。由式(3)可以看出,LED 內部溫度場是確定熱應力大小的前提,而溫度分布由熱傳導微分方程(1)決定,只要給出相應的邊界條件即可得到溫度場及應力場分布。
以Lumileds 的1 W 功率型LED 器件(如圖1)為研究對象,該LED 由透鏡、芯片、鍵合層、熱沉、基板及塑封料組成。熱量由芯片經鍵合層傳導到熱沉,最后由基板與空氣進行對流散熱。LED 各種封裝材料熱性能參數如表1 所示。
圖1 Lumidleds 1 W LED 模型
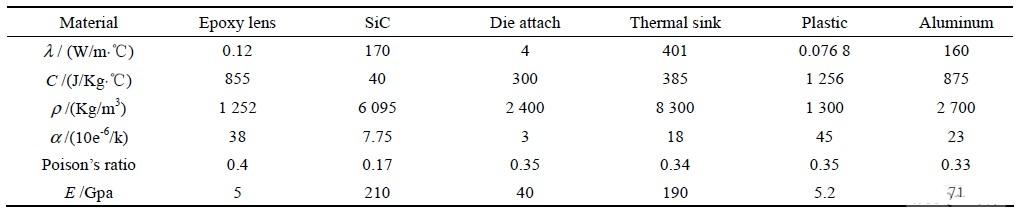
表1 LED 封裝材料的熱力學參數
[page]
2 實驗、仿真結果與分析
采用自由網格建立LED 有限元模型,熱源和鍵合層采用一級網格,其余采用六級網格。芯片輸入熱功率按90%計算為0.9 W,環境溫度為25℃,生熱率4.0×109 W/m3,在LED 模型與空氣接觸面加載對流系數為10 W/m2.℃,并忽略各層材料中的接觸熱阻,設定求解時間為600 s,時間子步為20 s,利用有限元軟件ANSYS 求解式(1)~(3)即可得到Lumidleds 1 W LED 瞬態溫度場分布。
2.1 LED 瞬態溫度測試實驗與仿真
為了驗證有限元仿真的可靠性,設計了一組實驗對Lumidleds 1 W LED 進行溫度測試,測點為鋁基板底面中心,給定電流350 mA,電壓3 V,溫度測試時間為10 min,每隔10 s 記錄一次數據,實驗結果表明點亮8 min 后,LED 基本處于熱平衡狀態,此時基板中心溫度為56℃。仿真結果表明此時LED 結溫為76.1℃(如圖2 所示)。
LED 從開始工作到穩態過程中,基板測點溫度變化曲線和仿真結果如圖3 所示,升溫過程中,實測結果略低于仿真結果,到達穩態后,兩則相差2.9℃,驗證了有限元分析的可靠性。材料參數的誤差、仿真過程中忽略了熱輻射以及將對流作為簡單邊界條件施加是產生誤差的主要原因。
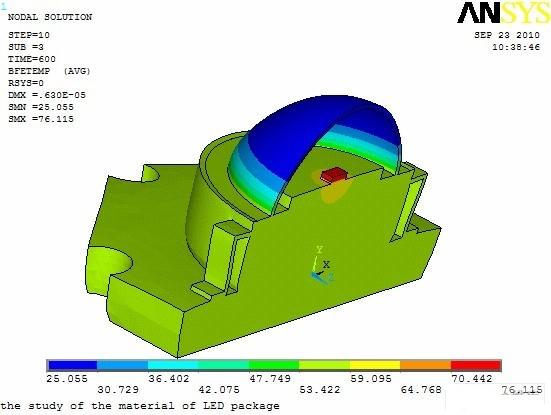
圖2 Lumileds 1 W LED 穩態溫度場分布云圖
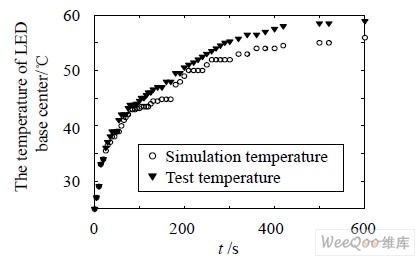
圖3 Lumileds 1W LED 基板中心點溫度實測數據與仿真數據對比
2.2 LED 熱應力與熱變形的模擬結果與分析
在計算得到瞬態溫度場分布后,將熱單元solid70 轉換為結構單元,用循環命令將每一個時間步的溫度場讀入到應力場,并在基板底面三個方向加約束,計算得到穩態時應變和應力場如圖4(a)、(b)。
圖4(a)是Lumileds 1 W LED 在最終時刻(600 s)后總位移云圖,內部帶網格云圖表示未變形前的結構,另一個實體云圖表示LED 在受熱膨脹后的變形效果,這里對變形量按比例進行了放大。由圖可見,熱變形主要集中在透鏡和塑封料處,特別是透鏡與塑封料接觸地方,最大變形量達到6.3 μm。由于基板底部加了X、Y、Z 三個方向約束,相當于基板底部被固定,因此基板底部位移量為0 μm。
圖4(b)是LED 在穩態時應力分布云圖。由圖可見,透鏡、外封塑料層和基板頂部的熱應力很小,基板底部應力明顯大于頂部。這是由于基板底部熱膨脹受到X、Y、Z 三個方向的約束所致。圖5(a)為基板底部的應力分布圖,最大在基板底面的邊角處,為163 MPa;圖5(b)顯示基板頂部最大的熱應力在熱沉與基板交界處,基板頂部邊角處只有1.43 MPa。
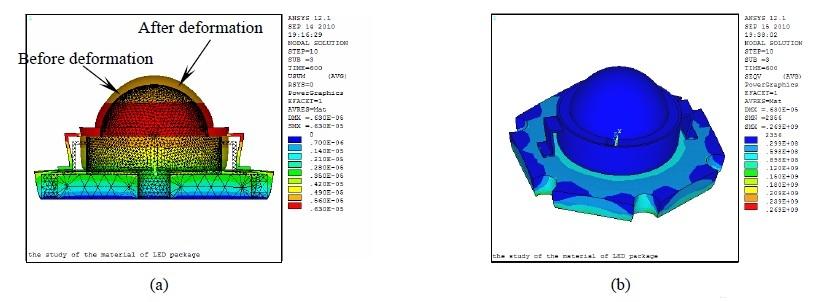
圖4 Lumileds 1 W LED 的熱變形云圖(a)和等效應力云圖(b)
[page]
圖6(a)是鍵合層等效應力分布云圖。由圖可見,最大熱應力在鍵合層邊角處為269 MPa,鍵合層最小應力也達到94.6 MPa。這是由于鍵合層導熱系數較小,熱阻較大,熱量在此處積聚較多,導致在鍵合層邊角處熱應力成為整個封裝器件最集中部分。圖6(b)是芯片等效熱應力分布云圖,芯片最大應力在四個邊角處為34.1 MPa,如此高的應力易引起芯片破裂,要特別注意。

圖6 Lumileds 1 W LED 鍵合層(a)和芯片(b)的等效熱應力分布
芯片頂面中心節點的位移隨時間變化曲線如圖7 所示,X 和Z 方向位移近似為零,Y 方向的位移隨著時間和溫度場的變化而不斷變化(Y 向為器件縱向即溫度傳遞方向),在光源點亮500 s 左右后,溫度場進入穩定狀態,此時芯片應變量達到最大6.3 μm,與瞬態溫度場的變化相符。
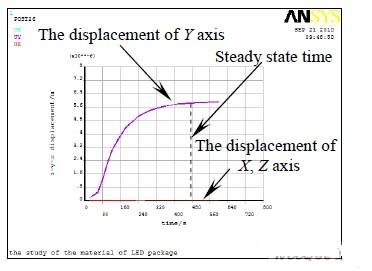
圖7 Lumileds 1 W LED 芯片中心節點位移隨著時間變化曲線
2.3 基板路徑上的熱應力、應變及剪應力的模擬與分析
在基板頂部平行于X 軸方向上選取如圖8 所示的一條軸向路徑,考察路徑上的應變、應力及剪應力的變化情況。
圖8 基板頂面上的路徑示意圖
[page]
圖9(a)表示的是路徑上X、Y、Z 三個方向的位移變化曲線。由圖可知,路徑上UZ 幾乎趨于零,Y 方向上,兩端形變較小,中間偏大,這與溫度場分布相符合;UX 兩端位移較大,往中間逐漸減小,且兩端關于中心對稱,這與基板的形狀與約束條件有關。圖9(b)為路徑上應力變化曲線,SX 與SZ 方向的應力變化趨勢相同,保持較高的應力水平,而SY 一直保持較低應力水平。X、Y、Z 三個方向顯示應力值都是兩邊大于中間,可以看出最大的應力出現在邊角處。
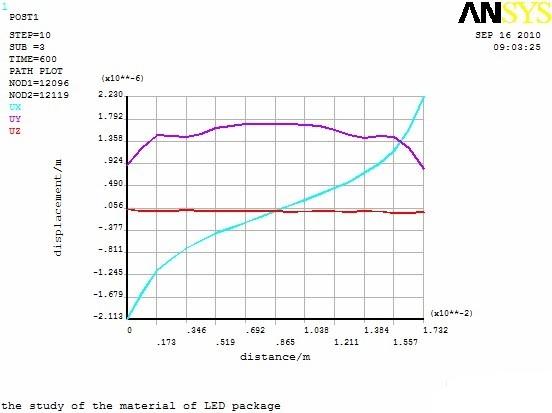
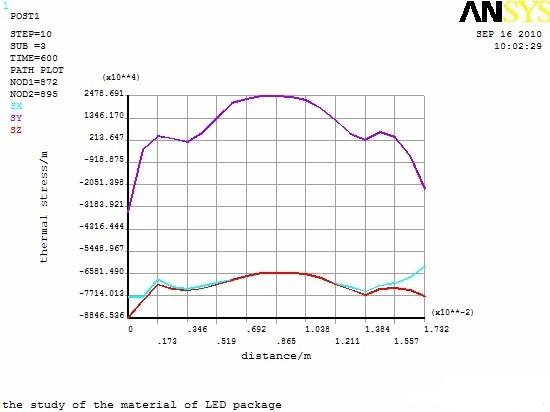
圖9 路徑上的位移(a)和應力(b)變化曲線
圖10 顯示了路徑上剪應力的變化情況,SYZ 與SXZ 幾乎重合,且剪應力很小,變化平緩;SXY 變化非常劇烈,說明在Y 方向上,即基板與熱沉之間有較大的剪應力,且由中間向兩端增大,表明剪應力主要集中在邊角區域。這是由于基板與熱沉為兩種不同的材料,材料之間的熱膨脹系數及彈性模量不同而產生較大剪應力。
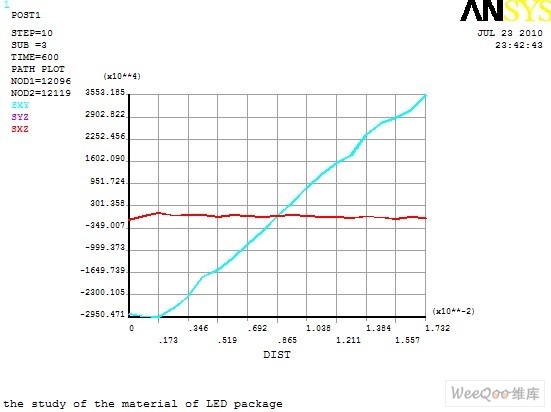
圖10 路徑上剪應力的變化曲線
[page]
2.4 材料導熱系數對應力,應變和溫度的影響
圖11 表示LED 結溫隨著器件各層材料導熱系數變化趨勢。
由圖可知,LED 結溫隨著熱沉和鍵合層導熱系數的變化趨勢類似,當λ 較小時,隨著λ 增大,結溫迅速降低;當λ 較大時,隨著各種材料導熱系數變化,結溫變化平緩。這是因為當λ 較小時,各材料的熱阻較大,而當λ 較大時,熱阻減小,熱量能順利傳出,此時導熱系數不再是影響整個系統傳熱效果的主要因素。由于LED 傳熱并不經過透鏡,所以透鏡的導熱系數對LED 的結溫變化影響很小。
圖12 表示LED 芯片最大等效熱應力及最大應變,隨著鍵合層導熱系數的變化。芯片的應變幾乎不變,與導熱系數無關;而芯片受到的熱應力隨著導熱系數增大迅速減小,但增大到一定值后,熱應力變化趨于平緩,與鍵合層導熱系數改變對溫度場的影響趨勢相吻合。這是由于整個傳熱過程中,鍵合層的導熱系數最低,芯片到熱沉熱阻較大,導致LED 結溫較高,溫度梯度較大,使得熱應力比較集中,因此鍵合層的材料選取對改變LED 結溫和熱應力有至關重要的作用。
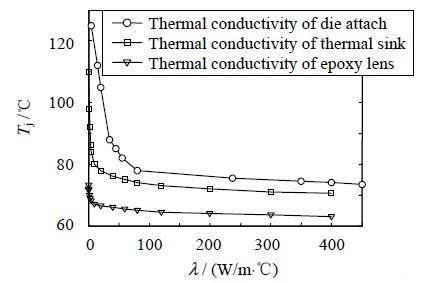
圖11 LED 結溫隨各種材料導熱系數變化曲線
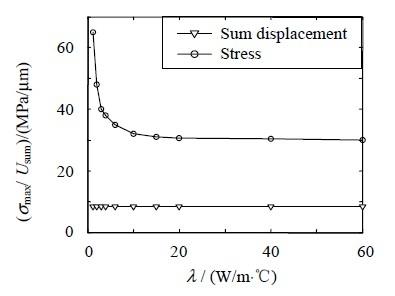
圖12 LED 芯片最大應力及應變隨著鍵合層導熱系數變化曲線
3 結 論
通過對功率型LED 器件的溫度場與應力場的模擬計算表明:LED 芯片軸向的應變與溫度場的變化情況相符合,在500 s 時趨于穩定;最大變形在透鏡與熱沉接觸地方,為6.3 μm;最大熱應力在鍵合層與芯片接觸的邊角處,為269 MPa,芯片的最大應力為34.1 MPa。通過材料對LED 結溫與應變的分析,得到LED 的結溫隨著鍵合層和熱沉的導熱系數增大先急劇減小,但增大到一定值后,LED 結溫變化趨于平緩,而透鏡導熱系數對結溫幾乎沒有影響;LED 的最大等效應力隨著鍵合層導熱系數的變化與溫度場變化情況完全相符合,對芯片的應變幾乎沒有任何影響。應變與應力主要集中在溫度梯度變化較大、受約束的面以及容易產生應力集中的邊角區域,這些區域特別容易產生破壞,因此LED 封裝時,必須考慮到實際工作溫度,要求材料必須能夠忍耐熱應力集中的地方。
根據本文的分析結論,LED 熱應力的產生主要是由于各層封裝材料之間的熱力學性能參數不同而引起的。為了提高LED 的封裝品質,需選擇合適的封裝材料,具備足夠大的導熱系數,以減小各封裝層之間的傳熱熱阻,防止熱量的積聚而產生大應力。為了避免LED 半導體器件產生大變形,各層封裝材料的熱膨脹系數差異要小。同時,各封裝層邊角處最好不要形成銳角,以避免在邊角處產生集中應力而破壞LED 器件。







