【導讀】定向耦合器在許多微波和毫米波系統中起著重要作用。例如,矢量網絡分析儀(VNA)使用定向耦合器來分離和采樣往返于DUT端口的前后波。在本文中,我們將討論耦合器的方向性系數如何在測量反射功率時引入誤差。
定向耦合器是測試射頻系統的寶貴工具。然而,這些設備的有限方向性可能會導致測量不確定性。本文將詳細介紹。
定向耦合器在許多微波和毫米波系統中起著重要作用。例如,矢量網絡分析儀(VNA)使用定向耦合器來分離和采樣往返于DUT端口的前后波。在本文中,我們將討論耦合器的方向性系數如何在測量反射功率時引入誤差。
測量反射功率
圖1展示了一個通用的定向耦合器,用于測量未知終端的反射功率。由于我們測量的是反射功率,因此耦合器的負載端(端口1)被標記為輸入端口,即使源端連接到端口2。
使用定向耦合器測量反射功率。顯示了所有四個端口,但隔離端口已端接。
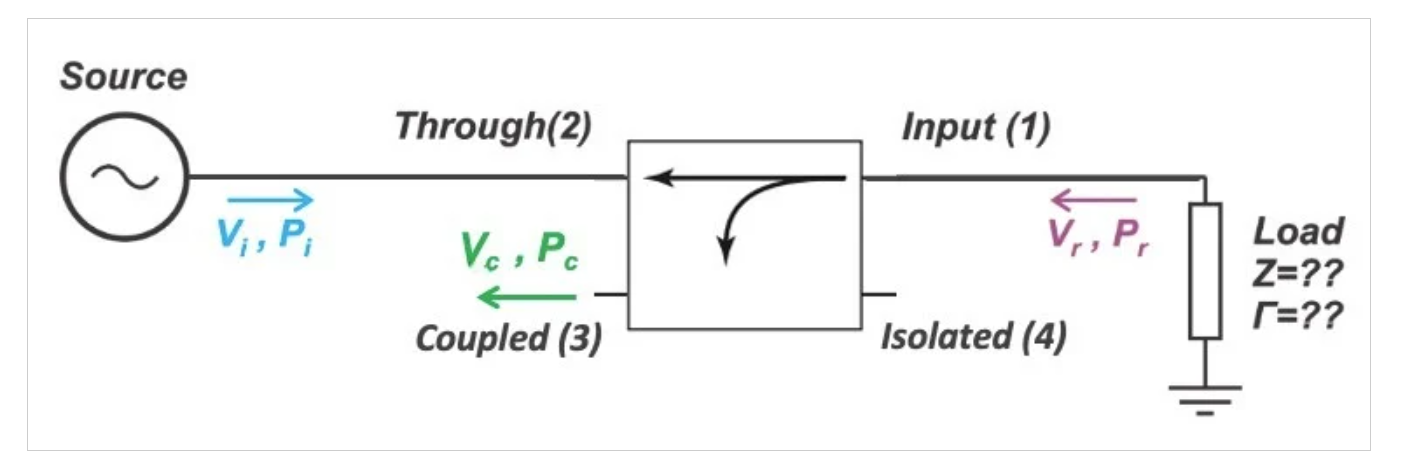
圖1.使用四端口定向耦合器測量反射功率。圖片由Steve Arar提供
電源提供的功率(Pi)通過耦合器傳輸到負載——從端口2到端口1。在負載處,一部分功率被反射回耦合器。反射功率(Pr)的量是負載阻抗和互連特性阻抗之差的函數。Pr的一小部分通過耦合器傳輸,并通過耦合端口端口3退出。
在理想世界中,知道Pi并測量耦合功率(Pc)將使我們能夠確定負載反射系數(Γ)。例如,如果負載完全匹配,則沒有功率被反射,因此Pc理論上應為零。
然而,現實世界中的定向耦合器會將端口 2 上入射的 Pi 泄漏到耦合端口 3,這會影響功率測量的準確性。泄漏量取決于耦合器的方向性。在本文的其余部分,我們將研究如何量化此誤差。
定向耦合器方程綜述
在本系列的前一篇文章中,我們介紹了通常用于表征定向耦合器的三個因素:
耦合系數(C)。
方向性系數(D)。
隔離系數(I)。
對于圖1中的四端口定向耦合器,我們可以計算出這些量如下:
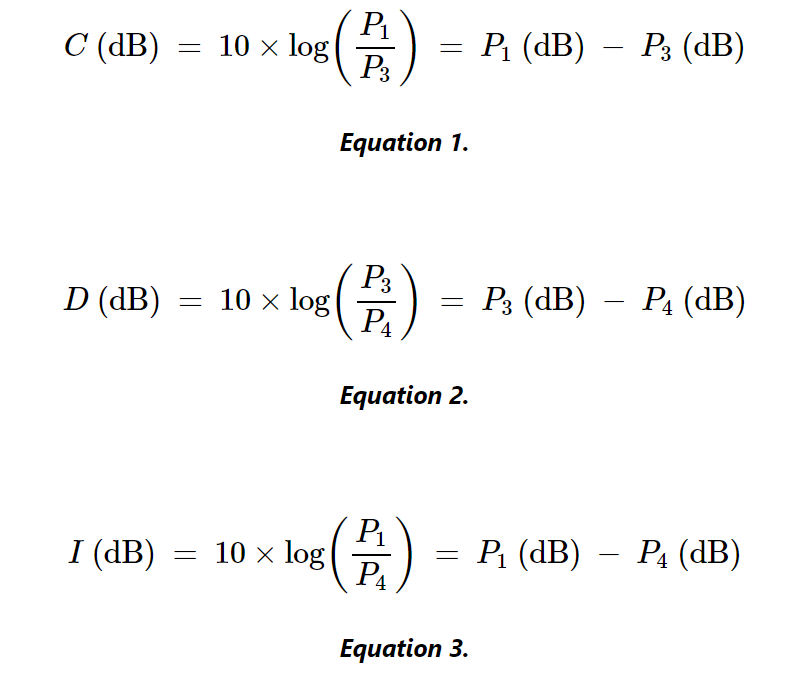
方程式1 方程式2 方程式3
Px是港口x的功率,單位為瓦特。
Px(dB)是端口x的功率,單位為dB。
這三個因素之間存在有趣的關系:
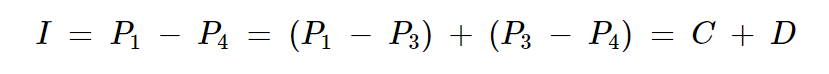
方程式4
計算耦合端口處的反射功率
首先,我們將計算到達耦合端口3的理想功率。假設來自源(Pi)和入射到端口2的所有功率都從端口1流出。從負載(Pr)反射的功率(dB)等于入射功率(Pi)減去負載的回波損耗(RL):
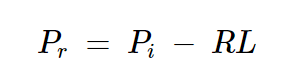
方程式5
端口1上輸入功率的一部分被耦合到端口3。通過重新排列方程2,我們可以表示端口3的耦合功率為:
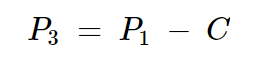
方程式6
我們將端口 3 的耦合功率稱為 Pc1。現在,通過將 Pr 替換為 P1,我們得到:
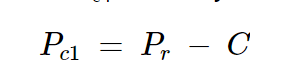
方程式7
最后,將方程5代入方程7,得到:
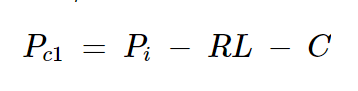
方程式8
圖2顯示了功率項、耦合因子和回波損耗之間的關系。
定向耦合器的功率項、耦合因子和回波損耗之間的關系。

圖2:功率項、耦合因子和回波損耗之間的關系。圖片由Steve Arar提供
多重反射讓事情變得更加困難!
在此分析中,我們假設從負載反射并通過耦合器的功率被耦合器的輸入端口(端口1)完全吸收。在實踐中,該端口可能不是完全匹配的。因此,耦合器和負載之間可能發生多次反射,進一步改變了測量誤差。
有限方向性引起的功率測量誤差的計算
現在我們需要開始考慮耦合器中的誤差來源。由于耦合器具有有限的指向性,因此Pi的一小部分也會泄漏到端口3。我們將這種泄漏稱為Pc2。
對于入射到端口2的波,端口3是隔離端口。因此,泄漏量由隔離因子表征,其方程略有不同:
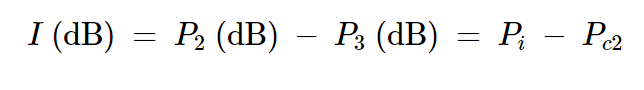
方程式9
重新排列這個方程并代入方程4,我們得到:
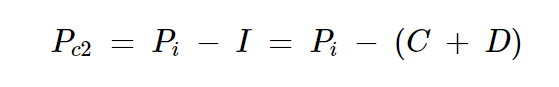
方程式10
圖3顯示了這組關系。Pc1是指定負載回波損耗的期望信號,Pc2是從端口2泄漏到端口3的信號。
反射功率測量中耦合功率和泄漏功率的關系。
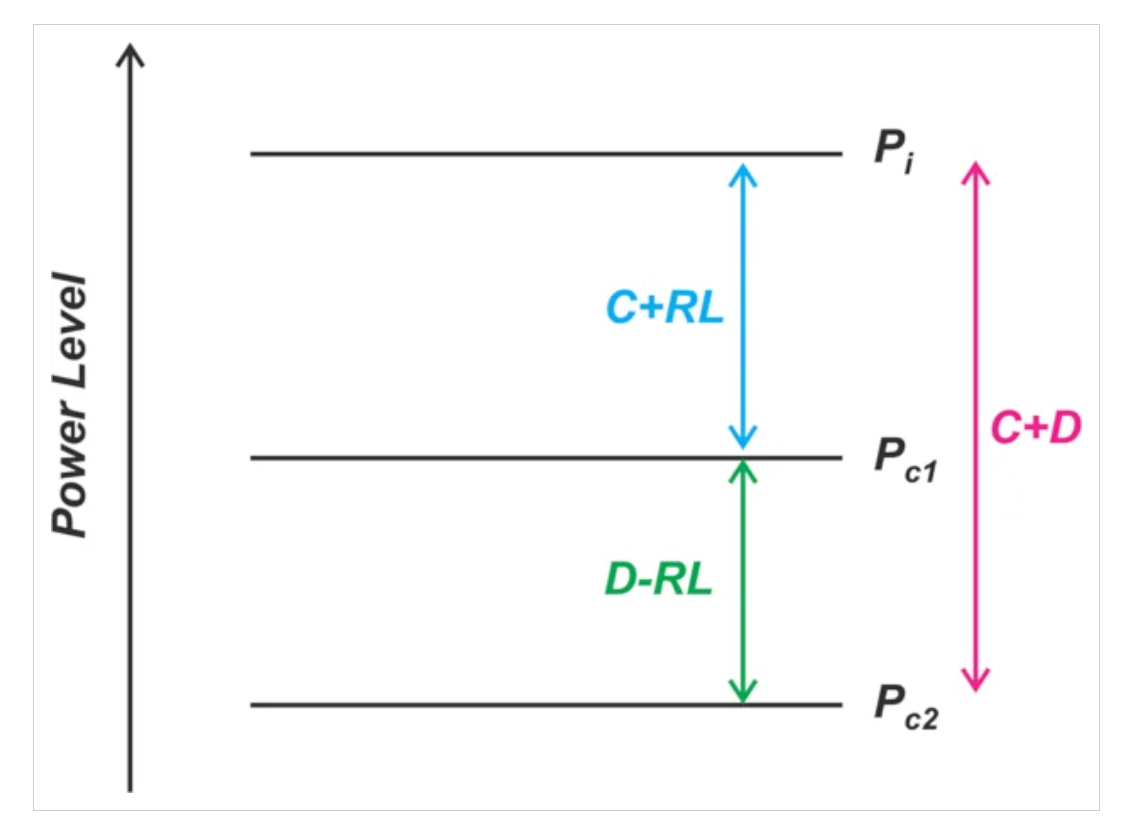
圖3.反射功率測量中耦合功率和泄漏功率的關系。圖片由Steve Arar提供
Pc2的存在僅是因為耦合器的有限方向性。理想情況下,方向性(D)將是無限的,測量的功率將僅是負載反射功率的函數。當D有限時,在耦合端口出現額外的功率項(Pc2),影響我們的測量精度。
如圖3所示,Pc1和Pc2之間的差值等于D – RL。考慮到方向性和回波損耗,我們可以很容易地確定Pc2相對于所需功率有多小。例如,如果D = 34 dB,RL = 26 dB,我們知道Pc2比Pc1低8 dB。
考慮相位差
上文中,我們確定了所需功率測量值(Pc1)與不希望泄漏(Pc2)之間的關系。然而,在耦合端口測量的總功率還取決于這兩個信號分量之間的相位差。
假設與Pc1和Pc2對應的電壓信號分別是振幅為a和b的正弦波形。使用圖3中所示的關系,我們有:
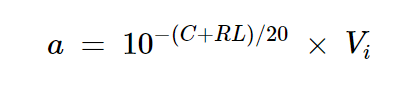
方程式11
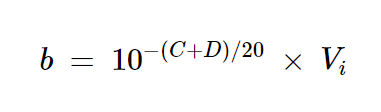
方程式12
其中Vi是圖1中電源入射電壓的振幅。
如果兩個信號同相,則總信號幅度為+b。另一方面,如果兩個信號相位相差180度,則總幅度為-b。這兩個極端情況給出了總信號的最大值和最小值——相位差的其它值產生的幅度介于a-b和a+b之間。
耦合端口處的總電壓波可以表示為:
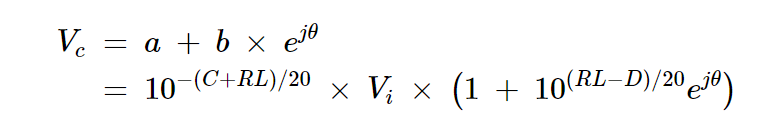
方程式13
方程式13中的術語可以理解為:
ejθ這一術語表示兩個信號之間的相位差。
括號內的術語是誤差系數,表示測量值與實際值的相對偏差。
括號前面的術語表示如果耦合器具有無限方向性,我們將獲得的期望幅度。
我們將把這種期望振幅稱為Vdesired,并分別寫出它的方程式:
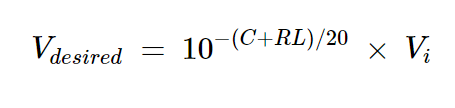
方程式14
然后我們可以將方程式13重寫為:
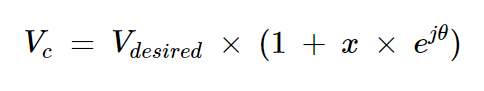
方程式15
其中x等于10(RL-D)/20。總誤差因子是1和x的矢量和。圖4幫助我們直觀地展示了誤差項。
誤差因子,可視化為具有實部和虛部的向量。
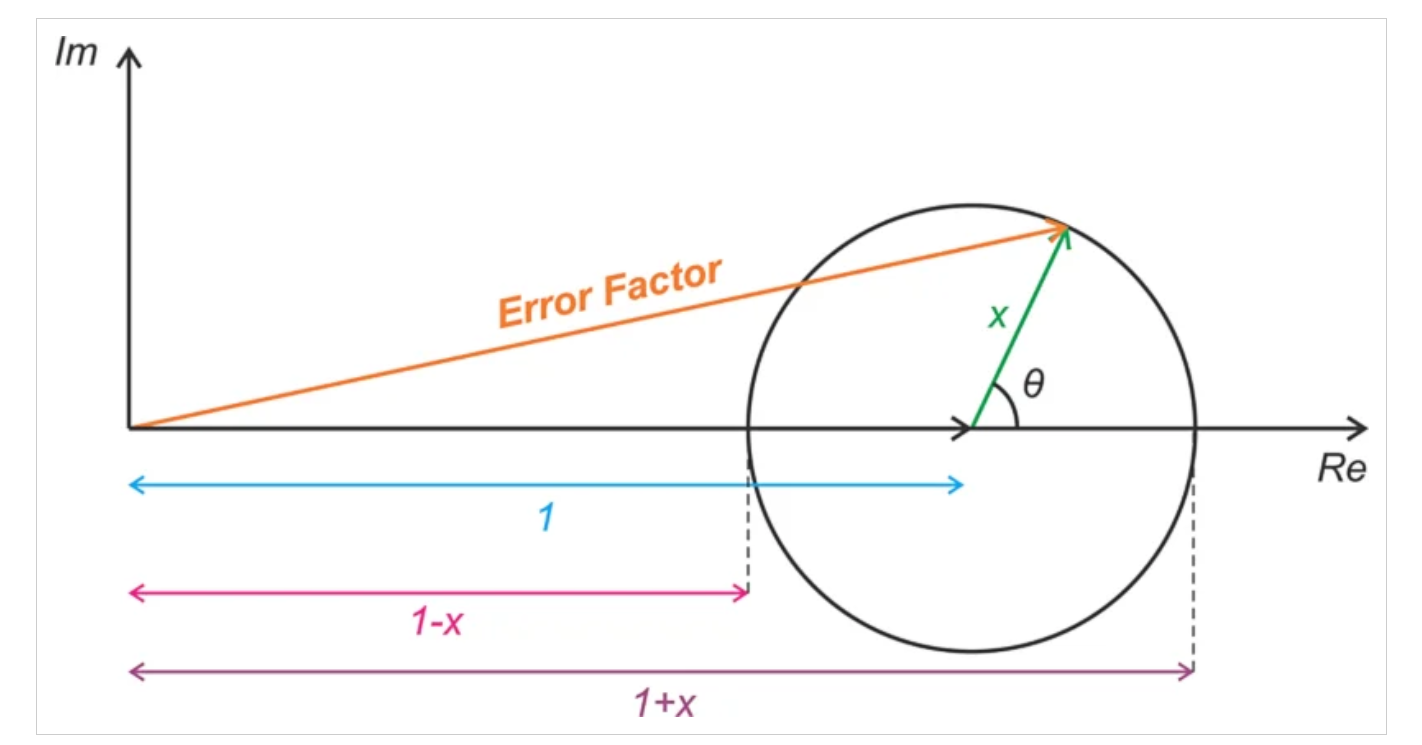
圖4.將誤差因子可視化為一組具有實部和虛部的向量。圖片由Steve Arar提供
示例1:計算測量回波損耗的不確定性
為了澄清上述討論,讓我們來解決羅德與施瓦茨公司關于VNA基礎的文檔中的一個示例問題。在這個例子中,我們的目標是使用方向性(D)為40 dB的耦合器來測量實際回波損耗(RL)為30 dB的負載。測量的回波損耗的最大值和最小值是多少?
從圖3中,我們知道所需信號功率和不想要的信號功率之間的差值等于D – RL = 40 - 30 = 10 dB。因此,不想要的電壓的幅度比所需的電壓小0.32倍,計算如下:
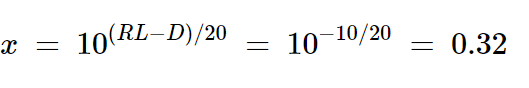
方程式16
將x的這一值代入方程式15,我們看到總電壓可以為:
系數1+x=1.32,比實際值高。
系數1-x=0.68,低于實際值。
因此,測量的功率可以是:
20log(1.32) = 比實際值高2.4 dB。
20log(0.68) = 比實際值低3.35 dB。
測量的反射功率與負載的回波損耗有關。反射功率越高,回波損耗越小。當測量的反射功率比實際值高2.4 dB時,測量的回波損耗比實際值低2.4 dB。這導致:
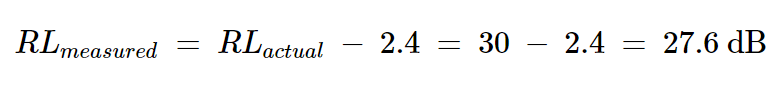
方程式17
同樣,當測量的反射功率比實際值低3.35 dB時,測量的回波損耗為30 + 3.35 = 33.35 dB。因此,測量的回波損耗可以在27.6 dB和33.35 dB之間。
示例2:計算測量回波損耗的不確定性
為了更好地理解這些計算,讓我們來看另一個例子。假設我們的目標是使用方向性為35 dB的方向耦合器來測量實際回波損耗為20 dB的負載。按照與上述示例類似的過程,我們首先找到不期望電壓的幅度相對于期望電壓有多小:
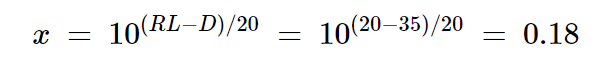
方程式18
總電壓可以是:
比實際值高1 + 0.18 = 1.18倍。
系數1 - 0.18 = 0.82,低于實際值。
因此,測量的功率可以是:
20log(1.18) = 比實際值高1.44 dB。
20log(0.82) = 比實際值低1.72 dB。
當測量的反射功率比實際值高 1.44 dB 時,測量的回波損耗為 20 – 1.44 = 18.56 dB。另一方面,當功率測量為低 1.72 dB 時,測量的回波損耗為 20 + 1.72 = 21.72 dB。因此,測量的回波損耗可以在 18.56 dB 和 21.72 dB 之間。
誤差如何隨回波損耗和方向性變化?
圖5顯示了不同回波損耗和方向性值下反射功率測量誤差。
反射功率測量誤差是回波損耗和方向性的函數。
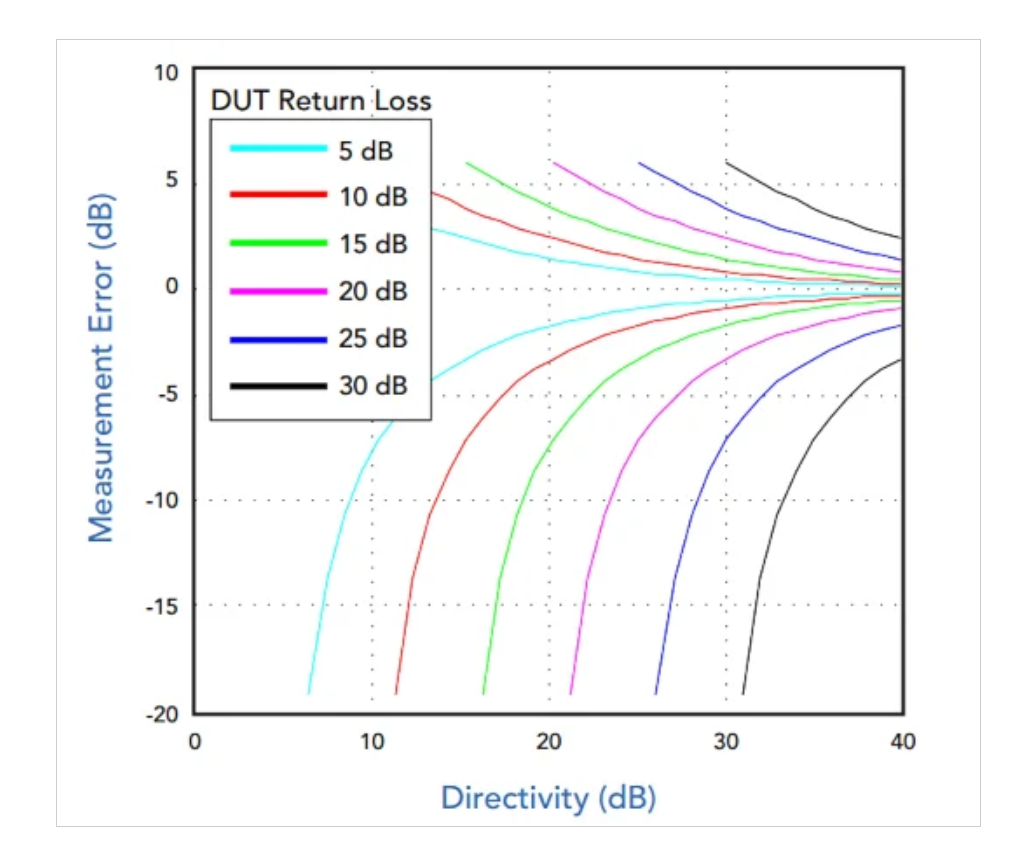
圖5.反射功率測量誤差與回波損耗和方向性的關系。圖片由Marki Microwave提供
上述曲線對應于插入損耗為1 dB的耦合器。這使得結果與我們的分析結果略有不同,在我們的分析中忽略了耦合器的插入損耗。然而,該曲線揭示了有限方向性引入的誤差的一些重要特性。
首先,請注意,誤差隨著回波損耗的增加而增加。對于給定的輸入功率(Pi),泄漏功率是恒定的,但測量的信號(Pr)在減小。
其次,觀察到增加給定回波損耗的指向性可以減小誤差。圖3中的關系解釋了為什么:隨著D的增加,與期望信號相比,不期望信號變得越來越小,從而提高了測量精度。
圖5摘自Marki Microwave的白皮書,標題為“方向性和VSWR測量:了解回波損耗測量”,顯示了當方向性幾乎等于負載的回波損耗時誤差會變得非常大。白皮書建議,作為經驗法則,您可以通過使用比DUT回波損耗高約15 dB的方向性將誤差降低到約1 dB。例如,如果回波損耗為20 dB,我們需要35 dB的方向性將誤差限制在1 dB。
測量正向功率
我們還可以使用定向耦合器來對正向功率進行采樣,如圖6所示。
使用三端口定向耦合器對正向功率進行采樣。
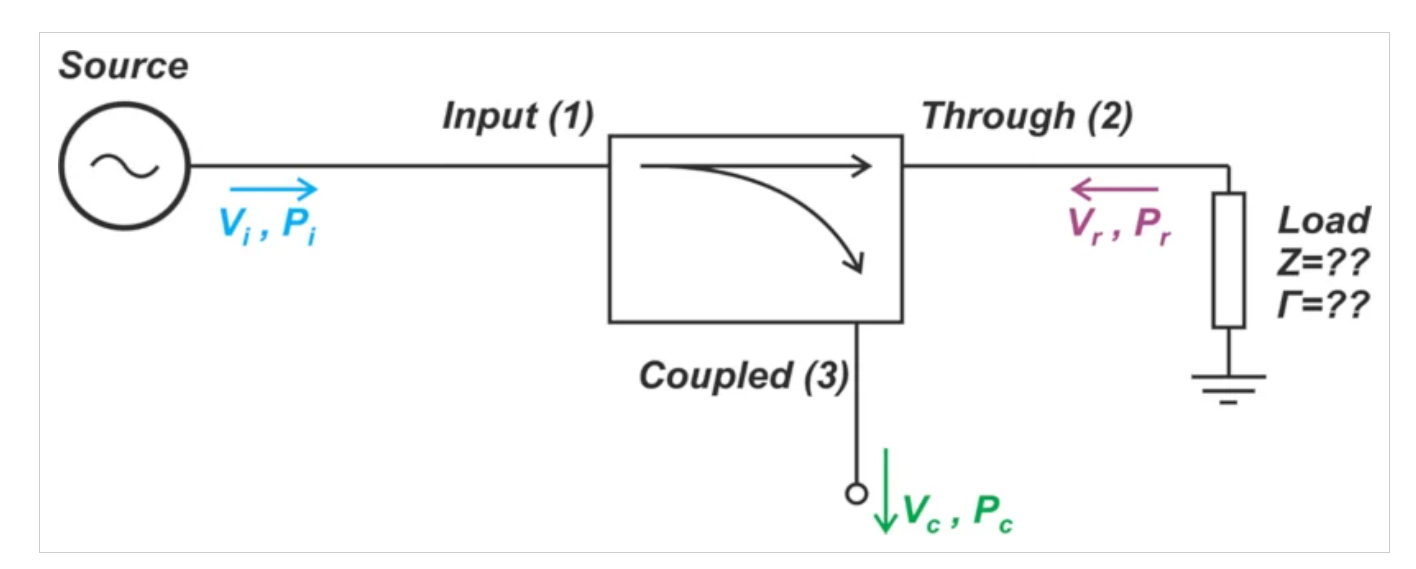
圖6.使用三端口耦合器對正向功率進行采樣。圖片由Steve Arar提供
與反射功率測量相比,耦合器對正向功率測量的方向性要求更寬松。這是因為被測量的輸入功率(Pi)大于反射功率(Pr)。圖7顯示了不同回波損耗和方向性值的前向功率測量誤差。
正向功率測量誤差是回波損耗和方向性的函數。
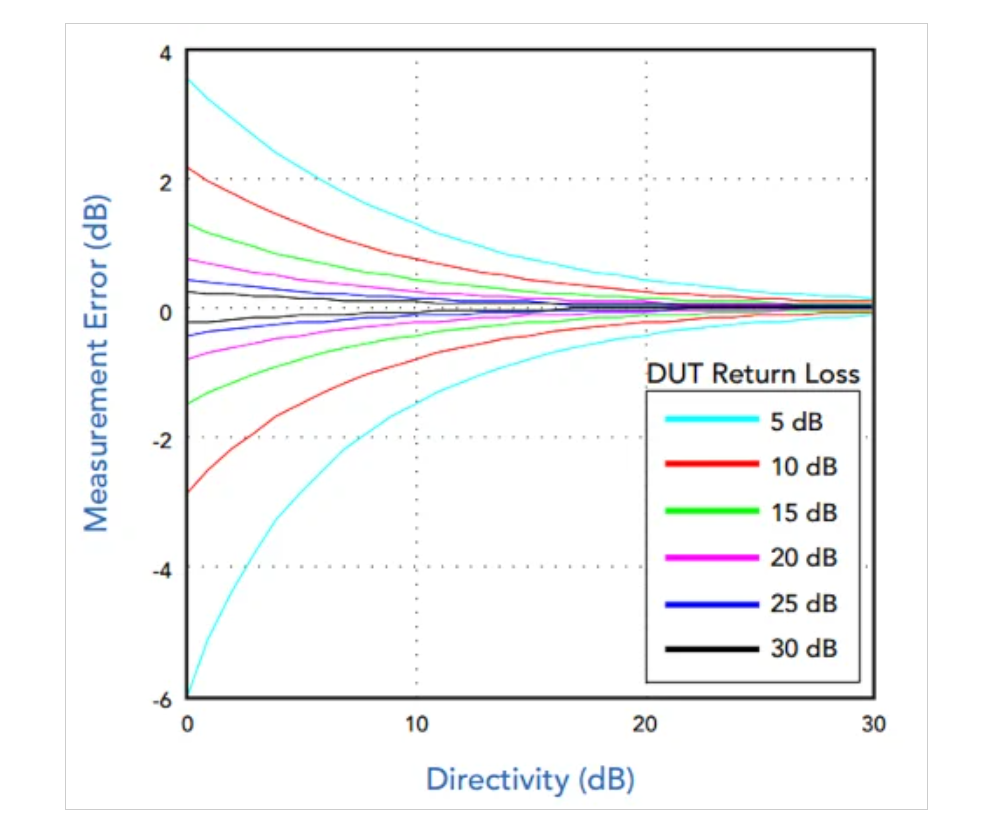
圖7. 正向功率測量誤差與回波損耗和方向性的關系。圖片由Marki Microwave提供
請注意,負載回波損耗越小,誤差就越大。這是因為較低的回波損耗意味著更多的功率被反射回源。這反過來導致耦合器輸出端的不期望信號增加。即使對于很小的回波損耗,15 dB的指向性也可以確保正向測量的誤差不超過大約1 dB。
耦合器方向性的測量
最后,由于它與本文中提供的誤差分析密切相關,我想提一個測量耦合器方向性的實用方法。我們通常不能直接測量這個方向性,因為前向和后向波在耦合器的輸出端產生了可比較的信號分量。
然而,我們可以修改圖1,使用滑動負載間接測量耦合器的方向性,如圖8所示。
測量耦合器方向性的電路。
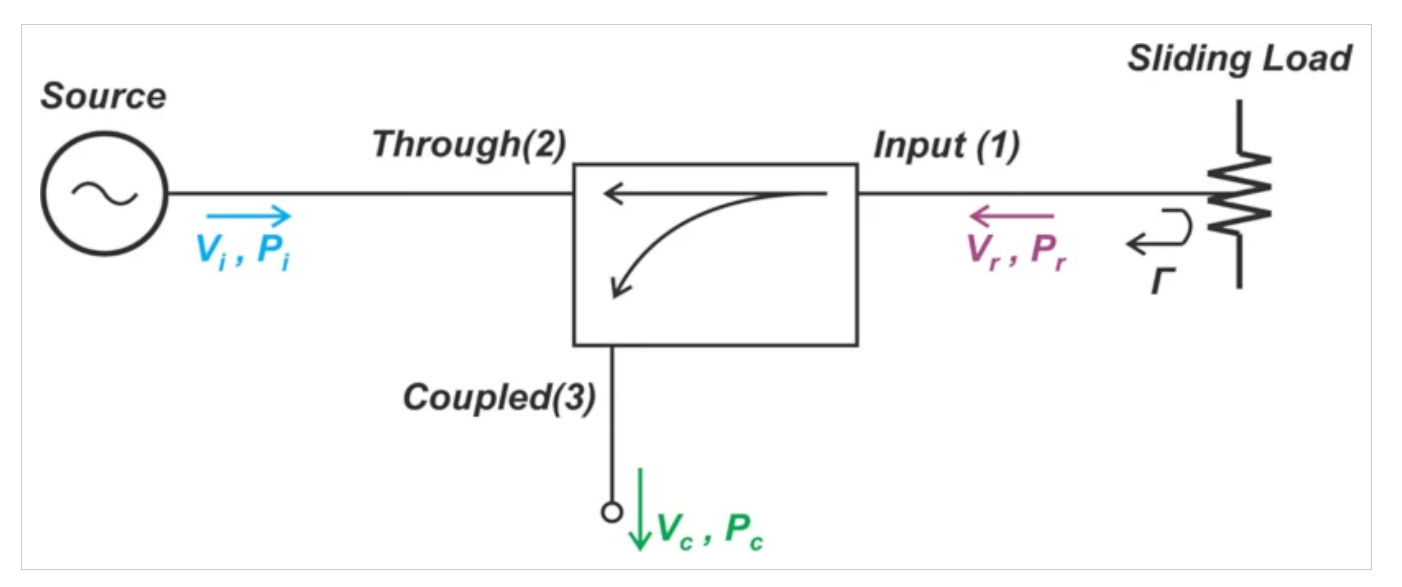
圖8.測量耦合器方向性的電路。圖片由Steve Arar提供
改變滑動負載的位置會在反射信號中引入可變相移。根據我們上面的討論,我們知道,當我們改變滑動負載的位置時,耦合端口處的電壓會產生圓形輪廓(圖4)。通過找到耦合端口處的最小和最大功率電平,我們可以確定耦合器的方向性。
免責聲明:本文為轉載文章,轉載此文目的在于傳遞更多信息,版權歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權問題,請聯系小編進行處理。
推薦閱讀:





