中心議題:
- 逆變器模型分析
- PID控制器與重復控制器設計
解決方案:
- 串聯拓撲結構的重復控制器設計方案
PID控制作為一種經典控制算法,具有結構簡單、易于調試、動態響應特性快、魯棒性強等特點。但是,對于中、低頻周期信號,該算法仍無法實現無靜差控制;對由非線性負載引起的輸出波形畸變的調節能力也較差。本文介紹了一種PID控制器與重復控制器采用串聯拓撲結構的方案,將穩定的PID+控制對象閉環系統作為重復控制器的控制對象,在保證系統穩態誤差和動態性能的同時,簡化了重復控制器的設計。
逆變器模型

式中,u0為輸出電壓;i 為電感電流; 為負載電阻;C為濾波器電容;£為電容等效串聯電阻:
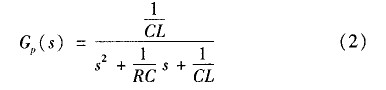
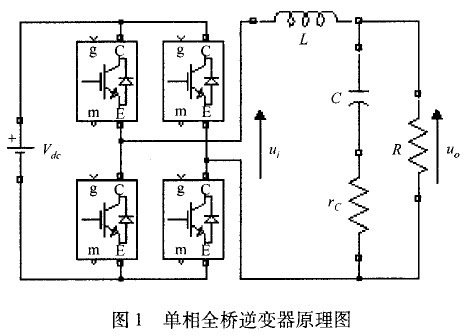
取采樣頻率和開關頻率相等,把逆變橋看作一個零階保持器,將式(2)離散化可得對象的脈沖傳遞函數為:
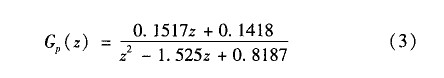
PID控制器設計
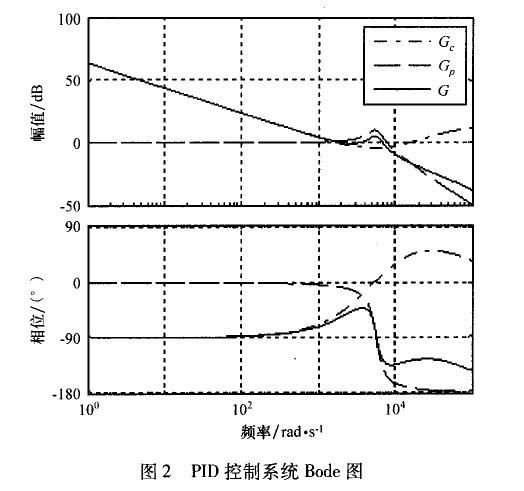
圖2所示為PID控制系統的開環頻率特性圖(Bode圖)。其中,G0為被控對象;G 為PID控制器;G=Gp×G0
按照傳統PID設計理論,首先設開環系數為K=200,目的是提高系統低頻增益,減小穩態誤差。但是K值過大會降低系統穩定性,所以在低頻段處加一零點,與積分環節構成滯后校正。該滯后環節的作用主要有兩條:一是在保證系統暫態性能基本不變的情況下,提高系統低頻響應的增益,減小系統的穩態誤差;二是利用其低通濾波特性衰減系統高頻響應增益,提高系統的相角裕度,以改善系統的穩定性。
在中頻段60 處加一零點,同時在高頻段 處加一極點,由此構成超前校正。其作用主要有兩條:一是利用相角超前特性增大系統的相角裕度,提高系統的截止頻率,保證系統快速的動態響應;二是衰減系統高頻響應增益,抑制高頻噪聲,提高系統魯棒性。
圖2中G為PID控制系統開環傳遞函數,由其頻率特性曲線可以看到,系統低頻開環增益非常大;截止頻率附近頻段相角裕度增大;高頻段開環增益很小,抑制了高頻干擾信號。通過滯后一超前相校正方法對PID控制器進行設計,達到了預期的目的。經過以上分析,PID傳遞函數為:
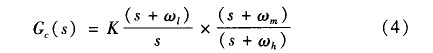
取采樣頻率和開關頻率相等,采用零階保持器將式(4)離散化可得對象的脈沖傳遞函數:
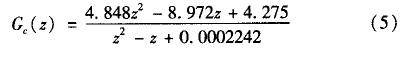 [page]
[page]
重復控制器設計
根據內模原理,在閉環系統中加入外部周期信號動態模型,則系統可以達到對外部周期信號漸近跟蹤的目的,重復控制策略正是基于這一原理。圖3為基本重復控制器系統結構圖,其中重復控制器離散表達式為:
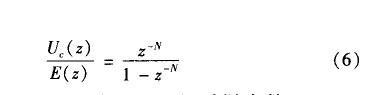
式中,Ⅳ為每基波周期對輸出電壓的采樣次數。
由式(6)可知,當頻率為∞=2~k/T(K=0,1,2,……, T為基波周期),由于z=1,所以若在閉環系統中嵌入重復控制器,將使開環增益趨向無窮大。在這種情況下,非諧波輸入信號將被強烈衰減,達到精確跟蹤輸入信號的目的。但是,由于無法精確知道控制對象動態特性,所以開環增益趨向無窮大將惡化閉環系統的穩定性。為了保證系統穩定性,需對基本重復控制系統改進。
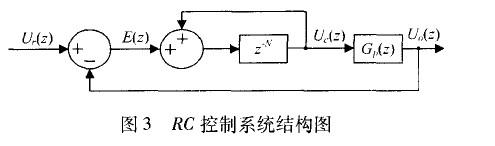
本方案提出的復合重復控制系統結構圖如圖4所示。
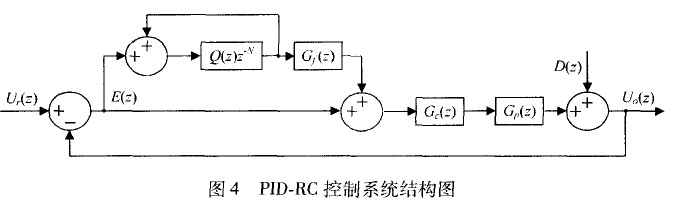
Q(z)、Gf(z)為低通濾波補償器,是重復控制器設計工作的重點。P(z)的作用是將開環增益調節至很大的有限值,在不影響穩態精度的前提下保證系統穩定性;Gc(z)的作用是通過限制重復控制器的頻帶范圍來提高系統的魯棒性 。由圖可得到系統的誤差傳遞函數為:
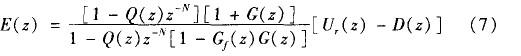
式中,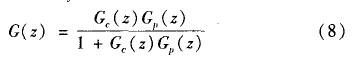
根據小增益定理,上述系統穩定的條件是:
① 閉環系統Gf(z)是穩定的。
②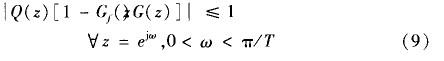
由誤差傳遞函數式(7)可知,如果:
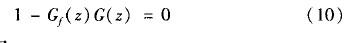
則式(7)可重列為:
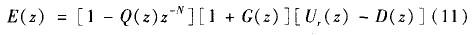
如果通過構造Q(z),在頻率∞=2,rrk/T(k=0,1,2,……)處使:

則可以得到E(z)=0。所以,當系統滿足式(10),式(12)時,各階諧波的穩態誤差理論上將趨向零。但是,由于實際的系統為非理想系統,上述設計要求無法滿足所有頻段的諧波,通常是在一定頻率范圍內,根據穩定性條件式(8)、式(9)和控制器條件式(10),式(12)設計重復控制器,滿足系統對穩態和動態的要求。
根據式(8)、式(10),補償器Gf(z)可以直接設計為G(z)的逆函數。但是,如果G(z)是非最小相位系統,雖然式(10)仍成立,外部表現穩定,由于有不穩定零極點對消情況,這將導致系統內部不穩定。這種情況下,必須采用其他類型的補償器對Gf(z)進行設計。
本文中提出的方案,控制對象是PID控制器鎮定的穩定閉環系統,其本身即為最小相位系統,所以可以直接使用逆函數設計補償器,即:

式(12)理論上要求p(z)=1;然而式(9)表明,由于高頻段G(z)趨向0,Q(z)在高頻段應小于1,所以Q(z)應是一個具有零相移的低通濾波器,其表達式為:
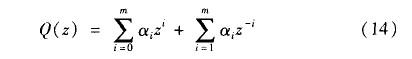
實際應用中,采用一階低通濾波器完全可以滿足系統要求:
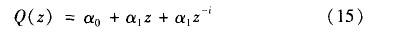
通過以上分析,現在重復控制器的兩個濾波器可以根據式(13)、式(15)設計。[page]
為了進一步理解重復控制器在系統中的作用,可以比較嵌入重復控制器和沒有嵌入兩種情況下的系統開環頻率特性,如圖5所示。
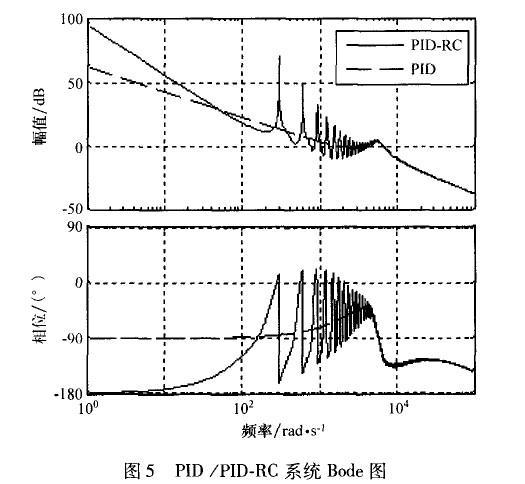
在高頻段,開環增益變得非常小,這對抑制高頻噪聲,提高系統穩定性和魯棒性是非常有幫助的。但是,在非諧波頻率處,沒有嵌入重復控制器的系統開環增益更大一些,這說明重復控制器對位于該頻率的信號控制效果較差。因此,PID控制器在系統中除了有提高系統動態響應速度的作用外,還要調節非諧波信號,彌補重復控制器的不足。
仿真實驗分析
根據以上分析,筆者對數字PID控制、重復控制以及提出的復合控制進行了仿真實驗。系統參數如下:
輸入直流電壓為270 V,輸出交流電壓為110 V/50Hz,開關頻率為10 kHz,輸出濾波電感為1.5 mH,輸出濾波電容為20 F,負載電阻為10 n。
圖6,圖7中,Ur為給定電壓;Uo為輸出電壓。
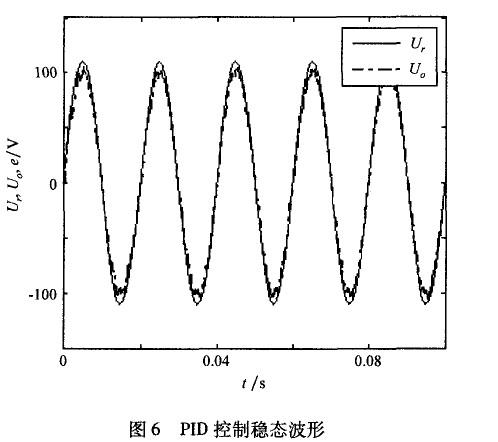
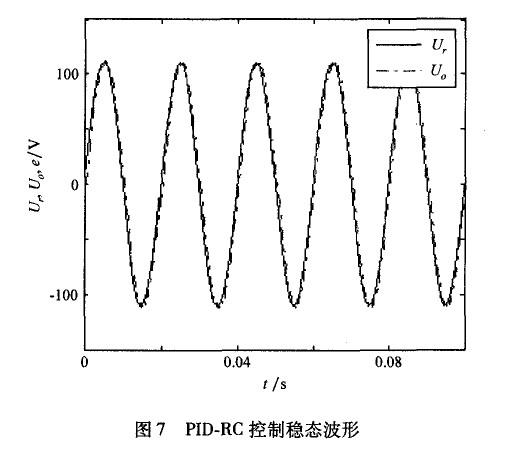
PID控制對于周期性信號無法做到無差跟蹤,存在周期性穩態誤差。嵌人了重復控制器的系統,輸出能夠很好地跟蹤輸入信號,系統迅速進入穩態,表現出良好的動態性能。
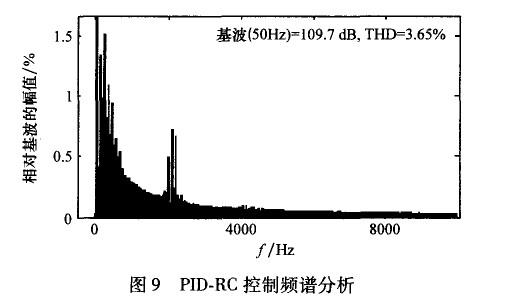
圖8,圖9為系統輸出電壓波形的頻譜分析。圖中直觀地反映出重復控制可以有效地抑制諧波,降低輸出波形的畸變率。
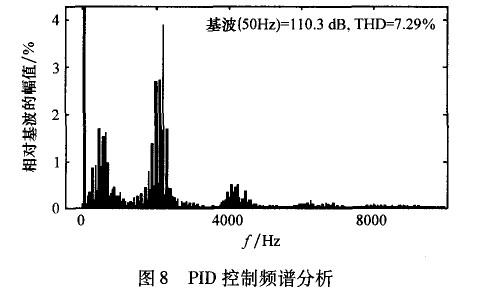
結語
上述過程較為詳細地分析了重復控制器的工作原理,結合PID控制和重復控制各自的優缺點,設計了具有串聯拓撲結構的復合控制器,同時發揮了重復控制器對周期信號無差跟蹤能力和PID控制器對突變干擾的快速響應能力。仿真實驗結果證明,重復控制對削減輸出波形畸變是有效的,基于PID控制和重復控制的復合控制策略是一種實用的正弦波逆變器控制方案。








