中心議題:
- 三相電壓型PWM整流器的非線性控制研究
- 運用Matlab進行仿真研究PWM整流器電流的任意控制
- 采用非線性控制時PWMΩ整流器的響應
1 引 言
由于PWM整流器與傳統的不控整流器和相控整流器相比較,具有單位功率因數、網側電流正弦化、能量可能實現雙向流動等優點,因此,PWM整流器的發展和 應用將成為主流。隨著對PWM整流器模型的不斷改進和對PWM整流器認識的不斷加深,建立了PWM整流器的非線性模型,這不僅很好地體現了PWM整流器的 非線性特性,而且為將非線性控制理論應用到PWM整流器奠定了良好的基礎。本文就是在試圖將非線性控制理論中的狀態反饋線性化方法引入到PWM整流器的控 制方面作一下探討。
2 三相電壓型PWM整流器的數學模型
圖1是三相PWM整流器的拓樸結構,功率開關按采用的調制方式動作,由于輸入電感的濾波作用,整流器交流側可近似認為是三相正弦電流;直流側有大電容穩 壓,輸出呈直流電壓源特性,穩態時輸出直流母線電壓可保持不變,一般情況下,要求控制輸入電流與輸入電壓同相位,通常采用電壓外環和電流內環的雙環控制方 式,電壓外環主要是保證直流輸出電壓穩定,電流內環主要是按電壓外環輸出的電流指令進行電流控制,如實現單位功率因素正弦波電流控制。
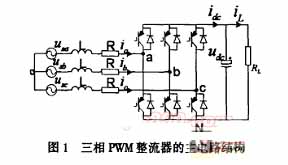
圖1中,


式中


為了獲得良好的控制性能,對(1)進行d-q坐標變換,得到其d-q模型:

[page]
從功率平衡的角度考慮(2)式的第三個式子,則有:

于是有

因此,三相電壓型PWM整流器的非線性模型亦可描述為:

上述所得到的數學模型(式(5))表明系統為多輸入多輸出(MIMO)非線性系統。此系統可以用如下的狀態矩陣形式表示:

其中X和U分別為狀態變量和控制變量。選擇狀態變量

于是,三相電壓型PWM整流器的狀態矩陣形式可寫為:

其中:

從而可以得到狀態空間形式下的三相電壓型PWM整流器的控制框圖,如圖2所示。

[page]
3 狀態反饋非線性控制原理
對非線性系統:

進行輸入輸出線性化的過程為:重復對輸出y進行微分,直至輸入u首次出現,即:

其中,



使輸出y和新的輸入v之間具有線性關系:

對于三相電壓型PWM整流器系統,由所得到的模型表明系統為多輸入多輸出系統,且具有兩個輸入量,因此便可能控制兩個輸出變量







為了應用狀態反饋將其線性化(輸入輸出線性化),必須要設定外部輸出的值,即兩個n階導數和m階導數。設

一旦將這兩個導數的值計算出來,便可以得到用來變換系統(1)的控制變量



假定在穩態時,有






于是,系數


[page]
將所采用的非線性控制原理概括如下:
應用式(7)來計算外部輸入



應用式(7)以及



4 系統仿真及結論
通過非線性控制模型,運用Matlab進行仿真研究PWM整流器電流的任意控制和采用非線性控制時PWMΩ整流器的響應。仿真系統參數為:




圖4給出了PWM整流器采用不同控制器時PWM整流器直流電壓的階躍響應,并對兩種控制器作了比較。仿真結果表明PWM整流器在采用非線性控制器后具有了更快的響應速度和較小的超調量。

圖5和圖6分別給出了非線性控制和線性控制下在t=0.01s時刻無功電流突變時的響應。從仿真結果可以看出,非線性控制時PWM整流器能夠將有功功率 和無功功率解耦運行,即在無功電流突變時,其直流側電壓不受影響;但是在線性控制時不能做到這一點。另一方面,非線性控制時PWM整流器無功電流



[page]
圖7給出了PWM整流器采用不同控制器在t=0.005s時刻負載突變時的響應。顯然,非線性控制時PWM整流器具有更好的抗擾。這也說明采用非線性控制器后,PWM整流器具有了更好的抗擾動性能。

5 結束語
在三相電壓型PWM整流器非線性模型(d-q模型)的基礎上,應用狀態反饋線性化方法設計出了應用于三相電壓型PWM整流器的非線性控制器,并對此非線 性控制器進行了仿真,并且與線性控制器進行了比較。仿真結果表明,與線性控制器相比較,非線性控制器設計具有更好的跟隨性能和更好的抗擾性能;并可實現有 功分量和無功分量的解耦運行。這還為PWM整流器的高性能應用提供了理論依據。








