【導讀】解析二相混合式步進電機高性能驅動控制方法,從而實現減小低頻振蕩和改善矩頻特性的目的。在常用升降速控制技術的基礎上,把指數形式結合臺階模式的加減速控制方法加以改進。以Logistic增長方程為模型,提出一種基于調頻調壓驅動模式的電流補償控制算法,即電機的供電電壓實時跟蹤運行頻率的驅動方式。實驗結果顯著改善低頻穩(wěn)定性和矩頻特性,具有一定的研究和經濟價值。
步進電機是一種數字電機,具有無累積誤差、性價比高等優(yōu)點,被廣泛應用于生活和生產領域中。異于其他電機,步進電機必須使用驅動器才能工作。步進電機運行時存在低頻振蕩和矩頻特性,是設計驅動系統時必須考慮的兩大難題。另外,步進動電機需要有升降速過程才能運行平穩(wěn)。起動時,如果加在電機上的脈沖信號頻率過高,則會出現失步或振蕩,電機會抖動并有呼嘯聲。驅動器的性能影響著步進電機的發(fā)展前景,因此研究一種高性能步進電機驅動方法具有重要的實際意義。
1 驅動系統的原理與設計
本系統的設計方案采用調頻調壓驅動方式,系統的硬件電路按功能來劃分,主要包含以STM32F103為核心的主控模塊、功率驅動電路、調頻調壓驅動電源和電機電流檢測模塊。基本框圖如圖1所示。
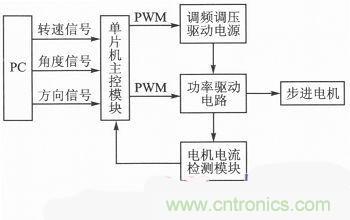
圖1:步進電機驅動系統原理框圖
驅動系統的核心是微處理器控制模塊。由STM32F103單片機及其外設電路組成,用于實現電機PWM時序信號的輸出、轉速和方向的控制、軟件控制算法的實現、與計算機通信等功能。增強型STM32單片機有80個GPIO口,高達72 MHz的內部時鐘頻率的定時器,通過改變PWM的頻率實現電機速度的變化,完全滿足驅動的設計要求。
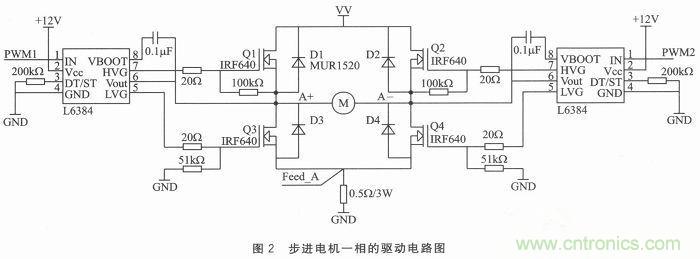
二相混合式步進電機需要雙極性驅動方式才能工作,即繞組在一個周期內需要有正反兩個方向的電流流過。采用H橋電路可以很容易解決電機雙向通電的問題,二相步進電機需要8個開關管構成兩個H橋,其中一相的H橋驅動電路如圖2所示。MOS管驅動采用驅動芯片L6384,2片L6384和4個功率MOSFET管IFR640構成H橋。Q1、Q4和Q2、Q3輪流導通,繞組中的電流方向在周期內不斷地改變。
二相混合式步進電機需要雙極性驅動方式才能工作,即繞組在一個周期內需要有正反兩個方向的電流流過。采用H橋電路可以很容易解決電機雙向通電的問題,二相步進電機需要8個開關管構成兩個H橋,其中一相的H橋驅動電路如圖2所示。MOS管驅動采用驅動芯片L6384,2片L6384和4個功率MOSFET管IFR640構成H橋。Q1、Q4和Q2、Q3輪流導通,繞組中的電流方向在周期內不斷地改變。
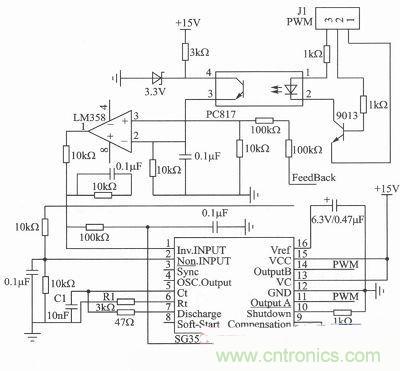
可調電源電路采用專用集成PWM控制芯片SG3525實現。調頻調壓電路如圖3所示,控制信號PWM由J1輸入,實現光耦調節(jié),與輸出信號共同反饋到SG3525的反相輸入端和補償端,用以改變11腳和14腳輸出的PWM的占空比,使得輸出穩(wěn)定。C1和R1為片內振蕩器外接電容、電阻,可設定輸出PWM波的斬波頻率,本系統斬波頻率為60 kHz。11和14腳輸出PWM控制后級功率管的“開”和“關”,實現繞組充放電,設計中采用220 V的市電輸入,輸出 0~60 V/4 A。
2 升降速控制方式
若m相步進電機驅動脈沖的頻率為f,轉子有Zr個齒,則電機的轉速可 其中c=f1-f0,f1=a/b,常數b決定f-t曲線的變化規(guī)律,同樣也影響加減速的快慢。式(6)通常作為理論推導的最合適的升降速控制曲線,即指數加減速曲線。指數曲線是矩頻特性的一種近似,能很好地利用低頻轉矩恒定的優(yōu)勢,但是高速加速時仍會出現轉矩大幅度下降,導致加速至高速困難。為更好地利用指數曲線的優(yōu)點,彌補指數曲線的缺陷,提出指數形式結合臺階模擬加減速方式和快速臺階模式減速方式。整個加速和減速過程如圖4所示。加速和減速采用不同的曲線控制。加速分為兩段,首先利用指數形式加速快的優(yōu)點,當達到一定速度時,再利用臺階模式加速,此處B點取目標頻率的80%,加速過程中的臺階比較密,易于電機加速;減速過程中只采用臺階形式減速,因為電機具有定位力轉矩特性,取fm的20%作為一個臺階,電機不會發(fā)生過沖,復雜的減速控制曲線反而會影響減速時間。
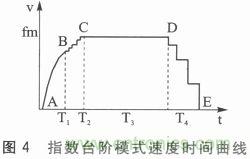
臺階法在軟件編程中易于實現,加減速時間得到了有效控制。減速和加速采用同一個曲線會影響減速時間,合理利用步進電機的定位轉矩特性,可使電機快速地停止,提高電機的效率。
3 電流補償控制
常用的斬波恒流驅動方式的原理是采用電流波形補償控制技術,只不過參考電流是固定值,參考文獻和提出了改變電流參考波形的補償控制技術,在繞組供給值較小時,通過自動切換參考電流波形的方式實現增大高頻牽出轉矩。本文在研究該技術的基礎上,提出一種基于調頻調壓方式的實時電流補償控制方法。不僅提高高頻性能,在電機低速時也能迅速降低注入繞組的電流,保證低頻平穩(wěn)運行。
二相混合式步進電機給定的半步工作方式的理想參考電流波形如圖5所示,電流能達到設定值ia。但是由于繞組是感性元件,實際電流的波形如圖6所示,不是完全的方波形式,圖中的陰影部分是電流減少的部分。這種現象隨著電機運行頻率的增大變得更加明顯。當電機的頻率達到電機臨界值時,電機進入電流不可控頻段,陰影部分的面積急速劇增,電機轉矩出現明顯下降。
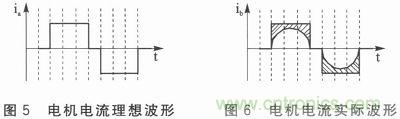
如圖7陰影部分所示,電機高頻運行時,為使電機繞組在短時間內仍能獲得足夠驅動電機運轉的能量,在原先設定的電流波形的基礎上額外增加供給電流,補償減少的部分,提高相應的牽出轉矩。低頻時,為防止電流過剩,導致低頻振蕩,實時減少電流供給,如圖8陰影部分所示。
保證電流的有效補給,f與u的變化呈現一個非線性關系模型,并與Logistic生物增長模型近似逼近。邏輯斯諦是一類非線性回歸模型,提出這個模型的初衷是為了解釋新物種在生態(tài)系統的增長變化趨勢。當一個物種遷徙到一個陌生的生態(tài)系統,而且該物種的起始總數量小于新的生態(tài)系統的最大容納量,則數量會增長,增長趨勢滿足邏輯斯諦方程。Logistic模型表達式為
式中x是自變量,y是x的函數,a、β、k是待定的常數。
物種到達一個新環(huán)境后的增長趨勢如圖9所示。從最初的起始值增長至平衡值,即式(7)中的常數a;β決定初始值的大小,β大于0時起始值落于最大值的下方,等于0時y為一條直線,小于0時起始值大于最大值a;而k是增長快慢的常數,k越大增長速度越快,且k只能為正數。
圖9:增長趨勢模型圖
電機的繞組電壓與頻率的最佳曲線關系如圖10所示。
由此得出電壓和頻率的驅動方程。
式中f為頻率,u為電壓,a、b和c為驅動系數,e為自然對數的底數。在f的增大過程中,u的變化趨勢是先緩慢,再急劇,最后慢慢趨近于a,即設定的最大驅動電壓值。
4 實驗與結論
電機選用無錫三拓二相混合式步進電機57HS5125A4,額定電流2.5 A,最高起動頻率約為200 Hz,步距角1.8°。若PWM最終信號頻率設置為500 Hz,則f=0.8×500 Hz=400 Hz。在加速至400 Hz時采用臺階緩慢升速;減速過程由20%余量的臺階實現。選取合適的b值可以確定加速時間,b取0.05,加速時間約為0.3 s,減速時間為0.05 s,加速不失步,上升快而穩(wěn),是一種比較合適的升速曲線;減速沒有過沖現象。二者形成最佳升降速控制曲線。
該設計方案已做成實物并在使用之中,測得某一相繞組電壓和頻率之間的波形變化關系,如圖11所示。頻率和電壓采用邏輯斯諦模型電壓控制方式,繞組脈沖信號的頻率越高,供電電壓也越來越高,電流實時補償,波形毛刺較小,驗證了本方案的正確性。
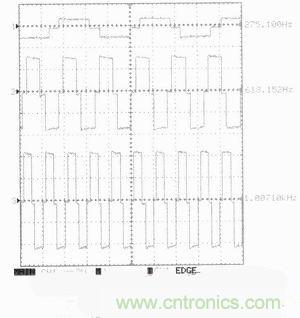
圖11:實測繞組變化圖
相關閱讀:
國內現行軌道交通安全門系統驅動電機控制方案
電機控制實時性能與效率的智能優(yōu)化方案
網友分享:基于Audrinode 的直流電機控制









