【導讀】理想的運算放大器模型具有無限的增益、帶寬、輸入阻抗和輸出導納,以及幾乎為零的輸入失調電壓和偏置電流。但在運算放大器現實的工作環境中,偏離理想狀態是正常的,比如一個直流測量系統,失調電壓的存在就不容忽視。運算放大器的失調電壓會引起直流信號輸出產生誤差,甚至減小輸出動態范圍。本文提出了一種計算失調電壓的通用方法。
運算放大器是電子電路系統設計中使用最廣泛的組件之一。盡管功能簡單,它們卻表現出復雜的行為,因為運放本身是由十幾個晶體管組成的精心制作的子電路。理想化的運放模型,即無限大的增益、帶寬、輸入阻抗和輸出導納以及零值的輸入失調電壓和偏置電流,是分析運放電路(Op Amp-based circuit)的良好一階近似。
根據運放的工作環境,可以分析它與理想行為的偏差。DC測量系統就是這樣一種環境。在這種應用中,失調電壓的存在不容忽視。它與信號處理鏈不同,在信號處理鏈中可用一個電容器輕松地濾除直流偏移。運放的失調電壓會導致直流信號的輸出誤差。另外,如果失調電壓值不可忽視,它們可減小輸出的動態范圍。各種文獻和教科書對失調電壓的存在都有描述。
本文提出了一種當電路中使用的運放具有輸入失調量e時,計算輸出失調量的通用方法。
理想運放的傳遞函數由等式y = A(V+ - V-)描述,其中y是輸出,A是增益,A→∞,V+和V-分別是運放正、負輸入端的電壓。假設實際運放輸入/輸出傳輸特性為y = A(V+ - V- + e),其中e是理想運放的差分輸入誤差,可以計算出失調量。該模型與實際運放中觀察到的結果一致:當輸入存在差異時(V+ ≠ V-),輸出為零;當V+ = V-時,實際運放產生非零輸出。 假設運放的函數模型為y = A(V+ - V- + e),其中e是輸入失調電壓,當用于負反饋配置時,我們得到:
或者,對于在負反饋配置中使用的任何運放,V+ - V- = - e(假設增益無限大)。
因此,分析理想運放電路時廣泛遵循的運放“黃金法則”需要做一些修改,以便包含表示輸入失調電壓存在的值e。
• 在采用負反饋配置運放的電路中,V- = V+ + e;
• 運放正極或負極輸入/輸出電流為零。
現在考慮圖1所示的電路拓撲結構。原理圖拓撲結構映射到圖2所示的電路,其電阻網絡分別由戴維南(Thevenin)等效電路(從端子向外看)替換為Vth+、Rth+和Vth-、Rth-。
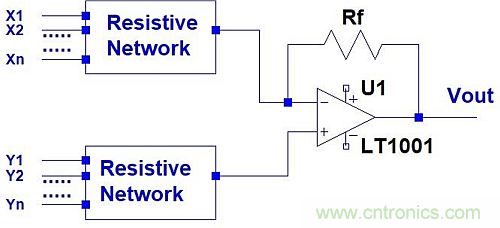
圖1:負反饋運放電路的一般拓撲結構。
運用黃金法則:
V− = V+ + e = Vth+ + e,因為V+ = Vth+。 在圖2中運放的負極端應用基爾霍夫電流定律,得出:
用Vth+、Vth-和e求解Vout,得到:
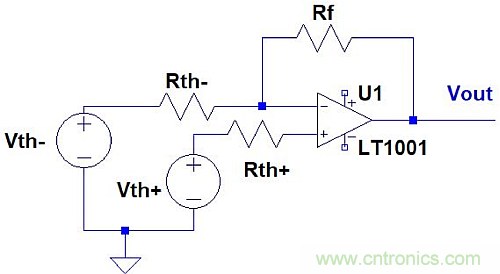
圖2:圖1所示的電路拓撲映射到該電路。
F(Vth+, Vth-, 0)僅僅是理想運放的輸出(即輸入失調電壓是零)。因此,輸出失調為:
我們將在廣泛使用的各種運放電路的輸出失調計算中應用上述導出公式。
1.差分放大器
參見圖3。在這種情況下:
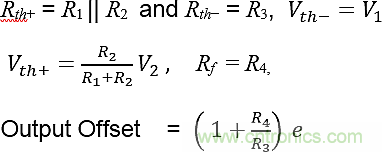
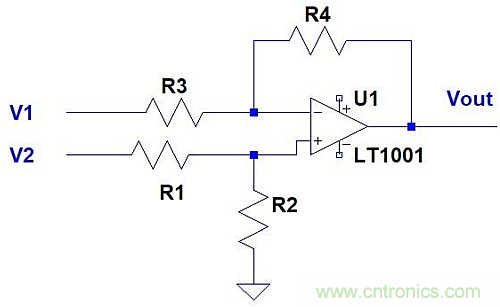
圖3:差分放大器。
1a. 同相放大器
差分放大器的一個特例,V1 = 0和R1 = 0。
2.求和放大器
見圖4。
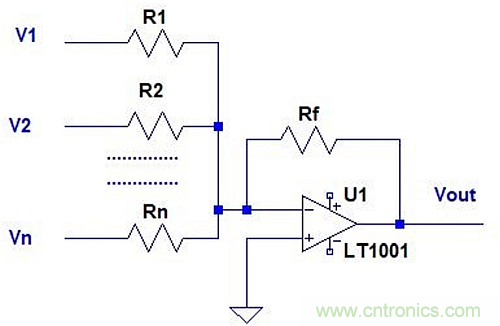
圖4:求和放大器。
在這種情況下,Rth- = R1 || R2 || R3 ……….|| Rn,因此:
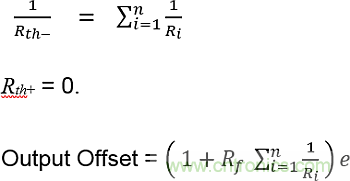
2a. 反相放大器
求和放大器特例,n = 1。
2b. 二進制加權數模轉換器
上面顯示的求和放大器特例,其中:

3. R-2R梯形數模轉換器
眾所周知,R-2R梯形的等效輸出電阻是R,與梯形的長度無關。圖5和圖6顯示了兩種實現方式。在圖5中:
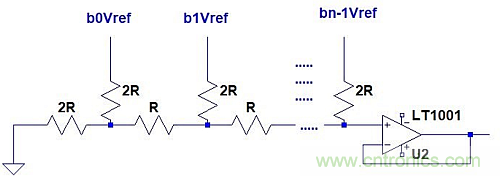
圖5:具有緩沖輸出的R-2R梯形數模轉換器。
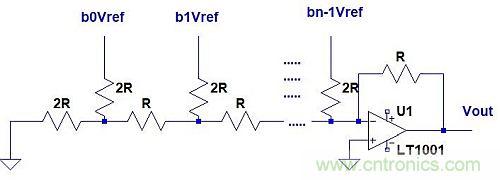
圖6:帶反相輸出的R-2R梯形數模轉換器。
在圖6中:
當n值較小,與圖6中的R-2R DAC相比,加權二進制DAC產生的輸出失調更小。
考慮偏置電流
本節的輸出失調計算考慮了偏置電流。假設流出正、負端子的偏置電流分別為IB+和IB-(+值為輸出電流)。參考圖2。
在運放負端應用基爾霍夫電流定律,得出:
用Vth+、Vth-、e、IB+、IB-求解Vout,得到:
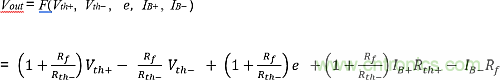
F(Vth+, Vth-, 0, 0, 0)為理想運放的輸出。因此,輸出失調量由下式給出:
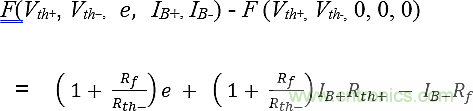
計算出上述每一種情況的Rth+和Rth-后,總失調量的計算就是簡單地將適當的值代入上述等式中。
本文轉載自電子技術設計。
推薦閱讀:








