【導讀】RC濾波器使用等效結構,但是我們有一個電容器代替R 2。首先,我們用電容器的電抗(X C)代替R 2(在分子中)。接下來,我們需要計算總阻抗的大小并將其放在分母中。
6、計算過濾器響應
我們可以通過使用典型分壓器計算的頻率相關版本來計算低通濾波器的理論行為。電阻分壓器的輸出表示如下:
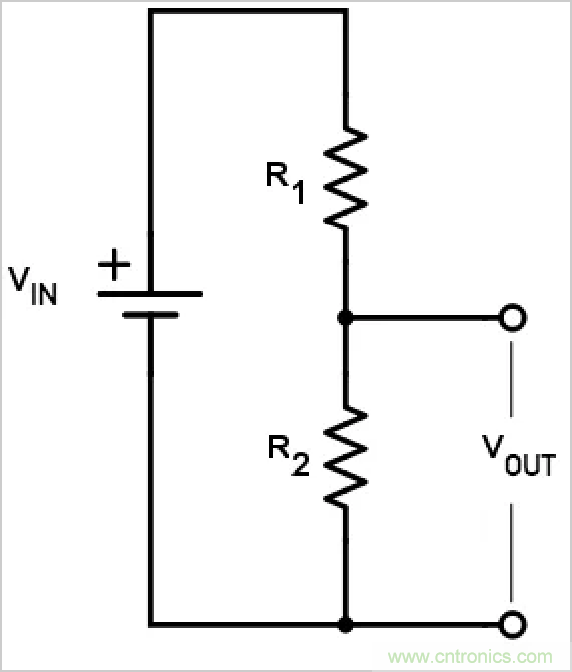
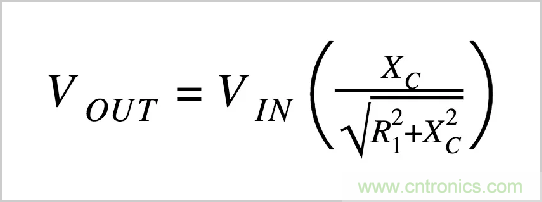
RC濾波器使用等效結構,但是我們有一個電容器代替R 2。首先,我們用電容器的電抗(X C)代替R 2(在分子中)。接下來,我們需要計算總阻抗的大小并將其放在分母中。因此,我們有:
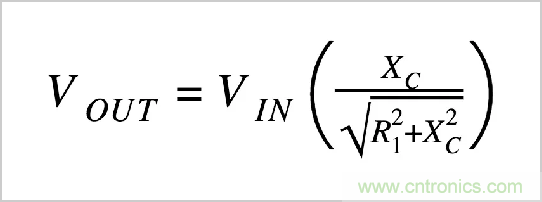
電容器的電抗表示與電流的相反量,但與電阻不同,相反量取決于通過電容器的信號頻率。因此,我們必須計算特定頻率的電抗,我們用于此的等式如下:
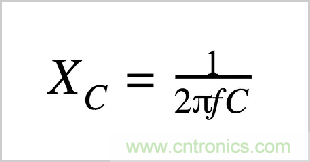
在上面的設計實例中,R≈160Ω且C = 10nF。我們假設V IN的幅度是1 V, 這樣我們就可以簡單地從計算中去掉V IN。首先讓我們以正弦波頻率計算VOUT的幅度:
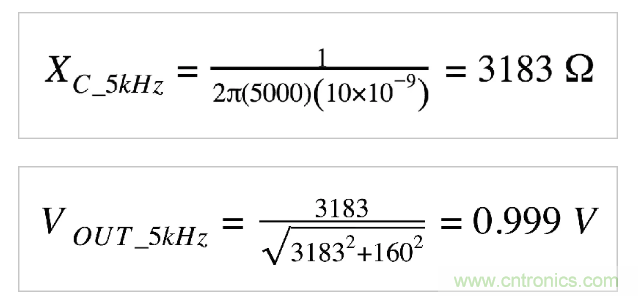
正弦波的幅度基本不變。這很好,因為我們的目的是在抑制噪音的同時保持正弦波。這個結果并不令人驚訝,因為我們選擇的截止頻率(100 kHz) 遠高于正弦波頻率(5 kHz)。
現在讓我們看看濾波器如何成功衰減噪聲分量。
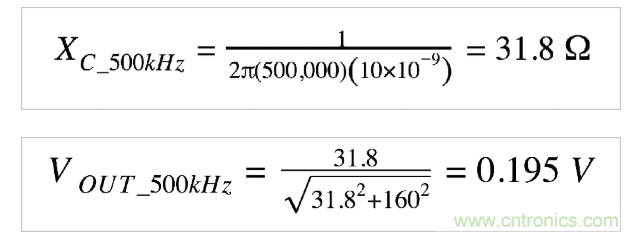
噪聲幅度僅為其原始值的約20%。
7、可視化過濾器響應
評估濾波器對信號影響的最方便方法是檢查濾波器頻率響應的圖。這些圖形通常稱為波德圖,在垂直軸上具有幅度(以分貝為單位),在水平軸上具有頻率; 水平軸通常具有指數標度,使得1Hz和10Hz之間的物理距離與10Hz和100Hz之間,100Hz和1kHz之間的物理距離相同。這種表示方法使我們能夠快速準確地評估濾波器在很大頻率范圍內的作用。
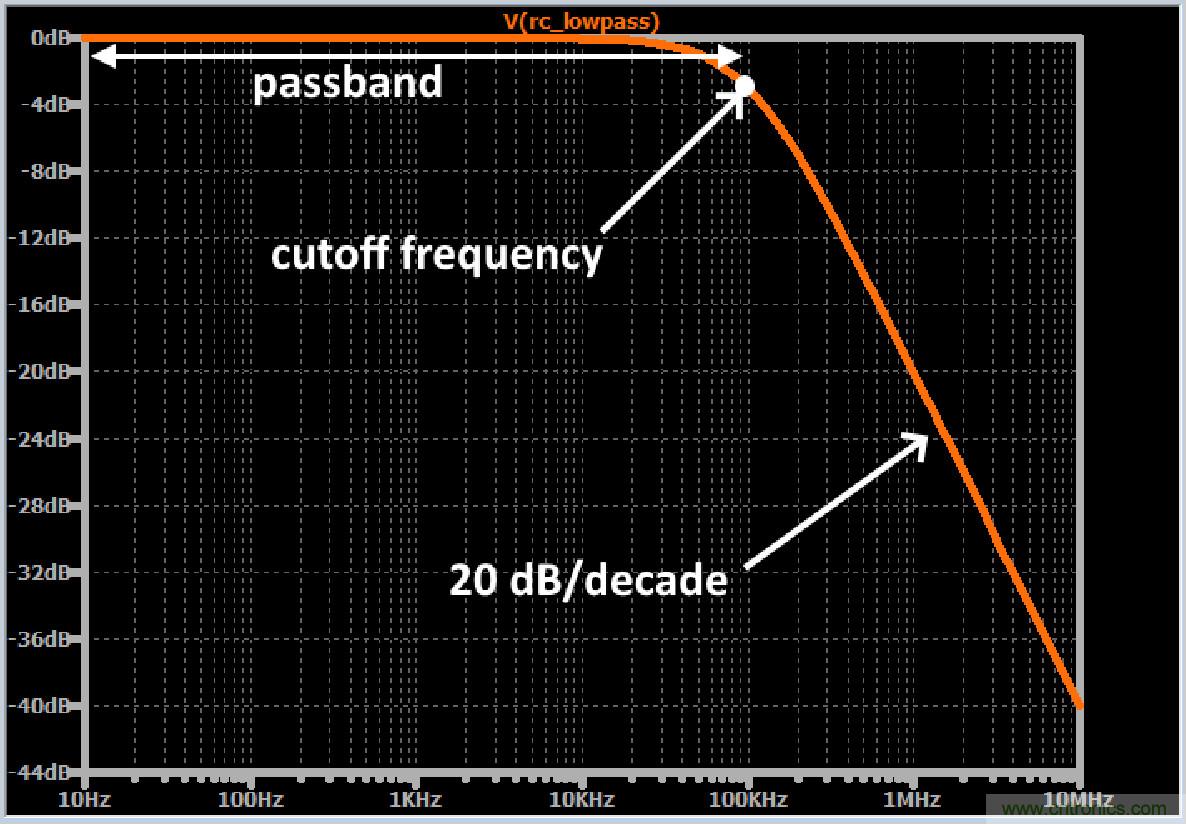
頻率響應圖的一個例子
曲線上的每個點表示如果輸入信號的幅度為1 V且頻率等于水平軸上的相應值,則輸出信號將具有的幅度。例如,當輸入頻率為1 MHz時,輸出幅度(假設輸入幅度為1 V)將為0.1 V(因為-20 dB對應于十倍減少因子)。
通帶中的曲線幾乎完全平坦,然后隨著輸入頻率接近截止頻率,它開始下降得更快。最終,衰減的變化率穩定在20 dB / decade。即,輸入頻率每增加十倍,輸出信號的幅度降低20 dB。
8、評估低通濾波器性能
如果我們仔細繪制我們在本文前面設計的濾波器的頻率響應,我們將看到5 kHz時的幅度響應基本上是0 dB(即幾乎為零衰減),500 kHz時的幅度響應約為-14 dB(對應于0.2的增益)。這些值與我們在上一節中執行的計算結果一致。
由于RC濾波器總是從通帶到阻帶逐漸過渡,并且因為衰減永遠不會達到無窮大,我們無法設計出“完美”的濾波器 - 即對正弦波完全沒有影響并完全消除噪聲的濾波器。相反,我們總是需要權衡。如果我們將截止頻率移近5 kHz, 我們將有更多的噪聲衰減,但我們想要發送到揚聲器的正弦波衰減更多。如果我們將截止頻率移近500 kHz,我們在正弦波頻率下的衰減會減少,但噪聲頻率下的衰減也會減少。
9、低通濾波器相移
到目前為止,我們已經討論了濾波器修改信號中各種頻率分量幅度的方式。然而,除了幅度效應之外,電抗性電路元件總是引入相移。
相位的概念是指周期內特定時刻的周期信號的值。因此,當我們說電路引起相移時,我們的意思是它會在輸入信號和輸出信號之間產生不對準:輸入和輸出信號不再在同一時刻開始和結束它們的周期。相移值(例如45°或90°)表示已創建多少未對準。
電路中的每個電抗元件都會引入90°的相移,但這種相移不會同時發生。輸出信號的相位與輸出信號的幅度一樣,隨著輸入頻率的增加而逐漸變化。在RC低通濾波器中,我們有一個電抗元件(電容器),因此電路最終會引入90°的相移。
與幅度響應一樣,通過檢查水平軸表示指數頻率的曲線圖,可以最容易地評估相位響應。下面描述了一般情況,然后我們可以通過檢查繪圖來填寫詳細信息。
相移最初為0°。
它逐漸增加,直到它在截止頻率達到45°; 在這部分響應期間,變化率正在增加。
在截止頻率之后,相移繼續增加,但變化率正在降低。
隨著相移漸近接近90°,變化率變得非常小。
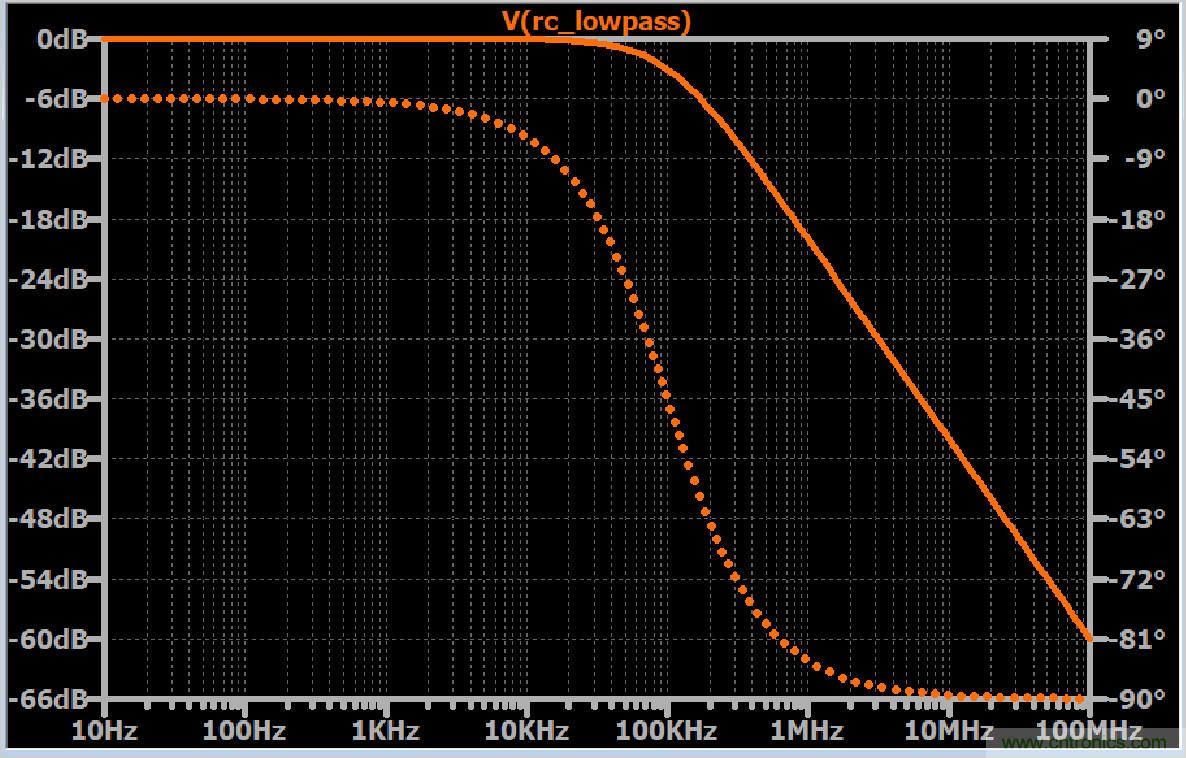
實線是幅度響應,虛線是相位響應。截止頻率為100 kHz。注意,截止頻率下的相移為45°
10、二階低通濾波器
到目前為止,我們假設RC低通濾波器由一個電阻器和一個電容器組成。此配置是一階過濾器。
無源濾波器的“次序”由電路中存在的電抗元件(即電容器或電感器)的數量決定。高階濾波器具有更多的無源器件,這導致更多的相移和更陡的衰減。通過向濾波器添加一個電抗元件 ,例如,從一階到二階或二階到三階,最大斜率就會增加20 dB /十倍。更陡峭的斜率轉換為從低衰減到高衰減的更快速轉換,所以當一階濾波器不具有將期望頻率分量與噪聲分量分離的寬頻帶時,用多階濾波器可以實現目的。
11、總結
總結如下:
所有電信號都包含所需頻率分量和不需要的頻率分量的混合。不期望的頻率分量通常由噪聲和干擾引起,并且在某些情況下它們將對系統的性能產生負面影響。
濾波器是以不同方式對信號頻譜的不同部分作出反應的電路。低通濾波器旨在傳遞低頻分量并阻止高頻分量。
低通濾波器的截止頻率表示濾波器從低衰減轉變為顯著衰減的頻率區域。
RC低通濾波器的輸出電壓可以通過將電路視為由(頻率無關)電阻和(頻率相關)電抗組成的分壓器來計算。
幅度(以dB為單位,在垂直軸上)與頻率(以赫茲為單位,在水平軸上)的曲線圖是檢查濾波器理論行為的方便有效的方法。我們還可以使用相位與指數頻率的關系圖來確定將應用于輸入信號的相移量。
二階濾波器提供更陡峭的衰減; 當信號不能在所需頻率分量和不需要的頻率分量之間提供寬帶分離時,這種二階響應是有用的。
免責聲明:本文為轉載文章,轉載此文目的在于傳遞更多信息,版權歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權問題,請聯系小編進行處理。








