【導讀】永磁同步電機 (PMSM) 由于其高效率、高功率密度和出色的機械動力性能而廣泛應用于工業領域。PMSM通常采用磁場定向控制 (FOC,也稱矢量控制)來驅動,以提升其動態響應并能 充分利用電機潛力。PMSM 矢量控制包含電流環,速度環和位置環。為了實現最佳性能的控制設計,工程師需要精準的電機參數為 PMSM 控制系統建立適當的機械和電氣數學模型。
數據手冊并不總是可以獲得,即使有,通常也不會涵蓋每臺電機面對的工作條件。本文將介紹一種識別 PMSM 參數的簡單方法,它利用 MPS的智能電機控制模塊解決了這個難題。這種智能電機基于帶遺忘因子的遞歸最小二乘 (RLS) 算法,可以實時修改和監測 PMSM參數的變化。
PMSM的磁場定向控制(FOC)
FOC 的基本思想是能夠分別控制磁通量和扭矩,類似于控制直流電機的方式。根據 Clarke 和 Park 變換,同步旋轉 Q-D 坐標系下的 PMSM 模型可以使用等式(1)、等式(2)、等式(3)和等式(4)來計算: $$v_{QS}=r_S+ω_Rλ_{DS}+ρλ_{QS}$$
$$v_{DS}=r_{S}-ω_rλ_{QS}+ρλ_{DS}$$
$$λ_{QS}=L_Si_{QS}+L_Mi_{QR}$$
$$λ_{DS}=L_Si_{DS}+L_M i_{DR}$$ 其中下標 Q 和 D 分別表示 Q 軸和 D 軸變量, LS為電機自感,LM為電機互感。
為了進一步簡化控制,轉子磁通應在 D 軸上對齊,而 Q 軸上的轉子磁通為零。Q 軸和 D 軸的磁通量可以分別用等式 (5) 和等式 (6)來估算:
$$λ_{QS}=L_Si_{QS}$$
$$λ_{DS}=L_Si_{DS}+λ_M^{''''''''}$$ 電磁扭矩可以用公式(7)來計算: $$T_E= frac {3} {2} frac {P}{2} (λ''''''''_{M}i_{QS} + (L_{D} - L_{Q}) i_{DS}i_{QS}) $$
遵循上述方程的轉換步驟,磁通量可以直接由 D 軸電流控制。采用恒定的IDS,可以通過調節 Q 軸電流直接控制扭矩 (TE)。 如果IDS= 0,則電磁扭矩與IQS成正比。 通過上述推導,我們可以得出PMSM的FOC原理圖(見圖 1)。
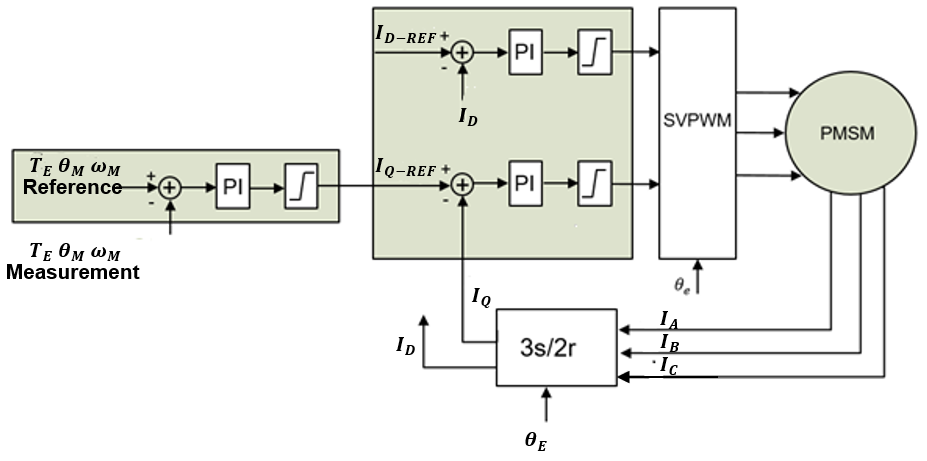
圖 1:PMSM 矢量控制原理圖
外環參考值可以是所需的扭矩、電機速度或特定的軸位置。將外環參考值與測量值進行比較,并將誤差饋入控制器(通常為 PI 控制器)以生成扭矩電流參考值 (IQ-REF)。
D 軸電流參考值 (ID-REF) 根據磁通量要求來設置。電流調節器/控制器的輸出(VQ-REF和VD-REF)為空間矢量 PWM (SVPWM) 的輸入。SVPWM 模塊為逆變器生成柵極信號以驅動 PMSM。
為實現 PMSM 伺服電機所需的動態性能,MPS的智能電機控制模塊可以提供參數自整定功能,而且可以根據給定的帶寬要求自動調整每個 PI 控制器。
對于電流環,開環傳遞函數可以用公式(8)來估算: $$G = frac{KPS+KI} {S} frac {1}{L_{S}S + r_S}$$
對于給定電流帶寬S =jω,可以根據定子電阻和電感反向計算出PMSM 控制參數(KP 和 KI)。
與電流環類似,外環(機械環)開環函數可以用公式(9)計算: $$G = frac{KPS+K1} {S} frac {kt}{JS + B}$$
其中 kt 為電機扭矩常數,J 為慣量,B 為摩擦系數。
從等式 (9) 可知,已知電機扭矩常數 (kt)、慣量 (J) 和摩擦系數 (B),可以計算出外環的控制參數。
遞歸最小二乘算法
遞歸最小二乘算法 (RLS) 是最小二乘 (LS) 回歸算法的遞歸應用,從每次迭代中獲取新數據以修改系統先前的估值。
系統輸出 (y(t)) 可以用公式 (10) 來計算: $$y(t)=?^T (t)θ(t)$$ 其中 ? 是系統輸入矩陣,θ 是 PMSM 系統參數。
用$hat θ$ (這個符號請copy 英文原文字母) 表示估算的系統參數。目標函數,或旨在最小化或最大化的項,可以用等式 (11) 來估算:
$$J(θ,t)= frac {1}{2} ∑_{i=1}^t(y(i)-phi^T (i) hatθ (i)) $$ P 和 L 的新矩陣可以分別用等式 (12) 和等式 (13) 來計算: $$P^{-1}
(t)=∑_{i=1}^tphi(i)phi^T(i)$$ $$L(t)=P(t)phi(t)$$
遞歸最小二乘參數識別方案通過等式(14)、等式(15)、等式(16)、等式(17)和等式(18)估算: $$?(t)=(y(t)-phi^T (t)) hatθ (t-1)$$
$$L(t)=P(t-1)phi(t) (I+phi^T (t)P(t-1)phi(t))^{-1}$$
$$P(t)=(I-L(t)phi^T (t))P(t-1)$$
$$hatθ(t)=hatθ (t-1)+L(t)?(t)$$
$$t=t+1$$
在算法中添加一個遺忘因子能夠使方案得以處理時變系統。根據數據的新舊,賦予遺忘因子數據以一定的權重。因為舊數據對當前迭代的影響較小,所以給最新數據賦予算法的最大權重。遺忘因子 (λ) 的取值范圍在 [0,1] 之間。新的目標函數可以用等式(19)來估算:
$$J(θ,t)=frac {1}{2} ∑_{i=1}^tλ^{t-i} (y(i)-phi^T (i)hat θ (i)) $$
使用方程 (19) 中的新目標函數,第 n 個舊數據的權重為 λn。帶遺忘因子的遞歸最小二乘方案可以通過等式 (20)、等式 (21)、等式 (22)、等式 (23) 和等式 (24) 來計算:
$$ ?(t)=(y(t)-phi^T (t)) hatθ (t-1)$$
$$L(t)=P(t-1)phi(t) (λI+phi^T (t)P(t-1)phi(t))^{-1}$$
$$P(t)= frac {1}{λ}(I-L(t) phi^T (t))P(t-1)$$
$$hatθ (t)=hatθ (t-1)+L(t)?(t)$$
$$t=t+1$$
實驗結果
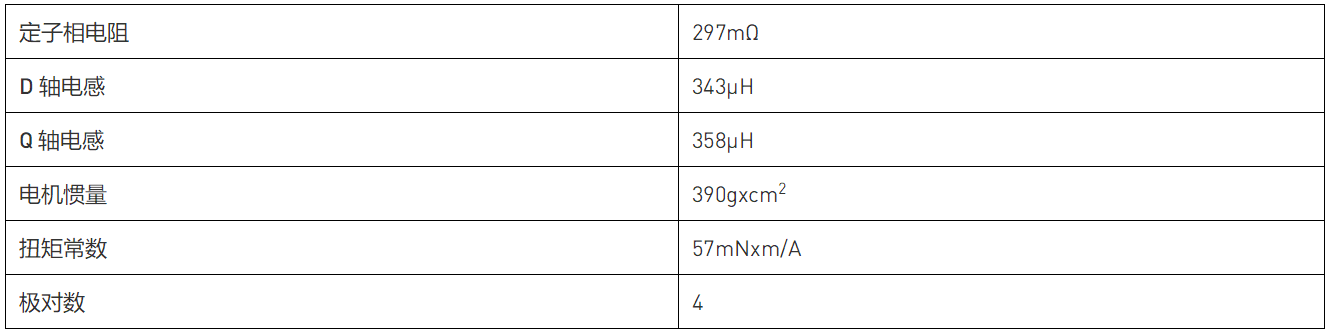
MPS’s MMP757188-36 是一款已經過驗證的 智能電機。表 1 列出了其數據手冊中的電機參數。
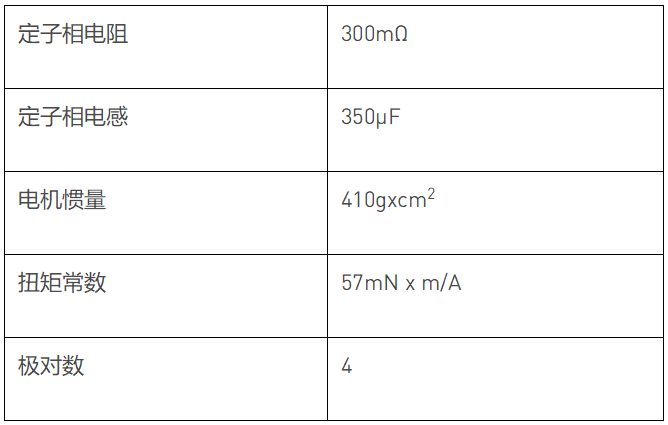

圖 2:MPS 智能電機(MMP757188-36)
將以下電機參數的初始起點設置為[0 0 0 0 0]T: 相電阻(RS),Q軸電感(LQ),D軸電感(LD),扭矩常數(kt), 和電機軸慣量(J).
對于 RLS 算法,初始 P 矩陣設置為P = 10000 x I5 x 5,遺忘因子設置為 λ = 0.99.
將啟動條件應用到 MPS 智能電機控制模塊,執行 RLS 電機參數算法。圖 3、圖 4、圖 5、圖 6 和圖 7 顯示了其硬件實驗結果。
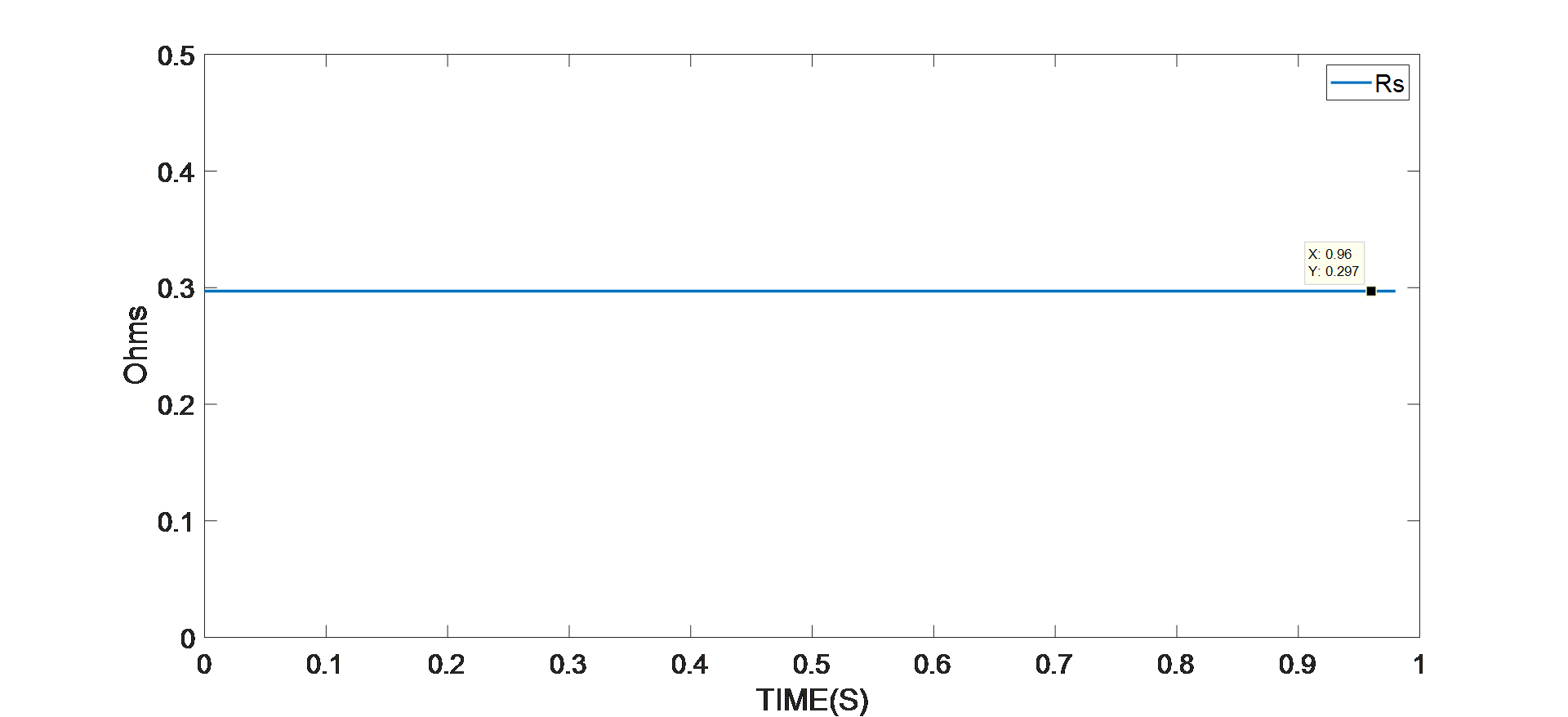
圖 3:電阻識別的實驗結果
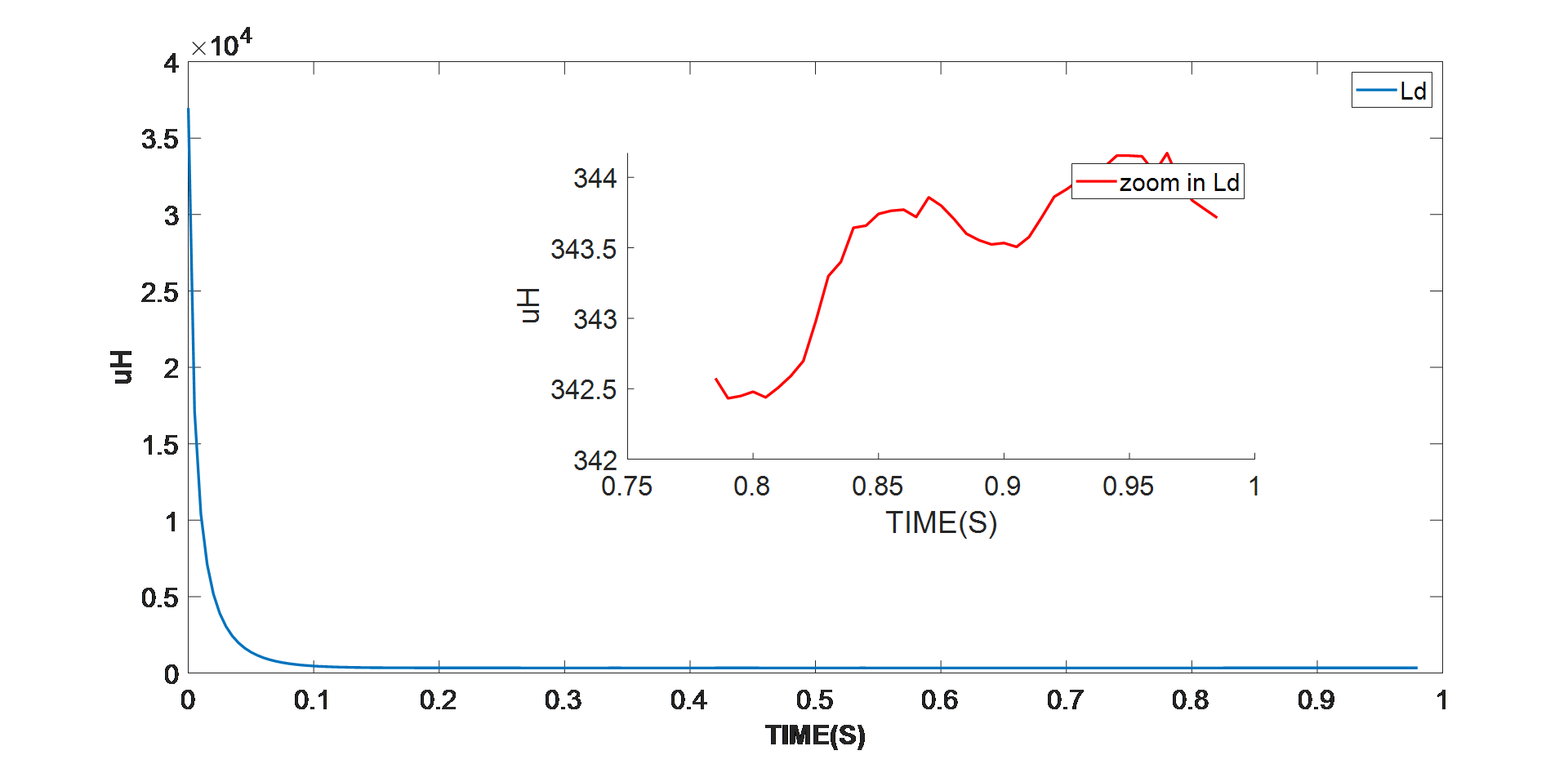
圖 4:D 軸電阻識別的實驗結果
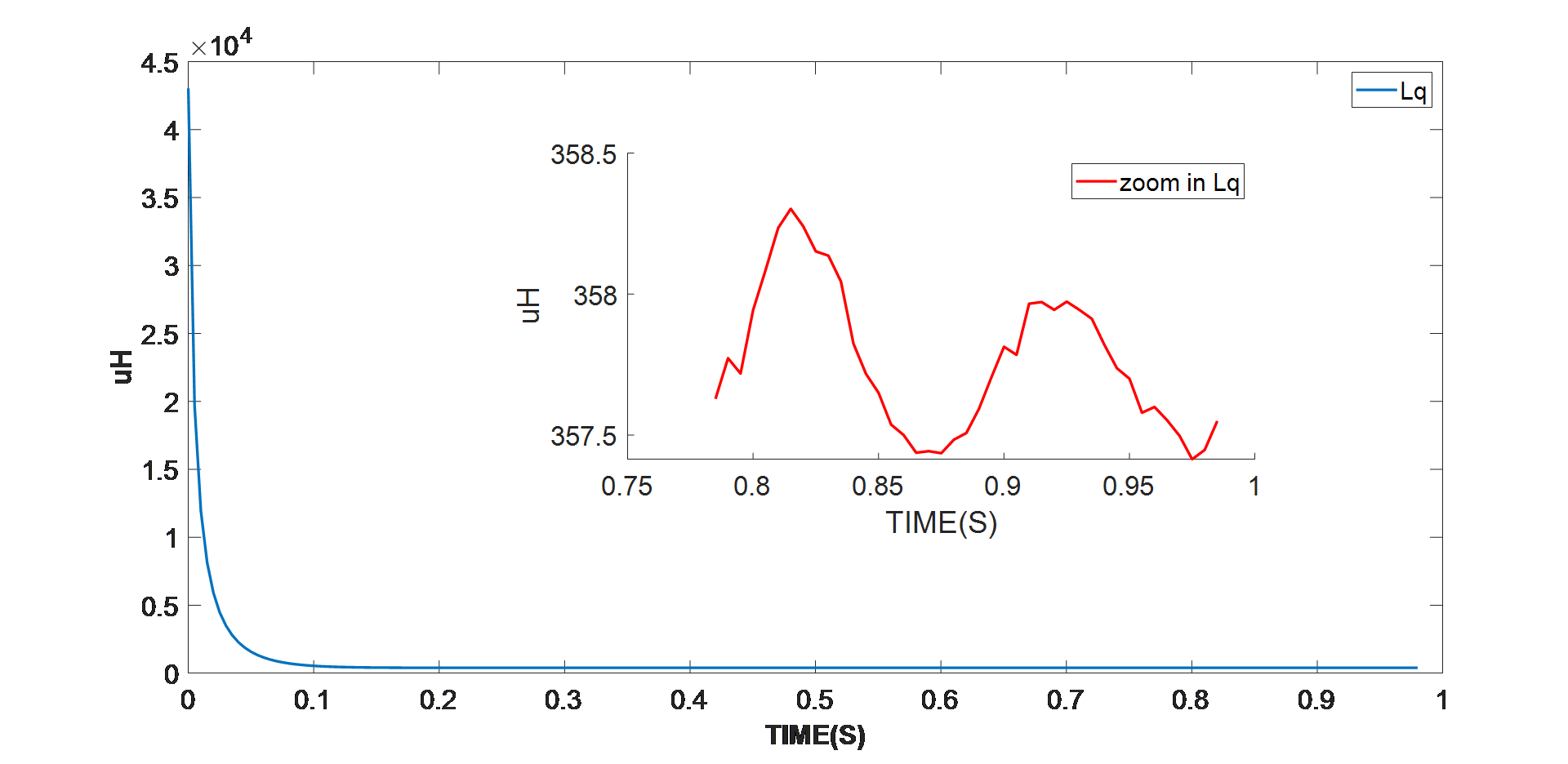
圖 5:Q 軸電阻識別的實驗結果
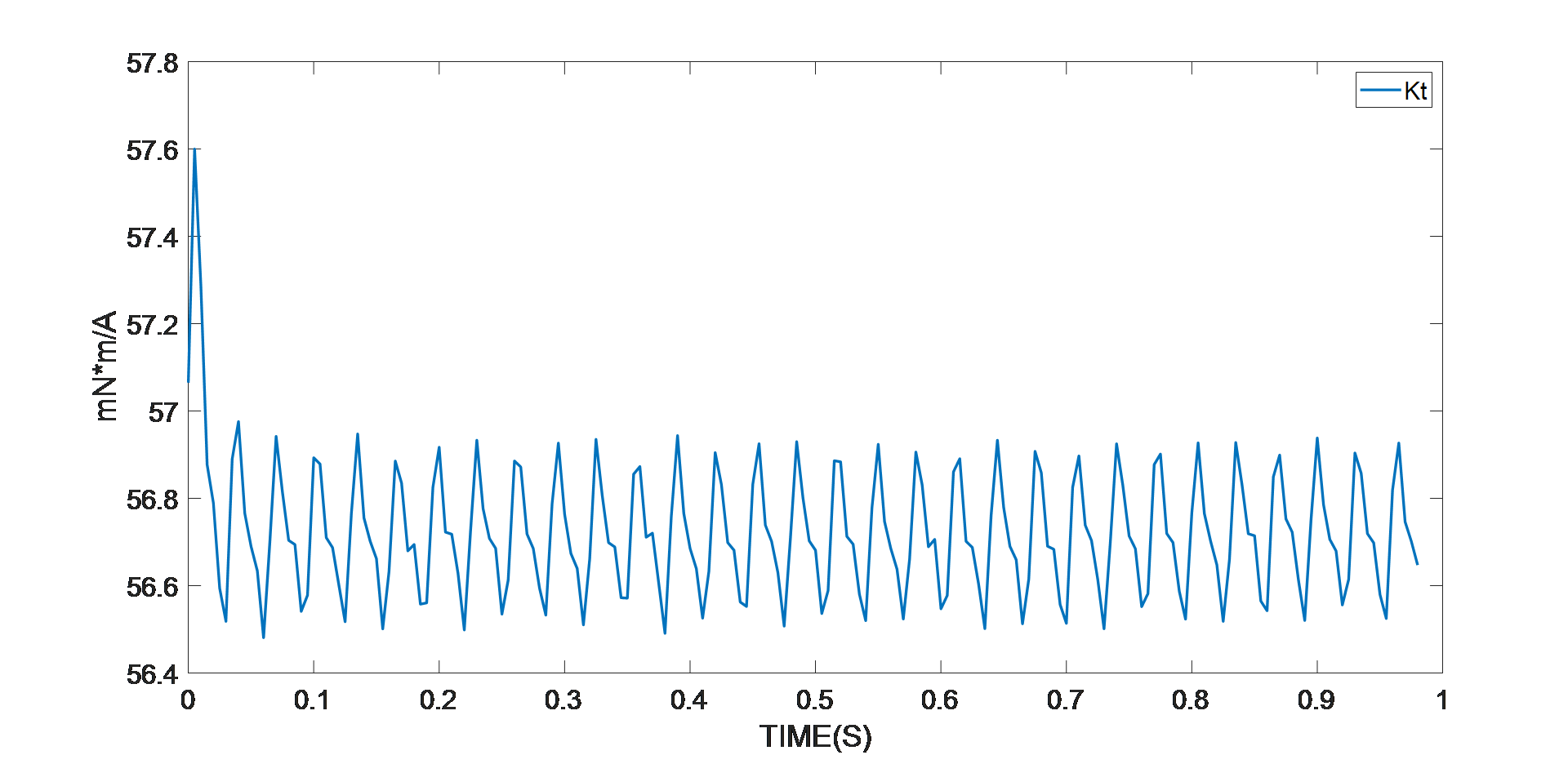
圖 6:扭矩常數識別的實驗結果
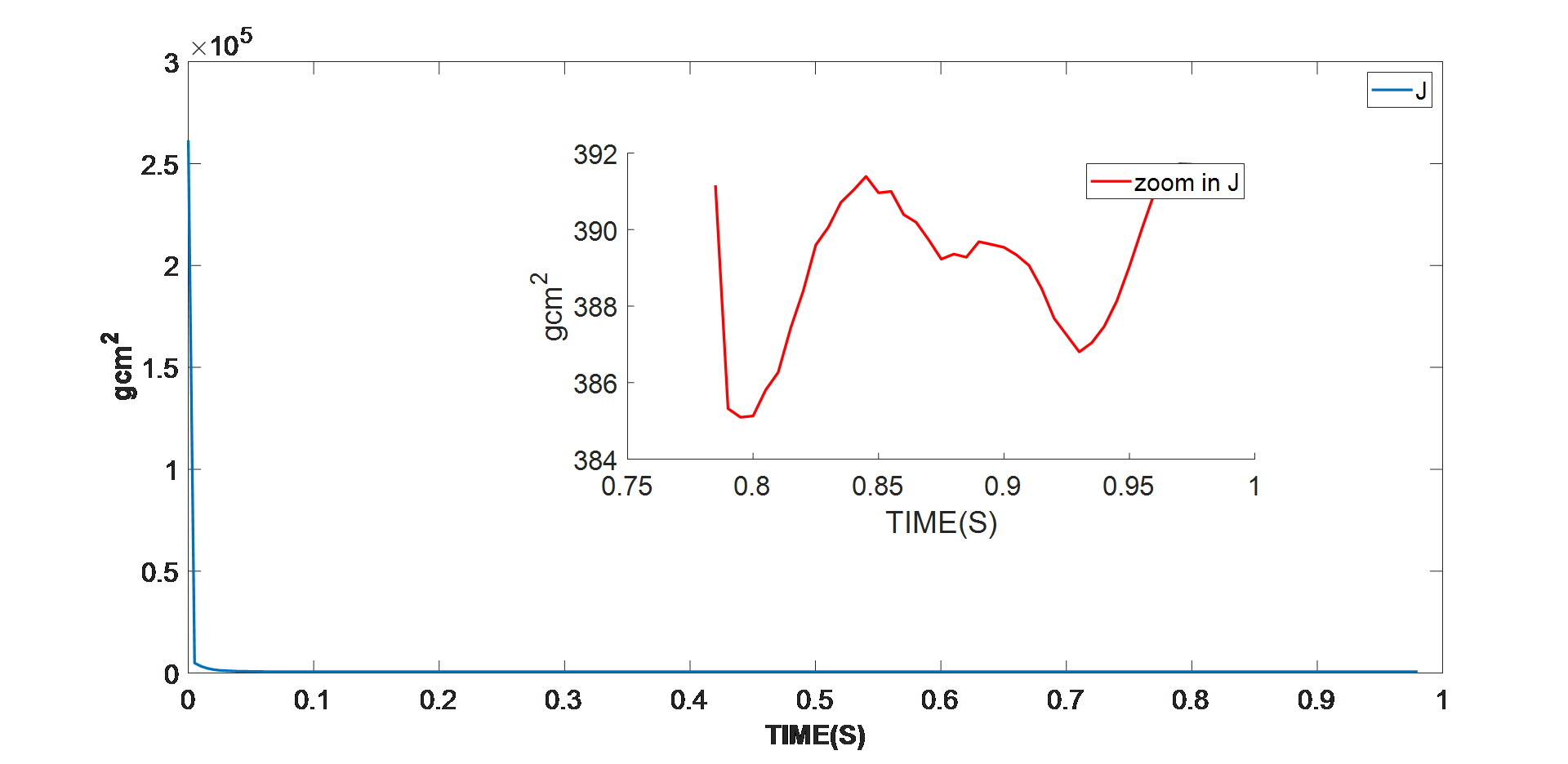
圖 7:軸慣量識別的實驗結果
智能電機控制模塊(本例中為 MMP757188-36)檢測參數識別算法是否已進入穩定階段。如上圖所示,在算法進入穩定狀態之后,采用最終值,即平均電機參數值。
控制環自整定
如前文所述,電機參數會影響 PMSM 的 FOC 控制參數。為幫助工程師實現所需的電機性能,MPS 控制套件配備了智能電機控制模塊,該模塊使用公式 (8) 和公式 (9) 中得到的系統傳遞函數自動調整控制參數。如果已知電機參數,工程師只需通過 MPS eMotion GUI 為每個環路輸入所需的帶寬。上位機計算電機的控制參數,然后將控制參數反饋給智能電機以確保其性能。
PMSM 的控制傳遞函數高度依賴電機參數。如果電機參數不正確,電機將無法有效運行。在下面關于改變軸慣量 (J) 的示例中,我們將進一步討論這個問題。
PMSM 通常被用作高性能伺服電機。它們的工作條件視情況而異。工程師可能有準確的電機參數數據手冊,也有可能需要手動測量電機參數。一旦將電機置于復雜的機械系統中,就很難再確定軸慣量。
MPS’s MMP757188-36可用于驅動旋轉盤(見圖 8)。旋轉盤的軸慣量從410 gxcm2增加到 7100 gxcm2。FOC設計為位置帶寬是20Hz,速度帶寬是200Hz,電流帶寬是2000Hz。

圖8:智能電機驅動旋轉盤
如果使用的電機參數來自設備的數據手冊,自動整定算法會采用預期的環路帶寬來設計控制環,但由于數據手冊僅提供空載慣量,因此電機參數會出錯。位置參考是斜率為 10rad/s 的斜坡參考。圖 9 表明,當位置環失控時,位置反饋將有較大的振蕩。
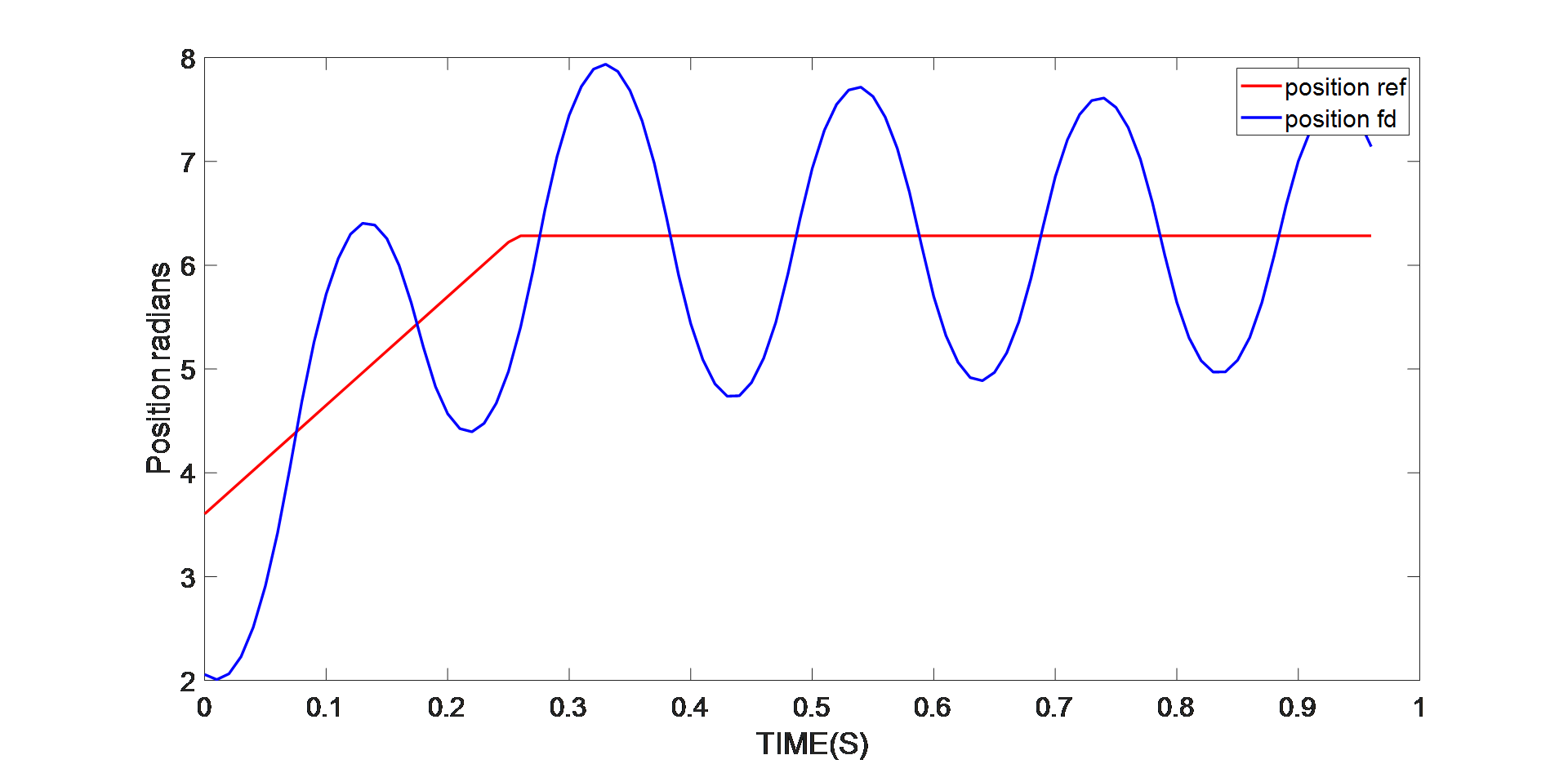
圖 9:原始 J 值的位置控制性能
采用MPS的智能電機控制模塊,運行參數識別算法。電機參數將根據電機當前工作條件更新,而自整定算法則能幫助工程師根據當前條件下的電機參數調整控制環路。電機使用相同的位置參考,位置反饋以 0.03% 左右的穩定誤差追蹤參考值(見圖 10)。
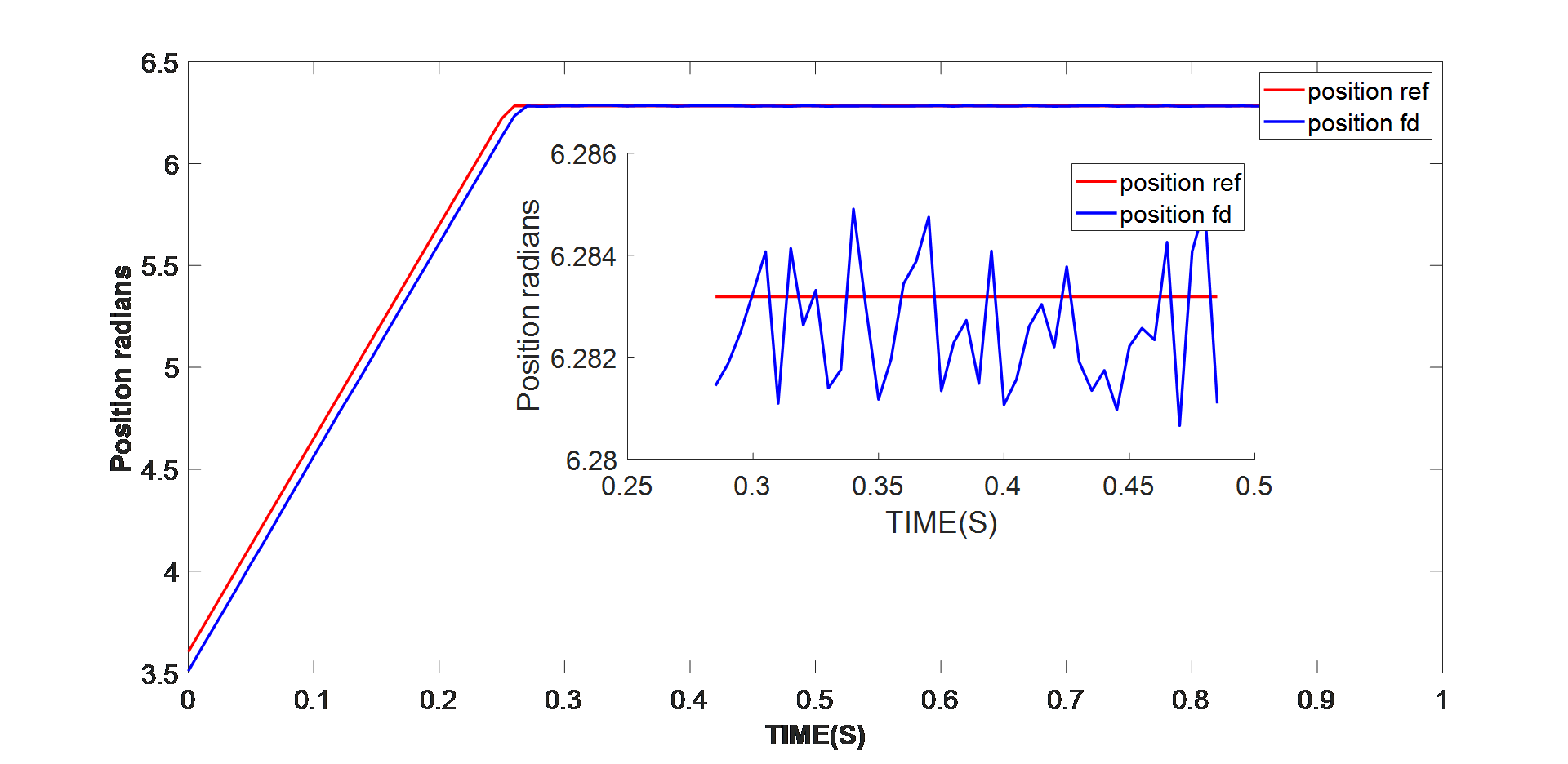
圖 10:更新 J 值的位置控制性能
結論
本文介紹了如何利用MPS智能電機控制模塊實現基于 RLS 的PMSM電機參數識別解決方案,并采用MPS 的 MMP757188-36在硬件實時測試中驗證了其性能。文中還給出了具有不同慣量值的位置控制示例,用以說明參數識別的重要性。另外,由于PMSM FOC 取決于多個電機參數,本文還證明了其他參數對控制環路的影響。
來源:MPS
免責聲明:本文為轉載文章,轉載此文目的在于傳遞更多信息,版權歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權問題,請聯系小編進行處理。
推薦閱讀:








