【導讀】本設計實例展示了一種用于綜合異步選通電路的數學方法,這種電路可以在不改變脈沖寬度的條件下,從時鐘信號中選通一個精確的脈沖串。這種電路被稱為量化器。到底如何設計的呢?
要想從一個連續的時鐘源選通一個完整的時鐘脈沖序列而又不改變脈沖的持續時間和數量,不是一件容易的事情。在大多數情況下,簡單的與門會有問題,見圖1。
只要異步選通信號E是高電平,時鐘脈沖就會通過與門。哪怕丟失或失真一個脈沖都會很關鍵,那么簡單的與門就不合適了—由于時鐘和E之間缺少同步,脈沖串中的第一個和最后一個脈沖經常會失真(比正常脈沖短)。
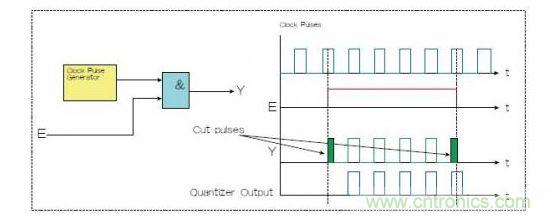
圖1:兩種選通脈沖串的方法,一種是使用選通信號E和與門(Y輸出),一種是量化器(藍色)。
本設計實例展示了一種用于綜合異步選通電路的數學方法,這種電路可以在不改變脈沖寬度的條件下,從時鐘信號中選通一個精確的脈沖串。這種電路被稱為量化器。
根據量化器的工作原理做一個狀態轉換表(圖2)。
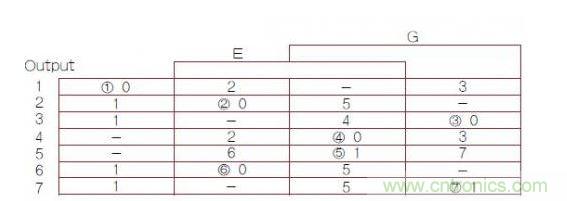
圖2:異步有限狀態機(FSM)轉換主表,其中1,2,3,4,5,6,7帶圈的數字是穩定FSM狀態號(G是時鐘輸入)。
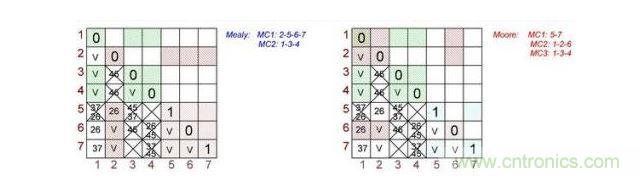
圖3:根據Mealy(左)和Moore(右)狀態機做出的最終表格對。
借助圖2并根據Mealy和Moore狀態機可以做出最終的表格對(圖3)。圖中:
MC1:2-5-6-7和MC2:1-3-4是最大兼容集(根據Mealy狀態機);
MC1:5-7、MC2:1-2-6和MC3:1-3-4是最大兼容集(根據Moore狀態機)。
從圖3可以看到,Moore狀態機的總覆蓋率要求更大數量的最大兼容子集,也就是更糟糕。另一方面,第一個狀態可以是MC2集和MC3集的一個部分,它代表了用于額外電路優化的機會。但無需進一步考慮這個問題。
現在就很容易畫出壓縮的狀態轉換表,并為Z編碼的內存單元和輸出選通信號Y畫出卡諾-維奇圖(圖4)。

圖4:卡諾-維奇圖
根據卡諾-維奇圖,為綜合出來的電路寫下邏輯公式:
從這個公式可以看出,其中針對z+的最小項[E●z]不是多余的。它在最小項[G●E]和[G●z]之間扮演著反競爭橋的重要角色,可以消除G的所有邊沿處的連續競爭。
式中:E=異步選通信號的反向輸入;
G=時鐘;
Y=量化器輸出。
還可以增加一些額外的功能,比如FLAG.當FLAG是低電平時,脈沖串中的第一個脈沖不會被剪切掉,而是合并進脈沖串并且不會影響其寬度。當FLAG是高電平時,第一個脈沖被切掉,并排除在脈沖串以外。FLAG狀態應保持不變直到下一個選通脈沖,因此設備有足夠的時間來讀取它,并用于進一步處理。








