【導讀】超外差原理是,任何頻率的輸入信號都與“本地振蕩器”的頻率“混合”,在稱為IF的“中頻”產生新的信號。本設計實例將介紹一種混頻安排,其中本地振蕩器以輸入信號的頻率運行,產生零赫的IF。
超外差接收機中使用的縮寫詞“IF”代表“中頻”,所以對于一個追求語言純粹的人,本文標題中出現了“頻率頻率”的并列就顯得荒謬。但是我決定不在意。談論一款中頻器件或電路或系統或其它任何東西都太簡單了,所以我要懇請你的寬容。
超外差原理是,任何頻率的輸入信號都與“本地振蕩器”的頻率“混合”,在我們稱為IF的“中頻”產生新的信號。在典型的AM收音機中,IF是455kHz;而在典型的FM收音機中,IF是10.7MHz。在這兩種情況下,本地振蕩器都以輸入信號的頻率運行,但由IF移頻。如果你在紐約市收聽WINS的AM電臺,選臺到1010kHz,則本地振蕩器將以1465kHz的頻率工作。
但這里我們將看到一種混頻安排,其中本地振蕩器以輸入信號的頻率運行,產生零赫的IF,正如標題所說。
下圖是用于超外差接收的零頻率IF級,只要其頻率wm = 2×pi×fm足夠接近第二本地振蕩器頻率wc= 2×pi×fc,輸入#1就被傳遞到輸出。輸入頻率有多接近必須借助一對低通濾波器來設置。兩個低通濾波器的截止頻率越低,選擇范圍越窄。
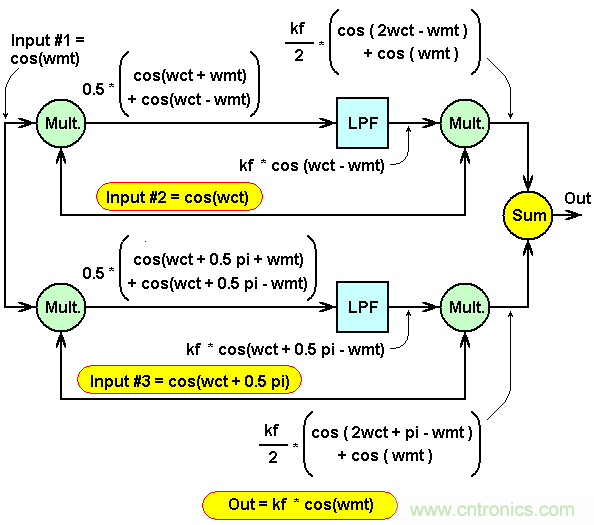
圖1:零頻率IF和公式,首次考查。
理想的乘法器是我們的混頻器。其操作基于三角函數公式:cos a x cos b = ½ x (cos (a+b) + cos (a-b)) ,如圖1所示。
但是,可以用另一種方式應用這種代數關系。我們可以用“a”代表“wc”,“b”代表“wm”,或者反過來,都沒關系。
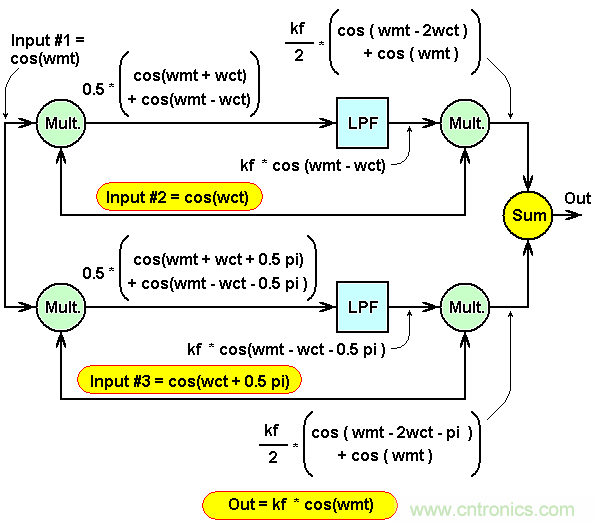
圖2:零頻率IF和公式,第二次考查。
在這種情況下,我們使用等價三角函數公式:cos b x cos a = ½(cos (b+a) + cos (b-a))。
這種差別并沒產生什么不同,圖1和圖2的最終結果相同。采用 SPICE的零頻率IF仿真如圖3所示。
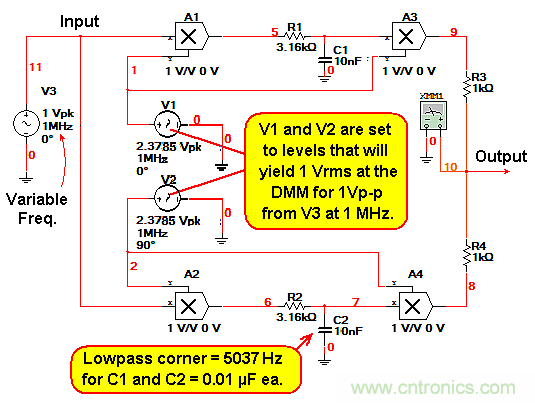
圖3:采用 5kHz低通濾波器零頻率IF仿真。
...或更窄的帶通,像圖4那樣。
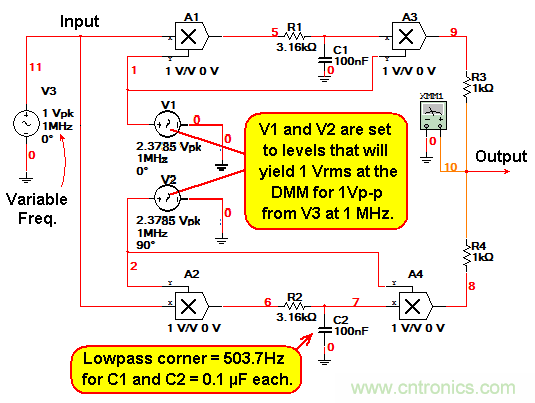
圖4:采用約500Hz低通濾波器的零頻率IF仿真。
整個帶通是低通濾波器截止頻率的兩倍。使用1MHz的本地振蕩器頻率,針對圖中顯示的單個RC濾波器,計算出的帶通如圖5所示。
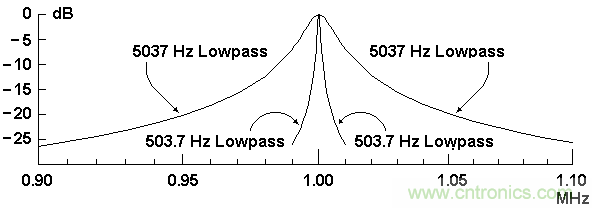
圖5:零頻率IF帶通。
要注意10:1的帶寬比與10:1的低通濾波器截止頻率比,它們為:1/(2 pi x 3160 x 0.01E-6) = 5037 Hz ...和... 1/(2 pi x 3160 x 0.1E-6) = 503.7Hz。
這項技術被應用于美國海軍CVA VAST測試系統的Building Block 38(BB38)中,BB38被稱為低頻波分析儀。但零頻IF并非 源于此,而是借鑒現已停產的惠普HP3590A分析儀。
然而,戲法只能玩一次。四混頻器可能會受到DC偏移的干擾。為避免這個問題,用極低頻高通角對低通濾波器實施直流阻斷。結果,IF帶通在中心頻率處具有無限深但非常窄的陷波。
本文轉載自電子技術設計。
推薦閱讀:







