【導讀】每個電路都有一定的噪聲,這些噪聲會影響模擬和數字電路的性能。有些噪聲來自外部干擾,有些噪聲則由熱效應等隨機因素引起。隨機產生的噪聲要比已知來源的噪聲更難以表征,因為沒有哪次測量提供了關于上一次或下一次測量的任何信息。這種過程只能通過對許多事件的多次測量、并用下次某個具體事件的概率來描述。許多數字示波器提供的工具可以用來表征噪聲。一旦了解了噪聲的特征,就有辦法減輕噪聲。
前言: 每個電路都有一定的噪聲,這些噪聲會影響模擬和數字電路的性能。有些噪聲來自外部干擾,有些噪聲則由熱效應等隨機因素引起。隨機產生的噪聲要比已知來源的噪聲更難以表征,因為沒有哪次測量提供了關于上一次或下一次測量的任何信息。這種過程只能通過對許多事件的多次測量、并用下次某個具體事件的概率來描述。許多數字示波器提供的工具可以用來表征噪聲。一旦了解了噪聲的特征,就有辦法減輕噪聲。
要用數字示波器分析諸如電氣噪聲等隨機信號,就需要能夠提供隨機過程多個視圖的工具。圖1是多維示波器工具的預覽圖。
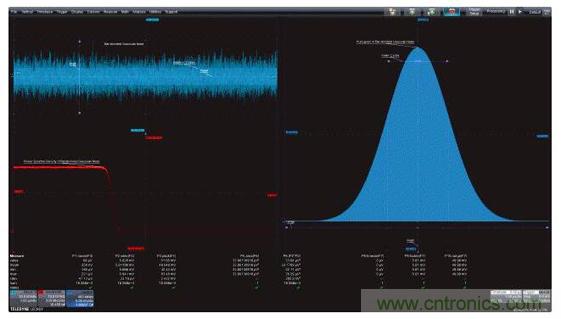
圖1:左上圖是帶寬受限的高斯噪聲的時域圖,左下圖是功率譜密度,是帶寬受限噪聲的頻域圖;右面的柱狀圖是帶寬受限噪聲的統計圖。這三個視圖都因采用了有助于對測量進行量化的測量參數而得到增強。
顯示在圖1左上部分的曲線是帶寬受限的高斯噪聲的時域圖。我們在整篇文章中引用的都是這個信號。下面的曲線顯示的是頻域中的噪聲:信號的功率譜密度(PSD)顯示了每赫茲的噪聲功率與頻率的關系。右圖是帶寬受限噪聲的柱狀圖,通過近似隨機過程的概率密度函數(PDF)提供統計視圖。這些曲線的下方顯示了一系列的測量參數,用于量化通過數學計算得到的波形。下面我們將詳細了解每種測量技術,看看每種方法能夠呈現帶寬受限噪聲信號哪些內容。
1、噪聲或抖動
噪聲和抖動是相互關聯的。噪聲是疊加到有用信號上的不想要的垂直信號分量;抖動是信號時序發生了不想要的變化。噪聲信號被施加到諸如邏輯門這樣的閾值比較器上時就變成了抖動。由垂直噪聲引起的幅度變化會使輸出早于或晚于閾值交越的理想時序。用于測量噪聲的工具和過程同樣可用于測量抖動。
對于接到示波器輸入通道的信號可以直接進行噪聲測量,抖動測量則是基于時序測量,比如時間間隔誤差(TIE)、周期或占空比。對輸入信號開展的這些時序測量都是一個周期一個周期進行的。使用稱為軌跡或時間軌跡的數學函數,可以將測量結果按時間繪制出來。這種軌跡函數就是隨后用于抖動測量的輸入信號。
2、時域
測量參數可以應用于圖2中的噪聲波形,以深入了解這種噪聲信號的特性。圖中顯示的參數有平均值、標準偏差和峰峰值。顯示器下方顯示了讀取的參數值。
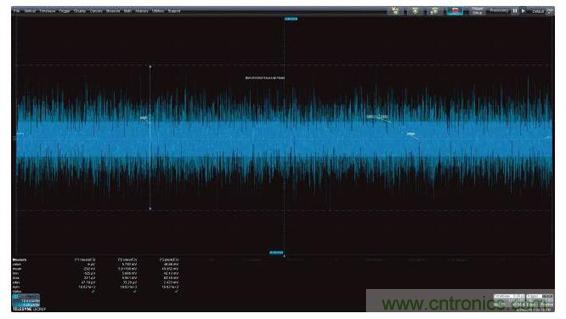
圖2:帶寬受限噪聲信號的時域圖。參數值顯示了基本測量、平均值、標準偏差或交流均方根、峰峰值。
參數標記在隨機波形上,圖形化顯示了測量結果。標準偏差也可以被稱為交流耦合的均方根(rms)值,因為它描述了波形的有效幅度,因此也許是最有用的。平均值是指信號的平均值,采集過程中出現的最大和最小幅度之差則用峰峰值表示。除了讀取指定采集過程的所選參數,示波器還可以計算和顯示多次采集后每種參數的累積統計結果,提供每種參數的均值、最大值、最小值和標準偏差。
2.1、柱狀圖:統計域視圖
隨機過程最好是在統計域中用柱狀圖進行描述。圖3顯示了上述帶寬受限的噪聲信號的柱狀圖及源波形。這張柱狀圖將滿刻度電壓范圍分為5000份,并計算落在每一范圍內的采樣值數量。垂直軸是每一范圍內的樣本數量,正比于該值發生的概率,水平軸是幅度值,本例中是電壓值。
帶寬受限噪聲信號的柱狀圖是經典的貝爾曲線,具有高斯或正常概率密度函數的特征。如果知道波形的方差(標準偏差的平方)和均值,就可以完整地描述概率密度函數。另外要注意,這種分布圍繞均值呈對稱特性。
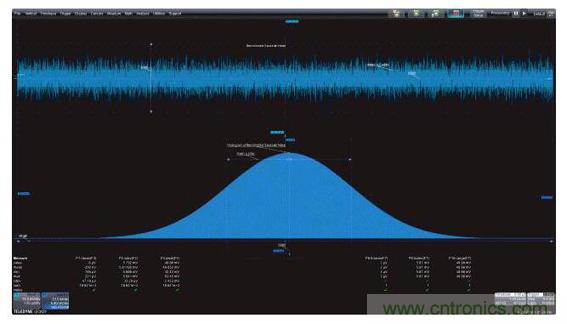
圖3:帶寬受限噪聲信號的柱狀圖呈現出典型的高斯貝爾形狀的響應。柱狀圖參數讀取柱狀圖均值、標準偏差和范圍。
測量參數也可以應用于柱狀圖。在這個例子中是柱狀圖均值(hmean)、標準偏差(hstdev)和范圍(hrange)。注意,這些讀數與前面測量時間波形得到的均值、標準偏差和峰峰值非常接近,兩者之間很小的差別是對柱狀圖樣本的“分割”造成的。
高斯分布圍繞均值呈對稱特性,隨著幅度遠離均值,幅度值的概率會下降。雖然極端幅度(稱為尾巴)發生的概率很低,但仍然是可能發生的。極端幅度不會到零意味著高斯分布是沒有邊界的。只要有足夠多的樣本,很大幅度的樣本也是有可能出現的。圖4顯示了一些典型的概率密度函數。高斯分布是最上面那個圖形。

圖4:包括高斯、瑞利、均勻和正弦在內的一組概率密度函數。
從上往下數第二張圖是瑞利分布。這是一種不對稱的分布,是將高斯分布噪聲施加到峰值檢測器造成的。這種分布表明概率密度函數不需要是對稱的。
從上至下數第三張圖是一種均勻分布。這種分布出現在時序測量中,比如觸發事件和示波器采樣第一個樣本之間的時間。在均勻分布中,所有樣值都具有相同的概率。這種分布是有邊界的。
最底下那張圖顯示的是同樣具有邊界約束的正弦分布。這種分布呈馬鞍形狀,最大概率發生在幅度極值點(最大和最小值點)。
在許多應用中,兩個或多個隨機過程可能發生交互。當這種情況發生時,過程的概率密度會進行數學卷積運算。一個常見的例子是結合了隨機和確定性抖動分量的時序抖動。圖5顯示了結合在一起的高斯和正弦分量,源分布位于上面兩張圖,從上往下數的第三張分布圖是兩個源卷積的結果。許多先進的示波器提供可選的抖動或噪聲分析包,這些分析包可以將這些組合式分布分開,單獨測量分量。
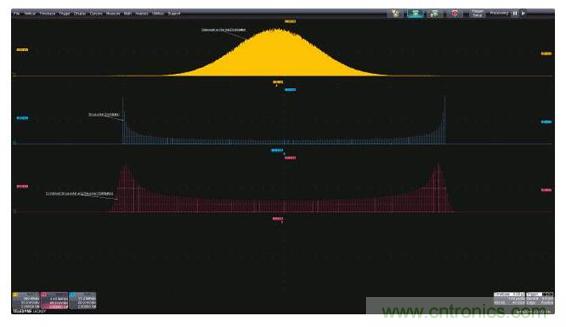
圖5:當高斯和正弦分布組合在一起時形成的概率密度函數是兩個源概率密度函數的卷積。
3、頻域分析
單位頻率上的功率(即功率譜密度PSD)是最常見的頻域噪聲分析工具。圖6給出了一個例子,上部是帶寬受限高斯噪聲的時域圖,下部是帶寬受限噪聲的功率譜密度。
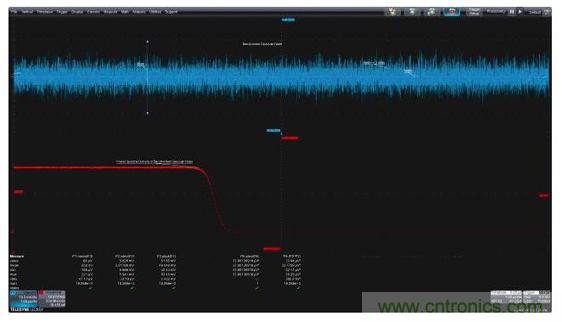
本例中功率譜密度的測量單位是V2/Hz。這條曲線是用示波器的快速傅里葉變換(FFT)計算出來的,選用的是輸出類型幅度平方而不是默認的分貝(dBm)刻度。除了輸出類型,我們還選擇了矩形加權和最小素因數FFT。這種FFT可以報告分辨率帶寬Δf,在本例中是100kHz,以及加權函數的有效噪聲帶寬(ENBW),針對矩形加權的值為1.000。
為了計算功率譜密度,平均后的FFT輸出必須被歸一化為有效FFT帶寬。此外,這個示波器的FFT輸出經校準可讀取峰值而不是均方根值。為了轉換回均方根值,FFT幅度值必須乘上0.707,幅度平方值必須乘上0.5。必須使用Rescale數學函數將FFT值除以FFT的有效帶寬才能將該值歸一化為單位帶寬(1Hz)。Rescale函數可以通過一個乘數因子并加減偏移量重新調整數值。在我們這個例子中,乘數是0.5/100E3 = 5E-6。乘數因子0.5在前面已經討論過。另外一個因子是有效FFT帶寬的倒數,是分辨率帶寬乘以等效噪聲帶寬(ENBW)。如果選擇了矩形以外的加權函數,ENBW將是大于1的值。Rescale函數還能改變單位,在本例中單位被設為V2/Hz。你可能已經注意到,再構造數學函數也已經用于將浮點FFT輸出的映射優化進參數測量中使用的整數數學空間。
參數P2測量時域波形的標準偏差參數。P6使用參數數學公式實現標準偏差的平方,得到噪聲信號的方差。參數P5代表功率譜密度曲線下方的面積,這個面積也是噪聲信號的方差,只不過是從功率譜密度計算出來的。兩種方法計算出來的方差值基本上是相等的,相差不到0.1%。
在頻域中分析隨機過程可以幫助你細分不同頻率產生的噪聲。本例中的面積測量可以覆蓋整個FFT范圍。你也可以使用測量選通門將測量限制在指定頻帶內,以判斷特定頻譜區域的噪聲情況。在帶寬等于FFT有效噪聲帶寬的情況下,示波器的光標可以讀取特定頻率處的功率譜密度。
4、派生參數
峰值因數,即波形峰值與均方根值之比,可以幫助你確定處理信號峰值變化所需的動態范圍。雖然我們使用的示波器沒有雙極性“峰值”參數,但我們借助通道1中信號的絕對值可以很容易地創建一個。這樣可以將負值“翻轉”進波形的正值區域,進而讓你使用最大值參數讀取每次采集數據的最大正峰或負峰值。注意,這種方法是因為信號有零均值才起作用的。然后我們就可以使用參數數學公式計算峰值與均方根值之比的峰值因數。圖7顯示了這種測量。
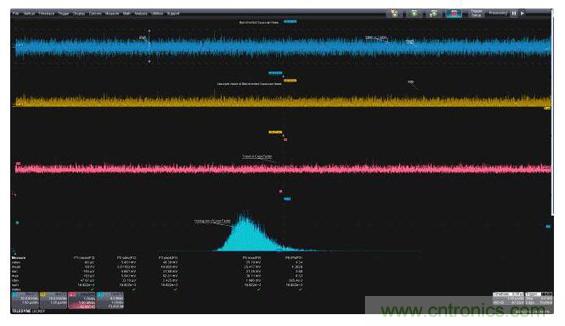
圖7:測量峰值與均方根值之比的信號峰值因數。所測信號的絕對值使得所有峰值呈單極性,因此最大值參數返回的就是每次采集數據的最大峰值。參數數學公式可計算出最大值與標準偏差(均方根)值之比值,即峰值因數。
最上邊的波形是帶寬受限的噪聲信號。參數P2是噪聲波形的標準偏差(交流耦合的均方根值)。下面一個波形顯示了噪聲波形的絕對值,這個波形是單極性的。源波形中的最高正負峰值已成為最高絕對峰值。使用最大值參數得到這個參數。
參數P5是絕對波形曲線的最大值。參數P6使用參數數學公式計算每次采集數據的峰值因數,即P5(max)與P2(rms)的比值。P6參數統計顯示了當前值、均值、最小最大標準偏差以及峰值因數測量值總數。在本例所示超過15000次采集中,峰值因數從3.68變到6.53,平均值為4.38。
從上往下第三張圖是峰值因數的趨勢曲線,按測量順序顯示了每一次測量的峰值因數。趨勢圖下方是峰值因數的柱狀圖。從圖中可以看出,峰值因數測量結果大多在均值附近,僅在均值的最右邊有少量的高值測量結果。
5、總結
你可以使用現代數字示波器中的時域、頻域和統計域工具量化諸如噪聲和抖動等隨機過程,并通過相關的測量參數進行增強。包括均值、標準偏差和范圍在內的統計參數可以幫助你了解被測的過程。參數數學公式可以推導出派生參數,比如方差和峰值因數。








