【導(dǎo)讀】即使是考慮到運(yùn)放所有的已知及未知阻抗負(fù)載,運(yùn)算放大器的輸出中始終含有無法基于輸入信號(hào)和完全已知的閉環(huán)傳遞函數(shù)進(jìn)行預(yù)測的信號(hào)。這種不確定信號(hào)被稱為噪聲。
導(dǎo)致噪聲產(chǎn)生的因素可能是放大器電路本身,可能是其反饋環(huán)路中使用的元件,也可能是電源;噪聲也可能從附近(或較遠(yuǎn)的地方)的噪聲源藕合或感應(yīng)至輸入、輸出、地回路或測量電路之中的。
無疑,我們對(duì)噪聲的關(guān)注程度取決于兩點(diǎn):
● 電路在目標(biāo)頻段所要達(dá)到的分辨率;
● 避免噪聲轉(zhuǎn)移至非直接相關(guān)頻段。
由于運(yùn)算放大器多用作前置放大器和高精度信號(hào)處理器,運(yùn)算放大器電路的精度日益受到關(guān)注。所以今天我們就談?wù)劇驹肼暸c運(yùn)算放大器電路】。
從噪聲角度來看,運(yùn)算放大器具有獨(dú)特的優(yōu)勢,完全適用于低壓和高精度電路,因?yàn)?
● 可以選擇特定的放大器傳遞函數(shù),使其僅允許目標(biāo)頻段通過。
● 可以從具有不同噪聲特性的眾多型號(hào)中選擇適應(yīng)具體需要的放大器,以便在目標(biāo)頻段內(nèi)獲得近乎理想的特性。
● 如果噪聲源已知且經(jīng)過正確評(píng)估,則可預(yù)測各種放大器電路的噪聲情況并達(dá)到足夠的精度,從而為初步的手工設(shè)計(jì)提供依據(jù),并具有一定的成功驗(yàn)證的可能性。
基本模型一一電壓噪聲與電流噪聲
可將差分運(yùn)算放大器視為理想的無噪聲放大器,其噪聲電流源位于各輸入引腳與共模地之間,噪聲電壓源實(shí)際與某一側(cè)輸入引腳串聯(lián)。該模型與失調(diào)分析2中用到的EOS一Ibias模型非常類似,這不足為奇,因?yàn)榭蓪OS和Ibias視為直流噪聲源,可按時(shí)間、溫度等參數(shù)進(jìn)行調(diào)制。
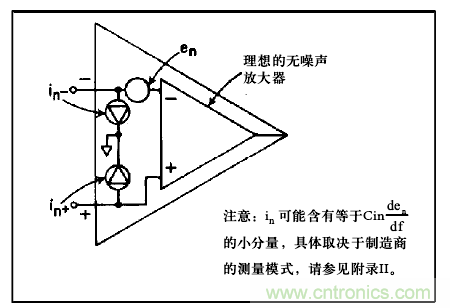
圖1.電壓與電流噪聲模型
在多數(shù)實(shí)際應(yīng)用中,可將噪聲電壓源和噪聲電流源視為彼此獨(dú)立的。如果暫時(shí)忽略電路和放大器的動(dòng)態(tài)范圍因素,就如EOS和Ibias一樣,噪聲的瞬時(shí)電壓分量可通過低阻抗、高增益電路進(jìn)行測量(圖2),而瞬時(shí)電流分量則可在一個(gè)很大(理想地“無噪聲的”)電阻中進(jìn)行測量。如果en與in之間無交互作用,則噪聲電壓測量輸出將與(1 + R2/R1)成比例,而噪聲電流測量輸出則僅與R2成比例。
請注意,這兩類噪聲的瞬時(shí)和(出現(xiàn)于放大器輸出端)為
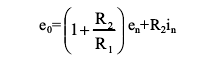
且在以下等式成立時(shí),en和in的相對(duì)噪聲貢獻(xiàn)相等
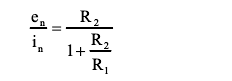
即條件為 : R2和R1的并聯(lián)等于en與in之比。當(dāng)阻抗水平高于en/in時(shí),電流噪聲占據(jù)主導(dǎo)。en和in均方根值之比有時(shí)被稱為放大器在既定帶寬下的“特征噪聲電阻”,在選擇與既定阻抗相匹配的放大器時(shí)可當(dāng)作實(shí)用的品質(zhì)因素,反之亦然。
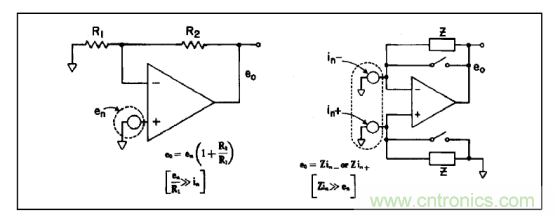
圖2. en和in的基本測量法(窄帶和點(diǎn)噪聲測量中需使用濾波器)
在已知電壓和阻抗的情況下,可將從外部源藕合至放大器輸入引腳的噪聲視為附加性的電壓信號(hào),或當(dāng)這種信號(hào)的產(chǎn)生取決于放大器的某種測量方式時(shí),也可視為附加性電流信號(hào),簡示為圖3。
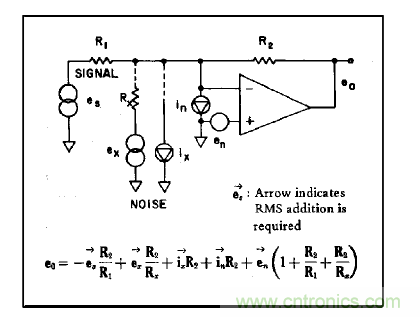
圖3.內(nèi)部和外部噪聲源的貢獻(xiàn)
噪聲增益與信號(hào)增益
圖4所示為一種反相放大器的基本反饋模型,其中含有數(shù)個(gè)阻性輸入引腳。對(duì)于較大的環(huán)路增益值(Aβ),電壓噪聲的噪聲增益實(shí)際為1/β。
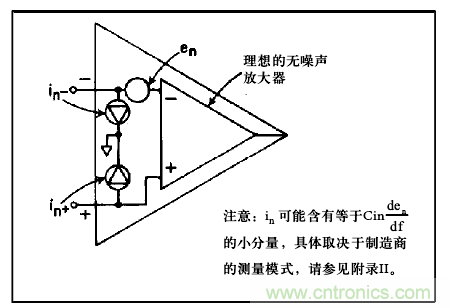
圖1.電壓與電流噪聲模型
如果Aβ不是遠(yuǎn)高于單位增益,則可使用以下更精確的表達(dá)式
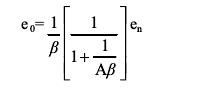
相對(duì)應(yīng)的電流噪聲表達(dá)式為
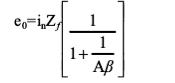
需要注意的是,對(duì)于無源反饋元件,1/β不會(huì)小于單位增益值,而且對(duì)于任意輸入信號(hào),該值也大于閉環(huán)增益。因此,即使信號(hào)增益小于單位增益,或者信號(hào)帶寬較窄,但en的總頻譜將出現(xiàn)在輸出端,其值至少等于單位增益。
同時(shí)需要注意,一般情況下,當(dāng)A和β均為動(dòng)態(tài)表達(dá)式時(shí),如果環(huán)路增益的相移一定程度上高于900,則放大器在接近Aβ=1時(shí)的頻率范圍處于欠阻尼狀態(tài),則該頻率下的噪聲增益的峰值可能高于單位增益很多,盡管信號(hào)增益在較低的頻率時(shí)就會(huì)平滑滾降。圖5為一種簡單明了、易于理解的示例。
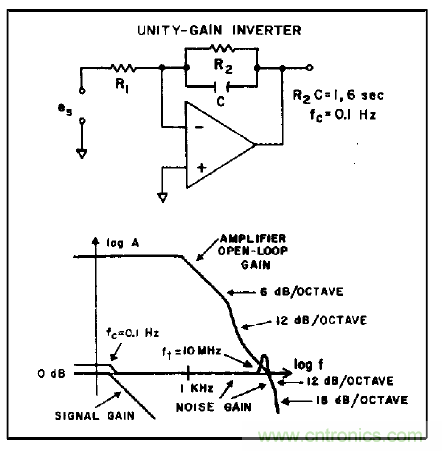
圖 5.噪聲帶寬與信號(hào)帶寬
如何表征噪聲
周期性重復(fù)噪聲可基于重現(xiàn)率、波形和幅度進(jìn)行描寫(如斬波器噪聲)。不規(guī)則噪聲則只能通過其波形和幅度進(jìn)行描寫,因?yàn)槠渥兓療o規(guī)律可言(在某種程度上來說,爆米花噪聲屬于此類)。無重復(fù)性波形的非周期性噪聲一般通過其統(tǒng)計(jì)特性進(jìn)行描述:均方根值、峰值和頻率成分。
均方根值。多數(shù)隨機(jī)噪聲都存在以下特性:如果求平均值間隔較長,結(jié)果得到的均方根值具有較大的可重復(fù)性。因此,以均值法基于較長間隔求得的目標(biāo)帶寬均方根值,是確定這類隨機(jī)噪聲特性行之有效的方式。目前為止,這是廠商和客戶都比較接受的估計(jì)噪聲各因素的最簡便方式。電壓均方根值定義如下
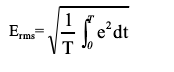
其中
Erms=均方根電壓值
T=觀測時(shí)間間隔
e=瞬時(shí)噪聲電壓
其中參數(shù)替換為瞬時(shí)電流值 i,則得到 Irms,即均方根電流值。進(jìn)行均方根測量時(shí),必須使用“真均方根”計(jì)量儀,也可將交流平均值(正弦波均方根校準(zhǔn)型計(jì)量儀)的讀數(shù)乘以因數(shù)1.13。
峰值。噪聲也可表征為任意間隔觀察到的最大正幅度與最大負(fù)幅度之差。在某些應(yīng)用中,當(dāng)峰峰值噪聲可能限制系統(tǒng)性能時(shí),可能需要采用峰峰測量法。
然而,從實(shí)用角度來看,由于噪聲幅度分布呈高斯分布,因此最高噪聲幅度的概率最低(但不為零),難以重復(fù)測得峰峰值噪聲。由于均方根值容易重復(fù)測得,而且是噪聲數(shù)據(jù)公認(rèn)的、最常用的表示方式,因此可利用下表估算在給定均方根的情況下,超過各種峰值的概率。
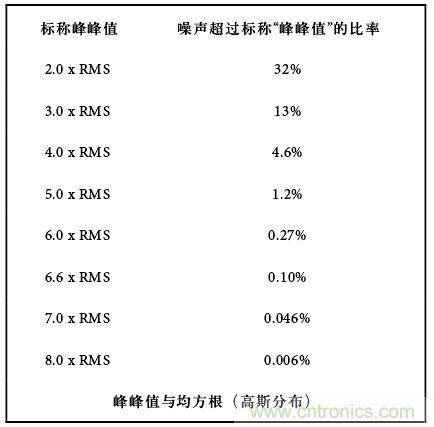
一般觀測到的峰峰噪聲值在3 x RMS與8 x RMS之間,取決于觀測者的耐心及可用數(shù)據(jù)量。在較高的強(qiáng)度下才能觀測到示波器的蹤跡,然而由于大量平均求值運(yùn)算是在低強(qiáng)度完成,此時(shí)將產(chǎn)生一個(gè)較為接近均方根值的結(jié)果。另外,市場上用于自動(dòng)測量這類參數(shù)的峰值幅度分布分析儀也日益增多。
干擾噪聲與固有噪聲
既定電路的噪聲可分為兩個(gè)基本類別,即干擾噪聲(指自電路外部拾取的噪聲)和固有噪聲(指電路內(nèi)部產(chǎn)生的噪聲)。
干擾噪聲可能具有周期性,可能不規(guī)則重復(fù),也可能完全隨機(jī),通過以下預(yù)防措施,往往可以大幅減少(或防止)這類噪聲。比如,采取預(yù)防措施針對(duì)由電源線頻率和諧波、無線電廣播站、機(jī)械開關(guān)電弧以及阻性電路中開關(guān)帶來的電流或電壓尖峰等所引起的電磁干擾進(jìn)行改善。這類預(yù)防措施包括濾波、去藕、對(duì)引線和元件進(jìn)行靜電和電磁屏蔽、使用防護(hù)電位、消除地環(huán)路、對(duì)引線和元件位置方向重新排布、在繼電線圈中使用阻尼二極管、盡可能選用低電路阻抗、低噪型電源和基準(zhǔn)源等。振動(dòng)引發(fā)的干擾噪聲可通過機(jī)械設(shè)計(jì)改善。圖6中的表格列出了部分干擾噪聲源、其典型值及處理方式。

圖6.典型的干擾噪聲源
然而,即使所有干擾噪聲均得到消除,仍然存在固有噪聲。固有噪聲通常本質(zhì)上屬于隨機(jī)噪聲,多出現(xiàn)在電阻和半導(dǎo)體元件中,如晶體管和二極管等。(非隨機(jī)固有噪聲的一個(gè)例子是斬波器穩(wěn)壓型放大器中的斬波器噪聲。)電阻元件中產(chǎn)生的隨機(jī)噪聲被稱為約翰遜噪聲(也稱熱噪聲)。半導(dǎo)體元件中產(chǎn)生的隨機(jī)噪聲可能屬于以下三類之一:肖特基噪聲(或稱散粒噪聲)、閃爍噪聲(1/f噪聲)和爆米花噪聲。
推薦閱讀:







