【導讀】作為一個工程師,很多人對隨機振動看著熟悉,卻又實際陌生。熟悉是因為幾乎每個產品在出廠時都要求要做隨機振動試驗,陌生是因為當面對用戶所給的功率密度譜有時會感到很茫然,尤其是這個功率譜的單位居然是 ,簡直是反人類,為啥整這么麻煩,不能給個加速度 直接振嗎?哈哈,這個還真不能,下面咱們就來抽絲剝繭,看看隨機振動功率密度譜到底是咋個回事?
一、隨機信號和正太分布有什么關系?
作為一個工程師,很多人對隨機振動看著熟悉,卻又實際陌生。熟悉是因為幾乎每個產品在出廠時都要求要做隨機振動試驗,陌生是因為當面對用戶所給的功率密度譜有時會感到很茫然,尤其是這個功率譜的單位居然是 ,簡直是反人類,為啥整這么麻煩,不能給個加速度 直接振嗎?哈哈,這個還真不能,下面咱們就來抽絲剝繭,看看隨機振動功率密度譜到底是咋個回事?
隨機振動,是因為振動源是隨機信號,顧明思議,就是信號的發生帶有隨機性,無法用一個明確的函數把它表達出來,一個典型的隨機信號大概長這個樣子:
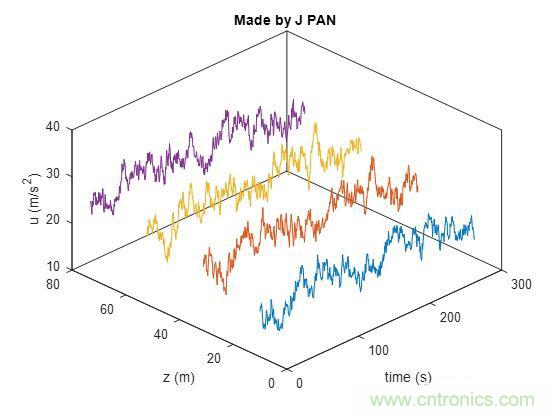
可以看出,乍一看完全沒有規律可言,高度不規則,無規律的,不可預估也不可重復,每次測量都不一樣。那隨機信號是不是就是不可描述的呢?首先我們研究一下什么是隨機,隨機對應不確定性,不確定性在物理學和數學上是一個不受歡迎的詞,老板問你圖紙什么時候畫完,你敢回答“隨機吧”,或者更佛系一點“隨緣吧”?相信等待你的可不僅僅是白眼哦,這也是為啥當初波恩將概率解釋引入到量子力學時受到愛因斯坦強烈的反對,“上帝是不擲骰子”的典故便來源于此。然后諸多證據表明:也許隨機是這個世界的本質特性之一,這可以由一個著名的數學定理來證明:中心極限定理。
一、隨機信號和正太分布有什么關系
中心極限定理有一組,但基本可以用一句通俗的話來概括它們:大量相互獨立的隨機變量,其平均值正態分布。對中心極限定理最形象的解釋是高爾頓釘板實驗:小球在下落過程中碰到很多個釘子,每次碰撞都是一個二項式的隨機過程:以同等的概率通過釘子左側或者右側,小球最后到達的位置,是這很多個“左右”隨機變量相加后的平均位置。不難看出,這個平均值落在中心處的概率最大,小球聚集最多,但也可能向左或向右偏,偏離越大,小球的數目越少,不同位置的不同小球數便形成了一個“分布”,中心極限定理則是從數學上證明了,這個分布的極限是正態分布。
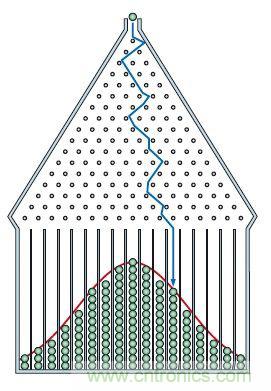
高爾頓釘板實驗實質上是一組二項式分布,從數學上還可以證明:中心極限定理的條件可以從二項分布推廣到獨立同分布隨機序列,以及不同分布的隨機序列。也就是說:在一定條件下,各種隨意形狀概率分布生成的隨機變量,它們加在一起的總效應,是符合正態分布的。
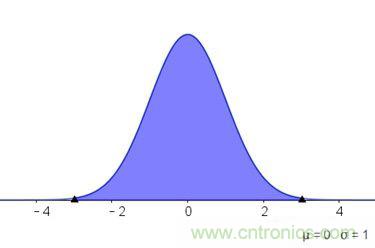
這也是為啥正太分布這么常見的原因,因為實際上的隨機生物過程或物理過程,都不是只由一個單獨的原因產生的,它們受到各種各樣隨機因素的影響。比如產品加工免不了有誤差,而誤差形成的原因五花八門,各種各樣。就算我們打開上帝視角,夠分別清楚產生誤差的每種單一原因,誤差的分布曲線可能不是高斯的,但是,所有誤差加累計在一起時,通常得到一個正態分布。下圖是30組隨機變量,和值隨數據增加時分布情況。
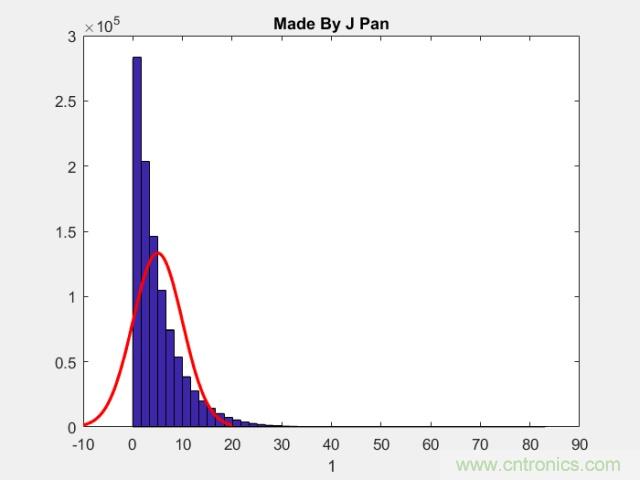
30組隨機變量(每組100萬數據),和值的隨數據增加時分布情況
總之,中心極限定理告訴我們:無論引起過程的各種因素的基本分布是什么樣的,當實驗次數 充分大時,所有這些隨機分量之和近似是一個正態分布的隨機變量。也就是說:對于平穩隨機過程而言,其分布是趨于正太的。
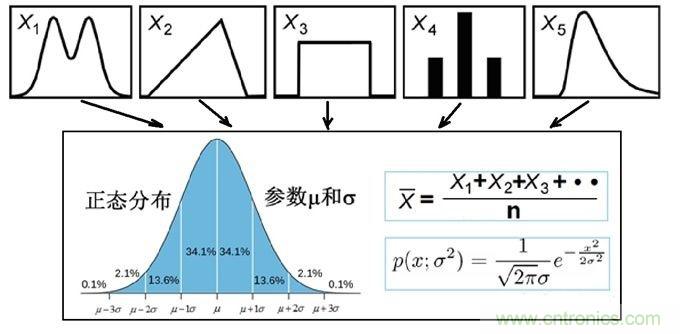
我們知道,正太分布的概率密度的表達式為:
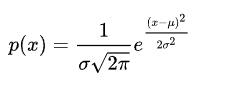
其中![[公式]](https://www.zhihu.com/equation?tex=%5Cmu) 為數學期望,代表著信號的平均值,
為數學期望,代表著信號的平均值,
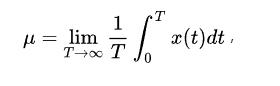 ,
,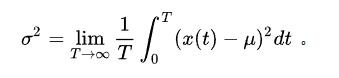 。
。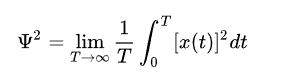
很容易得到:
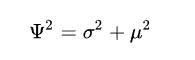
所以當平均值為零的時候,均方值與方差相等。從圖形上看,平均值![[公式]](https://www.zhihu.com/equation?tex=%5Cmu) 決定了正太分布的位置,均方根值,也就是標準差
決定了正太分布的位置,均方根值,也就是標準差 ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma) ,決定了分布的幅度。如果正態分布概率密度一旦確定,其數學期望
,決定了分布的幅度。如果正態分布概率密度一旦確定,其數學期望![[公式]](https://www.zhihu.com/equation?tex=%5Cmu) 和方差
和方差![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2) 也就確定了。對于隨機信號而言,數學期望
也就確定了。對于隨機信號而言,數學期望![[公式]](https://www.zhihu.com/equation?tex=%5Cmu) 基本為零(或者去除直流分量后為零),所以唯一確定的量就剩均方值,此時均方值和方差一致,并且
基本為零(或者去除直流分量后為零),所以唯一確定的量就剩均方值,此時均方值和方差一致,并且
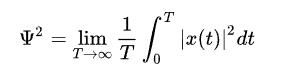
如果仔細觀察上式,可以發現,從量綱來看, ![[公式]](https://www.zhihu.com/equation?tex=%5Cint_%7B0%7D%5E%7BT%7D%5Cleft%7C+x%28t%29+%5Cright%7C%5E2dt) 代表了能量概念,而方差
代表了能量概念,而方差![[公式]](https://www.zhihu.com/equation?tex=%7B%5Cfrac%7B1%7D%7BT%7D%7D%5Cint_%7B0%7D%5E%7BT%7D%5Cleft%7C+x%28t%29+%5Cright%7C%5E2dt) 代表了平均功率概念。
代表了平均功率概念。
前面我們說到,平穩隨機信號是趨于正太分布的,決定正太分布的兩個參數:平均值 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu) 基本為零(不為零時,直流分量也很容易處理),唯一能表征隨機信號的就剩均方值(
基本為零(不為零時,直流分量也很容易處理),唯一能表征隨機信號的就剩均方值(![[公式]](https://www.zhihu.com/equation?tex=%5Cmu%3D0) 時等于方差)
時等于方差)![[公式]](https://www.zhihu.com/equation?tex=%5CPsi%5E2) ,也就是平均功率了。再具體一點,對于平穩隨機信號而言,描述
,也就是平均功率了。再具體一點,對于平穩隨機信號而言,描述![[公式]](https://www.zhihu.com/equation?tex=x%28t%29) 是沒有意義的,描述平均功率才有意義。如何才能描述平均功率呢?這時我們就要用到頻譜分析的概念了,可能有些人會覺得這個概念很生疏,我要說我們每天一睜眼就在進行譜分析你會信嗎?事實還真是這樣。我們的眼睛就是一雙最精密的譜分析儀:過濾到可見光以外的所有光線,并且可見光按照頻譜(頻率)進行精確分類。
是沒有意義的,描述平均功率才有意義。如何才能描述平均功率呢?這時我們就要用到頻譜分析的概念了,可能有些人會覺得這個概念很生疏,我要說我們每天一睜眼就在進行譜分析你會信嗎?事實還真是這樣。我們的眼睛就是一雙最精密的譜分析儀:過濾到可見光以外的所有光線,并且可見光按照頻譜(頻率)進行精確分類。
我們知道光本質是一種電磁波,既然是波,就有波長 ![[公式]](https://www.zhihu.com/equation?tex=%5Clambda) 和波動頻率
和波動頻率 ![[公式]](https://www.zhihu.com/equation?tex=f) ,光速
,光速 ![[公式]](https://www.zhihu.com/equation?tex=c%3D%5Clambda%5Ccdot+f) 一個定值,波長和波動頻率成反比。人眼可識別出波長在400納米至700納米的光線,并且根據波長不同(頻率不同)將可見光分成紅、橙、黃、綠、藍、靛、紫色。
一個定值,波長和波動頻率成反比。人眼可識別出波長在400納米至700納米的光線,并且根據波長不同(頻率不同)將可見光分成紅、橙、黃、綠、藍、靛、紫色。
當我們說“一個東西的表面是紅色”的時候,這是正常人的定性描述,換成喜歡定量描述(裝X)工程師會怎么說呢?“這個東西表面特性會選擇性反射一種電磁波,這種電磁波波長約700納米,波動頻率 約![[公式]](https://www.zhihu.com/equation?tex=5%5Ctimes10%5E%7B14%7D) 赫茲”。
赫茲”。
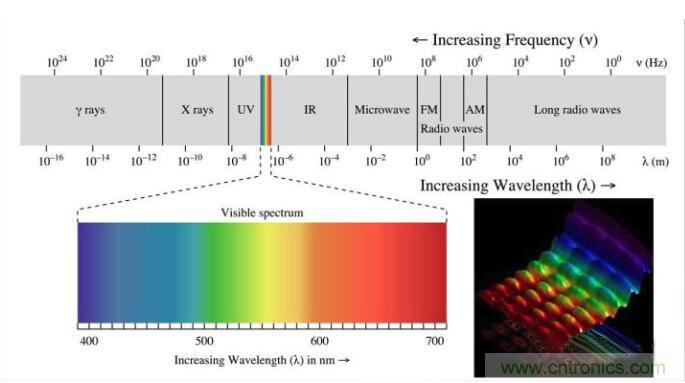
那頻譜分析是什么呢?它是一種將復雜號分解為較簡單信號的技術,許多物理信號均可以表示為許多不同頻率簡單信號的和,找出一個信號在不同頻率下的信息(可能是幅度、功率、強度或相位等)的作法就是頻譜分析。比如通過一個三棱鏡就可進行色散試驗,將白光分解成頻率各不相同的單色光,我們經常在雨后見到的彩虹也是一種色散現象。
在傅里葉變換背后到底有什么小秘密 這篇文章中,我們介紹了傅里葉變換概念,它是頻譜分析的基礎,這篇文章中介紹了復指數函數是如何構成一個完備正交基的,以及如何進行傅里葉變換及其逆變換。但是,說這么多,頻譜分析和隨機信號有什么關系?
二、時域、頻域之間功率守恒?
頻譜分析和平穩隨機信號可以通過一個叫“帕斯瓦定理”的公式聯系起來,一個經常被低估的定理,大概長這個樣子:
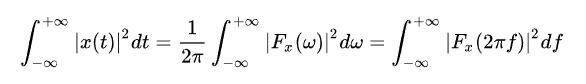
其中 ![[公式]](https://www.zhihu.com/equation?tex=F%28%5Comega%29) 是
是 ![[公式]](https://www.zhihu.com/equation?tex=x%28t%29) 的傅里葉變換,這個公式看著還挺對稱,被積函數都是自變量的平方,貌似蘊含著什么深刻的意義。翻譯過來,這個定理說的是什么事呢?那就是信號的能量(或者平均功率)無論在時域看,還是在頻域看,都是一樣的。
的傅里葉變換,這個公式看著還挺對稱,被積函數都是自變量的平方,貌似蘊含著什么深刻的意義。翻譯過來,這個定理說的是什么事呢?那就是信號的能量(或者平均功率)無論在時域看,還是在頻域看,都是一樣的。
人類習慣于在時域觀察一個信號,那會不會存在另一個物種或者空間,他們喜歡在頻域觀察呢?但無論如何,帕斯瓦定理告訴我們,不論頻域還是時域,信號所代表的能量是守恒的,而守恒的本質是對稱性,那是不是預示著時域和頻域有著某種高度的對稱呢?
好了,扯遠了,哲學上的事情不歸工程師管,我們要所的事情就是如何定量化的的去描述不確定的東西,比如隨機信號。前面我們說了,平穩隨機信號 ![[公式]](https://www.zhihu.com/equation?tex=x%28t%29) 的幅值是呈現正太分布的,其平均值接近為零(或去除直流分量后),均方值或方差(也就是平均功率)是固定的,既然平均功率(或能量)在時域和頻域是守恒的,而在時域
的幅值是呈現正太分布的,其平均值接近為零(或去除直流分量后),均方值或方差(也就是平均功率)是固定的,既然平均功率(或能量)在時域和頻域是守恒的,而在時域 ![[公式]](https://www.zhihu.com/equation?tex=x%28t%29) 是隨機的,不可描述,那我們可以換到頻域去啊:
是隨機的,不可描述,那我們可以換到頻域去啊:
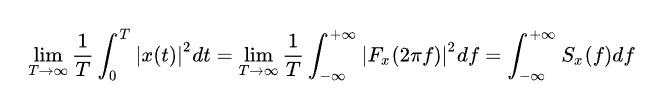
其中: ![[公式]](https://www.zhihu.com/equation?tex=S_x%28f%29%3D%5Clim_%7BT+%5Crightarrow+%5Cinfty%7D%5Cfrac%7B1%7D%7BT%7D%7B%5Cleft%7C+F_x%282%5Cpi+f%29+%5Cright%7C%5E2%7D) ,
, ![[公式]](https://www.zhihu.com/equation?tex=S_x%28f%29) 表示了信號的平均功率(或能量)在頻域上的分布,即單位頻帶的功率隨頻率變化的情況,故稱之為信號的自功率譜密度函數,簡稱自功率譜或自譜。
表示了信號的平均功率(或能量)在頻域上的分布,即單位頻帶的功率隨頻率變化的情況,故稱之為信號的自功率譜密度函數,簡稱自功率譜或自譜。 ![[公式]](https://www.zhihu.com/equation?tex=S_x%28f%29) 與
與 ![[公式]](https://www.zhihu.com/equation?tex=f) 軸包圍的面積等于信號
軸包圍的面積等于信號![[公式]](https://www.zhihu.com/equation?tex=x%28t%29) 的平均功率,即
的平均功率,即![[公式]](https://www.zhihu.com/equation?tex=x%28t%29) 的幅值分布的方差或均方值。同時可以看出,當
的幅值分布的方差或均方值。同時可以看出,當 ![[公式]](https://www.zhihu.com/equation?tex=x%28t%29) 表示加速度時(單位為
表示加速度時(單位為 ![[公式]](https://www.zhihu.com/equation?tex=g) ),
),![[公式]](https://www.zhihu.com/equation?tex=S_x%28f%29) 的單位就變成了
的單位就變成了![[公式]](https://www.zhihu.com/equation?tex=g%5E2%2FHz) 。
。
三、自相關又是個什么玩意?
現在,事情就貌似變得簡單了,我們將時域信號![[公式]](https://www.zhihu.com/equation?tex=x%28t%29) 進行傅里葉變換,得到頻域分布
進行傅里葉變換,得到頻域分布 ![[公式]](https://www.zhihu.com/equation?tex=F%28%5Comega%29) ,然后平方積分就可以得到功率譜密度了啊。理論上,我們確實可以這么做,但是實際上,這樣做有一個小困難,那就是經典傅里葉變換不是一直存在的,前提的:信號
,然后平方積分就可以得到功率譜密度了啊。理論上,我們確實可以這么做,但是實際上,這樣做有一個小困難,那就是經典傅里葉變換不是一直存在的,前提的:信號 ![[公式]](https://www.zhihu.com/equation?tex=x%28t%29) 絕對值可積,即
絕對值可積,即 ![[公式]](https://www.zhihu.com/equation?tex=%5Cint_%7B-%5Cinfty%7D%5E%7B%2B%5Cinfty%7D%5Cleft%7C+x%28t%29+%5Cright%7Cdt%5Cprec+%2B%5Cinfty) ,而實際上平穩隨機變量是不滿足的。
,而實際上平穩隨機變量是不滿足的。
為了解決隨機信號的傅里葉變換問題,我還得引入一個概念:自相關,先看定義:隨機過程 ![[公式]](https://www.zhihu.com/equation?tex=x%28t%29) 的自相關函數定義為在時刻
的自相關函數定義為在時刻![[公式]](https://www.zhihu.com/equation?tex=t) 和時刻
和時刻![[公式]](https://www.zhihu.com/equation?tex=t%2B%5Ctau) 的隨機變量乘積的平均值,
的隨機變量乘積的平均值,![[公式]](https://www.zhihu.com/equation?tex=%5Ctau) 是時移,當平均時間
是時移,當平均時間 ![[公式]](https://www.zhihu.com/equation?tex=T%5Crightarrow%5Cinfty) 時,平均值的極限便是自相關函數,其數學表達式為:時,平均值的極限便是自相關函數,其數學表達式為:
時,平均值的極限便是自相關函數,其數學表達式為:時,平均值的極限便是自相關函數,其數學表達式為:
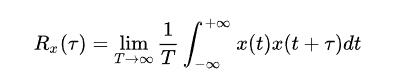
定義有點拗口,可以先不理解,它說明一個什么事呢?它反映了隨機信號本身在不同時刻的相互關系,再直白一點:把一個信號平移一段距離,跟原來有多相似。我們都知道,重要的證件上的照片,一般都要求是近半年的,道理顯而易見,時間久了跟現在長得可能就不一樣了。下圖顯示了C羅近十年容顏的變化,都說女大十八變(即使不整容),男的又何嘗不是。

很顯然的一點是:隨著時間的推移,C羅的長相是發生明顯變化的,時間越短,長相越接近,可以想象,當時間足夠長后,不知道我們還能不能認出他來,不信,你看:

馬爸爸不要告我
對于隨機信號,特別白噪聲隨機信號來說,當時移![[公式]](https://www.zhihu.com/equation?tex=%5Ctau) 非常小時,
非常小時, ![[公式]](https://www.zhihu.com/equation?tex=x%28t%29) 和
和 ![[公式]](https://www.zhihu.com/equation?tex=x%28t%2B%5Ctau%29) 相差很小的概率很大,這時
相差很小的概率很大,這時![[公式]](https://www.zhihu.com/equation?tex=R_x%28%5Ctau%5Crightarrow0%29) 值非常大,表示關系密切。特別當
值非常大,表示關系密切。特別當 ![[公式]](https://www.zhihu.com/equation?tex=%5Ctau%3D0) 時,
時, ![[公式]](https://www.zhihu.com/equation?tex=R_x%28%5Ctau%3D0%29) 值最大,等于方均值,也就是平均功率,表示完全相關。
值最大,等于方均值,也就是平均功率,表示完全相關。
當時移 ![[公式]](https://www.zhihu.com/equation?tex=%5Ctau) 較大時,
較大時, ![[公式]](https://www.zhihu.com/equation?tex=x%28t%29) 和
和 ![[公式]](https://www.zhihu.com/equation?tex=x%28t%2B%5Ctau%29) 相差很小的概率很小。作平均計算正負對消,
相差很小的概率很小。作平均計算正負對消,![[公式]](https://www.zhihu.com/equation?tex=R_x%28%5Ctau%29) 值很小。并且隨著
值很小。并且隨著![[公式]](https://www.zhihu.com/equation?tex=%5Ctau) 值的增大,
值的增大,![[公式]](https://www.zhihu.com/equation?tex=R_x%28%5Ctau%5Crightarrow%5Cinfty%29) 值很快衰減到零,表示
值很快衰減到零,表示![[公式]](https://www.zhihu.com/equation?tex=x%28t%29) 和
和![[公式]](https://www.zhihu.com/equation?tex=x%28t%2B%5Ctau%29) 之間沒有依賴關系,對一般的寬帶隨機振動,時間間隔很遠的二個隨機量之間不存在任何固定關系。簡單點來說:對于平穩隨機信號,自相關函數將信號的平均功率向
之間沒有依賴關系,對一般的寬帶隨機振動,時間間隔很遠的二個隨機量之間不存在任何固定關系。簡單點來說:對于平穩隨機信號,自相關函數將信號的平均功率向 ![[公式]](https://www.zhihu.com/equation?tex=%5Ctau%3D0) 這一點集中,
這一點集中,![[公式]](https://www.zhihu.com/equation?tex=%5Ctau%5Cne0) 時自相關函數快速衰減為零。
時自相關函數快速衰減為零。
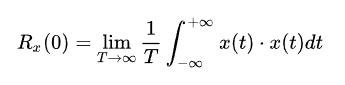
對于周期信號,自相關函數可以把隨機信號中的周期成份檢測出來,這是因為任何周期信號在所有的時移上都有一定形狀的自相關函數圖形。對于周期信號來說,經過一個周期后又精確的重復過去的時間歷程,因此當時移超過該周期時,其自相關函數必然重復前一段的形狀。
所以若在自相關函數圖上發現時移趨于無窮大, ![[公式]](https://www.zhihu.com/equation?tex=R_x%28%5Ctau%5Crightarrow%5Cinfty%29%5Cne0) ,而有某種周期性,則說明該隨機振動信號混有周期信號成分。 簡單點來說:自相關函數能夠檢測出信號內部蘊藏的周期組分,而過濾掉了周期組分的相位信息。
,而有某種周期性,則說明該隨機振動信號混有周期信號成分。 簡單點來說:自相關函數能夠檢測出信號內部蘊藏的周期組分,而過濾掉了周期組分的相位信息。
對于上面兩段話不是很理解的,可以看下面兩幅圖,分別是白噪聲隨機信號和隨機相位正弦信號及其自相關信號。
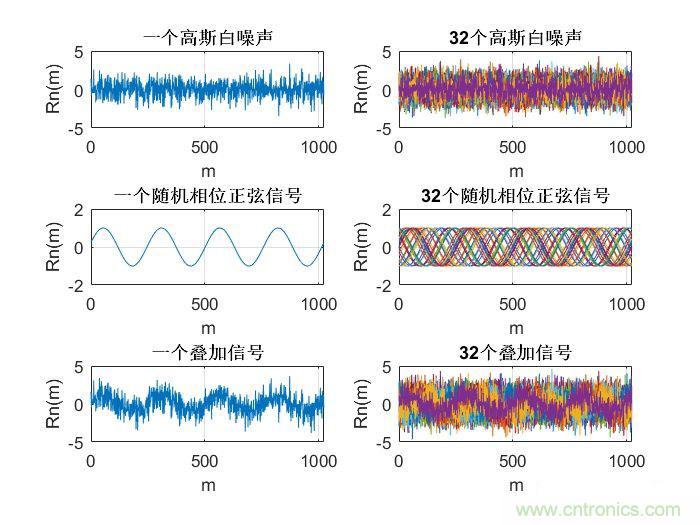
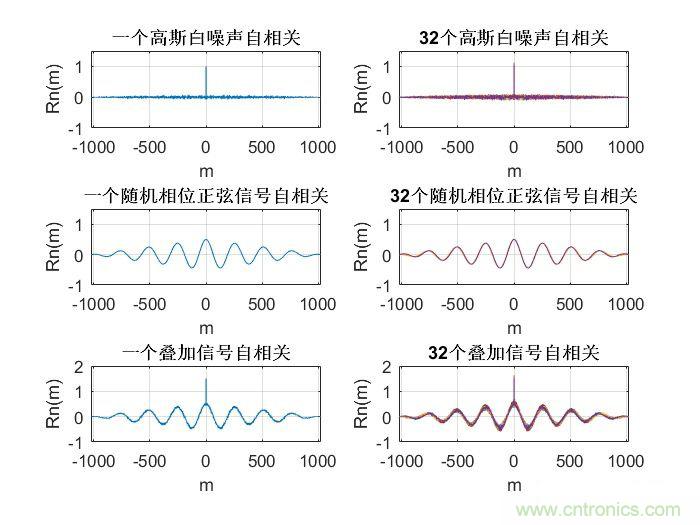
說了這么多,和我們要進行功率譜分析有什么關系?前面我們分析了,信號的功率在時域和頻域都是滿足守恒定律的,
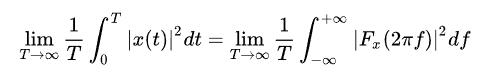
而功率被定義成幅值的平方的時間平均分量,而這個過程,也可以看成是去除頻域諧波分量的相位信息的過程,因為本質來說,一個簡諧信號的相位是不影響其功率的。而自相關函數,也具有去除信號相位的功能,那自相關函數和功率密度譜是不是有什么深刻的聯系呢?答案是肯定的,那就是維納-辛欽定理(Wiener–Khinchin theorem),這個定理表明:信號的自相關函數與功率密度譜是一對傅里葉變換對:
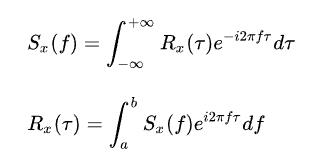
也就是說:一個信號的功率密度譜,就是其自相關函數的傅里葉變換。
總結一下整個邏輯:對于一個隨機信號而言,時域信息是雜亂無章的,唯一的確定性信息但是在統計意義下得到的,即幅值呈正太分布,均方值也就是平均功率是固定的。根據帕斯瓦定理,信號的平均功率在時域和頻域是守恒的,按道理說直接對時域信號進行傅里葉變換再取平方就可以。
但不幸的事,隨機信號的不滿足傅里葉變換絕對值可積的條件,嚴格意義傅里葉變換不存在,于是發明了自相關函數的概念,將信號的蘊含的周期信號識別出來,并將相位信息去掉(相位不影響平均功率),于是就出現了我們在教材上見到的最終形式維納-辛欽定理:一個信號的功率密度譜,就是其自相關函數的傅里葉變換。提煉一下就是:隨機信號→幅值正太分布→均方值(平均功率)→帕斯瓦定理(功率守恒)→自相關函數(去除相位信息)→維納-辛欽定理(最終形式)。
免責聲明:本文為轉載文章,轉載此文目的在于傳遞更多信息,版權歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權問題,請聯系小編進行處理。







