【導讀】我們在前文講述電壓駐波比的文章中提到過傳輸線的狀態,即完全匹配狀態,完全反射狀態和部分比配狀態。我們知道,完全匹配狀態下,是不存在駐波的,即駐波比 VSWR 為 1. 完全反射狀態下,會形成純駐波,電壓駐波比 VSWR 為無窮大。
我們在前文講述電壓駐波比的文章中提到過傳輸線的狀態,即完全匹配狀態,完全反射狀態和部分比配狀態。我們知道,完全匹配狀態下,是不存在駐波的,即駐波比 VSWR 為 1. 完全反射狀態下,會形成純駐波,電壓駐波比 VSWR 為無窮大。實際系統設計中,最為常用的是部分匹配,即我們要根據系統的駐波比要求去完成實際系統的設計。
今天,我們來看一個極限——傳輸線的全反射狀態——即純駐波條件下的傳輸線特性。
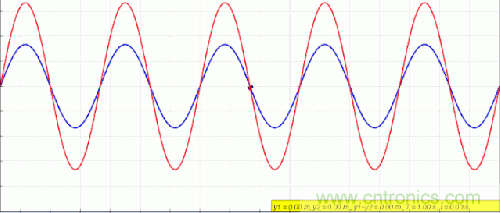
看上圖可以看出,純駐波是一個穩態,這個穩態在我們的射頻電路設計中是不是也是由它的獨特用處呢?下面我們慢慢說。
在一個無耗傳輸線中,當終端短路,開路或者接純電抗負載時,到達傳輸線終端的電磁波不能被吸收,將會全部反射回去,形成與入社比等輻的反射波,如上圖中的藍線所示。這種工作狀態就是全反射狀態。
傳輸線的電壓和電流方程
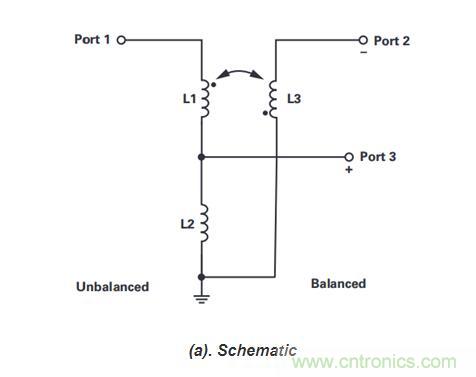
這里分三種情況去分析全反射狀態下的傳輸線特性。
No.1 終端短路
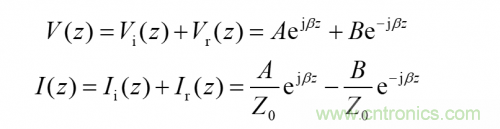
當傳輸線的終端接短路負載時,ZL=0,在負載處電壓 VL=0,這種情況下,負載處的入射波和反射波電壓等幅反向,即
這樣在整個傳輸線上的電壓和電流都是由等幅的入射波和反射波疊加而成的。將上面的 A 和 B 帶入傳輸線的電壓電流方程,可得:
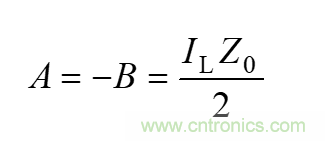
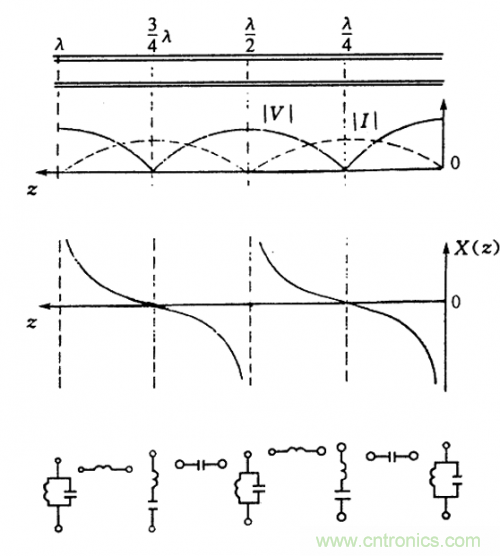
通過上式可以得出短路傳輸線上的電壓和電流分布圖。在負載 z=0 處,反射波電壓和入射波電壓等幅反向,故合成波的電壓振幅為 0,由于反射波電流和入射波電流等幅同相,合成波電流的振幅最大為入射波振幅的兩倍。合成波電壓的振幅沿傳輸線按正弦函數的規律分布,合成波電流的振幅則沿傳輸線按照余弦函數的規律分布。
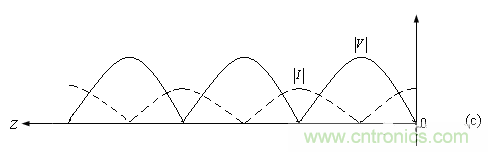
這里就引出了駐波的概念,我們在重復一遍。由兩個方向傳輸的電磁波相互疊加而形成的振幅起伏分布的合成波就是駐波。同向疊加的振幅最大的地方解釋波腹,其實就是波肚子;反向抵消的振幅最小的地方就是波節。由等輻反向的入射波和反射波相互疊加形成的就是純駐波。純駐波波節點處振幅最小為 0,波腹振幅為入射波或者反射波的兩倍。
可見由全反射狀態形成的駐波就是純駐波。因此全反射狀態又稱為純駐波狀態。根據正弦函數 / 余弦函數的定義,我們知道,在 z=0,z=波長 /2,...,z=n/2(波長),為電壓的波節點,電流的波腹點。在 z=波長 /4,...,z=(2n-1)波長 /4 處,為電壓波腹點,電流波節點。
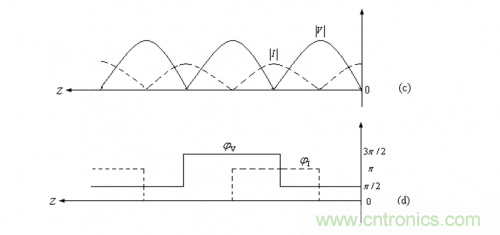
在終端短路的傳輸線上,任何觀察點的電壓和電流的相位差為 90°。因此,在整個傳輸線上,純駐波電壓達到最大值的瞬間,純駐波電流為 0,反之,當純駐波電流為 0 時,純駐波電流最大。也就是說,在整個傳輸線上,電壓和電流交替到達波節或者波腹的時間間隔為 1/4 周期。相位分布如上圖所示。相鄰波節點之間的相位相同,在波節點兩側相位差 180°。
重點來了。。。先看圖,在說明。
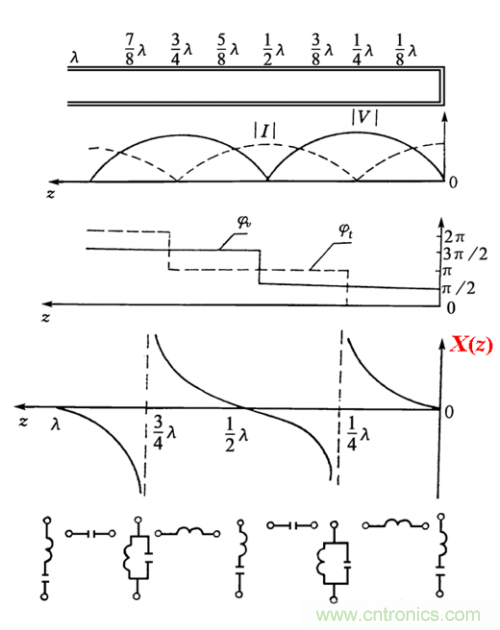
終端短路的無耗傳輸線上等效電抗 X(z)分布曲線如上圖第四幅圖所示,由圖可見,在負載處,阻抗為 0,故可等效為串聯諧振回路;在 0<z<波長 /4 處等效阻抗成感性,可等效為電感;在 z=波長 /4 處,等效阻抗為無窮大,可等效為并聯 LC 諧振回路;在波長 /4<z<波長 /2 處,等效阻抗為容性,可等效為電容。等效阻抗在整個傳輸線上的分布具有波長 /2 的周期性分布。
No.2 終端開路
無耗傳輸線終端開路時,負載阻抗 ZL=無窮大,因此在負載處,電流 IL=0,這種情況下入射波和反射波電壓的振幅等幅同相。即:
A=B=VL/2
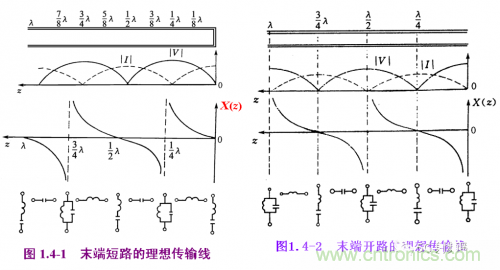
經過同樣的分析過程可得到終端開路傳輸線上的電壓,電流振幅分布和等效電抗分布特性。
對比上圖終端短路傳輸線的等效電抗分布圖,您發現了什么?
為了對比方便我們把兩幅圖合在一起。分布規律相同,但是相差了波長 /4. 也就是說,終端短路傳輸線移動四分之一波長就成了開路,反之,終端開路的傳輸線移動四分之一波長就成了短路。工程中也常常用到這種替代方式哦
No.3 終端接純電抗負載
我們知道,純電抗負載,對于電磁波來說,也就是影響了相位,那很明顯,我們把這段相位的傳輸線挪走不就等效成了終端短路或者終端開路?
推導過程省略 500 字。直接上圖。
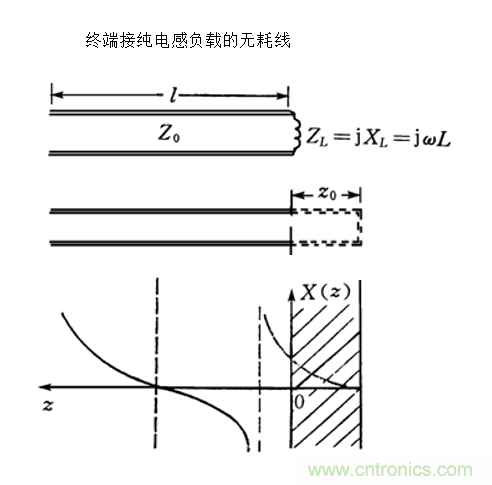
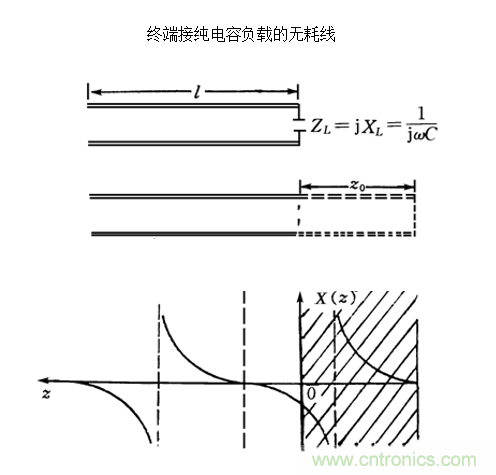
終端接純電抗負載的無耗線上的電壓、電流振幅分布與終端短路傳輸線的相同,只是起點不同而已。
全反射特性:
1,無耗傳輸線上反射波與入射波等輻,電壓駐波比為無窮大。
2,從負載處開始,等效阻抗依次為:等效短路,等效電感,等效開路,等效電容。。。。。負載不同,起始點不同。
3,整個傳輸線上沒有行波分布,都是純駐波。
4,相鄰兩個波節點相位相同,波節點左右兩側相位差 180°。
5,同一點處電壓和電流相位相差 90°,沒有能量傳輸,只有電場和磁場的能量交換。
這不就是我們所說的諧振嗎?
最后我們看一個問題
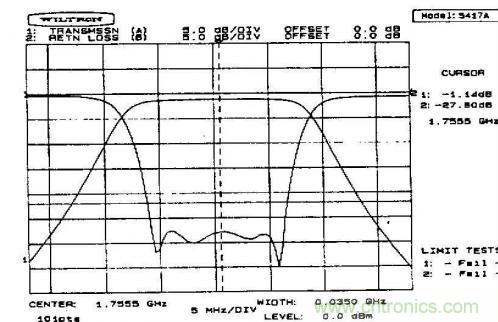
濾波器是一個帶寬一定的匹配網絡,那么帶外信號就反射回去了,這個濾波器帶外等效為開路還是短路呢?
免責聲明:本文為轉載文章,轉載此文目的在于傳遞更多信息,版權歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權問題,請聯系小編進行處理。






