【導讀】幾個關鍵的系統性能指標由對應于幅度和相位的正交輸入參數確定;兩個例子是正交調制器載波饋通和邊帶抑制。這些參數通過優化 DC 偏移平衡以及調制器正交基帶輸入之間的振幅和相位平衡得到改善。
幾個關鍵的系統性能指標由對應于幅度和相位的正交輸入參數確定;兩個例子是正交調制器載波饋通和邊帶抑制。這些參數通過優化 DC 偏移平衡以及調制器正交基帶輸入之間的振幅和相位平衡得到改善。
由于在給定二維空間的情況下找到這些參數的調整點并不是一項微不足道的任務,因此在本文中我將討論一種 Python 算法,用于在具有正交輸入向量的二維空間中找到調整點。該算法基于測量數據點求解相交圓的方程,并在短短四次迭代中找到點。為了舉例說明該技術,我使用了德州儀器 (TI) AFE7070集成數模轉換器 (DAC) 以及正交調制器載波饋通參數。
優化雜散發射
通信系統努力將雜散發射降至。其中一些雜散發射源自正交輸入信號失配。例如,直流偏移失配和幅度/相位失衡將分別影響模擬正交調制器中的載波饋通和邊帶抑制參數。將輸入變量調整到設定點可限度地減少雜散輸出。
圖 1 將測量參數表示為從優化點 [x0,y0] 到二維平面上的實際點的矢量的大小 (r)。參數值以單位圓[0,1]為界。0 表示完全取消或沒有信號,1 表示沒有取消或完全信號。在分貝標度中,該函數受 [-inf,0] 約束。半徑為 r 的圓代表所有可能達到相同大小的 x,y 點。
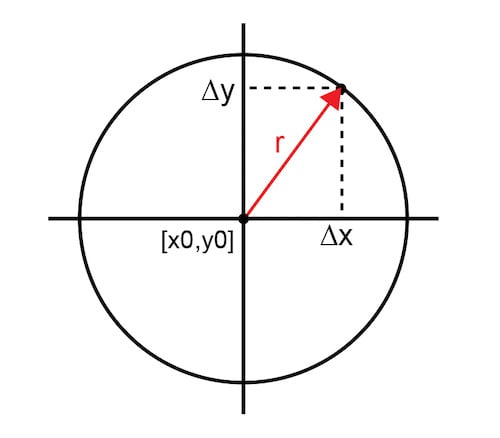
圖 1 優化點到實際點的向量
等式 1 以簡單的形式表示函數:
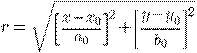 (1)
(1)
常數 [a0,b0] 表示系統相關的歸一化因子,以保持結果小于 1。從技術上講,等式 1 描述了一個橢圓,因為每個獨立變量的比例因子不需要相同。為簡化此分析,a0 等于 b0,因此曲線是真正的圓。
目標是盡快找到化測量參數 (r) 的點 [x0,y0]。使用統計上不同的輸入參數有效地找到該點具有挑戰性。傳統的狩獵和啄食方法使用連續試驗來縮小到點。雖然這會產生所需的解決方案,但在收斂時間很關鍵時需要太多迭代,因此需要一種新方法。
相交圓
理想情況下,恰好三個使用相交圓的測量迭代確定點。任意輸入點 [x1,y1] 處的個測量結果定義了由半徑為 r1 的圓 A 表示的點的無限可能性。添加第二個數據點會產生另一個無限數據集,由圓 B 表示;但是,兩個圓圈的交點將解決方案縮小為兩點。第三個數據點和相應的圓 C 提供了第三條曲線,其中只有一個相互交點。該交點是點。圖 2 顯示了以終點結束的相交圓的進展。
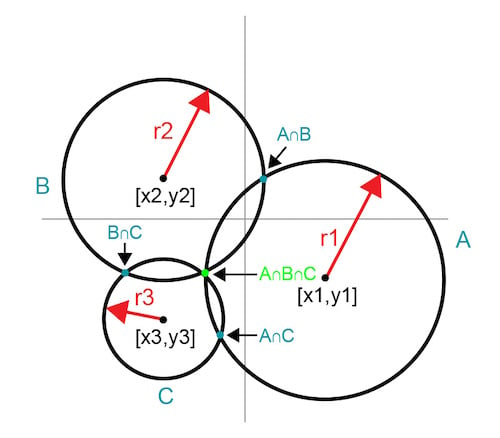
圖 2. 相交的圓揭示了一個共同的交點
該技術恰好在三次迭代中揭示了點。第四次迭代測量點以確認和記錄結果。
圖 3 說明了一種通過使用 xy 平面中的經驗已知邊界信息來消除迭代的技術。選擇其中一個邊界點的初始點,使條曲線 (A) 為 90 度弧。通過在 x 或 y 方向上移動來選擇個圓弧上的第二個點。
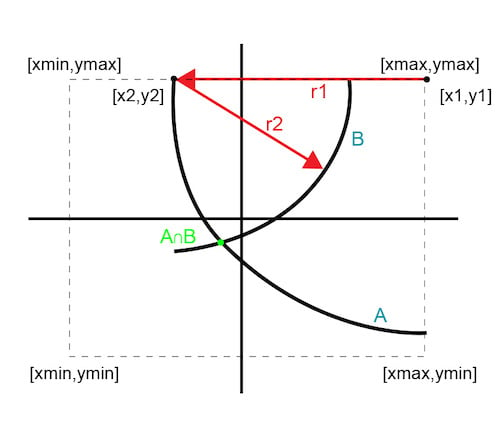
圖 3. 兩次迭代解決方案
由于第二個點仍在邊界邊緣上,因此它的曲線是一個小于 180 度的圓弧。這兩條曲線的交點提供了一個點。這種方法僅在兩次迭代中就揭示了點,并通過三次迭代對其進行了確認。
逐次圓近似
解決方案取決于數學方程式的準確性。在實際測量情況下,一些假設或錯誤會影響結果。測得的信號很小;噪聲和測量公差會引入誤差。使用完美的圓而不是橢圓會帶來一些不確定性。求解多個方程所需的比例因子假設也引入了不確定性。這些錯誤和假設轉化為曲線的模糊性。
圖 4 說明了模糊曲線如何不能保證的交點;相反,它們定義了一個融合區域。
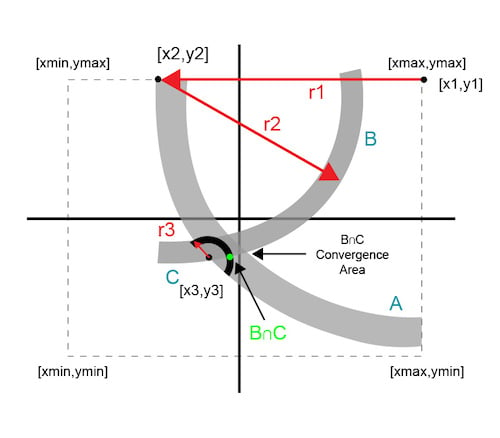
圖 4. 逐次圓相交近似
每個額外的數據點都使用上迭代的數據。連續的圓圈會聚到系統閾值內的解決方案區域。
測量示例
該示例使用 AFE7070 DAC 并針對載波饋通參數進行了優化。AFE7070 是一個方便的平臺,因為 DAC 和調制器集成在一起。調制器正交輸入端的直流偏移不平衡決定了載波饋通性能。AFE7070 具有內部數字調諧功能,可控制直流偏移平衡。不需要太多;分辨率為微伏級。
該示例的 x,y 參數是整數數字步進值,用于控制正交輸入上的直流電平。設備的先前統計抽樣提供了輸入變量的 x、y 邊界以及計算中使用的步驟表。步驟表提供了以分貝毫瓦為單位的測量載波饋通到 delta-x(或 delta-y)因子的“轉換”。
高(或換句話說,差)測量值意味著設置偏離,需要更大的增量才能達到點。相反,較低的值意味著設定點很接近并且需要小幅修正。這點“功課”是必要的,以確保初始猜測點不會太遠,并將迭代時間減少到限度。
圖 5 顯示了在四次或更少的迭代中找到輸入變量的 Python 算法。
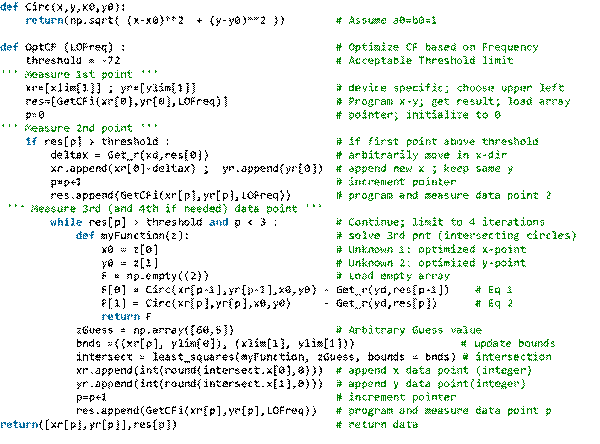
圖 5. Python 優化算法
函數“Get_r”和“GetCFi”是特定于設備的測量。為簡潔起見,我省略了代碼,因為它對于演示優化算法無關緊要。在您的應用中,這些功能與系統中設備參數的編程和測量有關。
結論
對于 AFE7070 DAC,在大多數情況下,該算法在三次迭代內優化載波饋通,耗時不到 1.7 秒,主要由頻譜分析儀穩定和掃描時間控制。以前的步驟方法需要近 20 次迭代和 20 多秒才能完成。與傳統方法相比,該算法的速度提高了 10 倍以上。依賴于增益和相位的正交輸入變量的其他通信系統參數也可以使用該算法有效地找到解決方案。
免責聲明:本文為轉載文章,轉載此文目的在于傳遞更多信息,版權歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權問題,請聯系小編進行處理。
推薦閱讀:






