【導讀】電感位移傳感器被廣泛應用于微小位移量檢測中,但在一些工程中現有傳感器的測量精度和靈敏度達不到測量要求。針對這一問題,對傳感器前段信號處理電路進行改進,在傳感器上下線圈并聯電容形成LC電路,利用LC電路諧振效應改善電路的性能,以提高信號源頭的靈敏度;采用Multisim軟件對半橋和全橋電路在并聯不同大小的電容后的性能進行仿真,并用Matlab對生成的曲線進行最小二乘擬合,比較得出使電路性能最優的電容值和并聯方法。結果表明在損失微小線性度的情況下可將靈敏度提高一倍。
電感位移傳感器被廣泛應用于微小位移量檢測中,但在一些工程中現有傳感器的測量精度和靈敏度達不到測量要求。針對這一問題,對傳感器前段信號處理電路進行改進,在傳感器上下線圈并聯電容形成LC電路,利用LC電路諧振效應改善電路的性能,以提高信號源頭的靈敏度;采用Multisim軟件對半橋和全橋電路在并聯不同大小的電容后的性能進行仿真,并用Matlab對生成的曲線進行最小二乘擬合,比較得出使電路性能最優的電容值和并聯方法。結果表明在損失微小線性度的情況下可將靈敏度提高一倍。
電感位移傳感器的實質,是將敏感元件的變化量轉化成電壓幅值的變化量來進行測量,其廣泛應用于檢測微小位移量的檢測系統中,因此對電感傳感器的測量精度和靈敏度要求很高。電感位移傳感器的靈敏度是指輸出電壓的增量與側頭位移增量的比。在其他條件相同的情況下提高靈敏度可以提高系統的最小分辨率和精度。提高電感傳感器靈敏度的方式有多種,但目前主要都是通過對電感傳感器的信號調理電路的改進來實現。文中嘗試通過諧振電路改變傳感器的輸出信號,從信號源頭增大傳感器靈敏度。這種方法相當于對傳感器本身進行改進,使得它還可以與其他改進技術如:傳感器激勵源、輸出信號處理、計算機軟件補償等兼容以共同提高整個系統的性能。
1 改進后電路的模型建立
1.1 半橋式改進電路
如圖1如果沒有C1和C2為普通半橋電路,虛線框中為電感傳感器的等效電路,傳感器測頭的位移帶動螺線管中鐵芯上下移動,從而改變上下兩個線圈的電感值。將兩線圈等效成純電阻和純電感的串聯,如圖中R1和L1組成上線圈,R2和L2組成下線圈,輸出接在上線圈上。實際傳感器中線圈與輸出的接線不會變,只是通過鐵芯移動來改變電感,所以R1和R2固定不變。輸出電壓
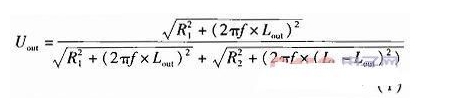
圖1在上下兩個線圈并聯電容C1和C2后,分別形成了諧振回路I和回路II。如果鐵芯在最下方時:回路II諧振,回路I失諧。當鐵芯在最上方時:回路I諧振,回路II失諧。由于諧振電路在諧振時的阻抗會遠大于失諧時的阻抗。可以定性地得出,鐵芯在最下方時Uout的幅值會比沒有電容小,在最上方時會比沒有電容時大,所以靈敏度會增大。但在最下方和最上方中間的變化情況,以及它的線性度則需要后邊仿真來確定。輸出電壓
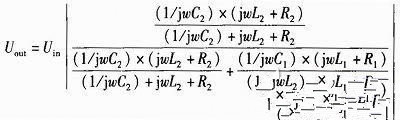
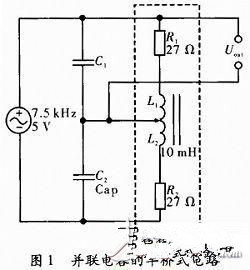
1.2 全橋式改進電路
普通全橋電路圖2(a),傳感器上下兩線圈分別與匹配電阻R3和R4相連,在L1=L2時電橋平衡,當向上發生△X的位移時,鐵芯上移,L1增大△L,L2減小△L,Uout的變化會比半橋方式增加近兩倍,輸出電壓
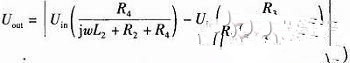
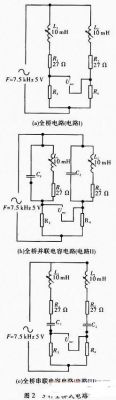
如圖2(b)和圖2(c)對上下兩線圈分別采用并聯和串聯電容C1和C2的方式,形成諧振回路I和回路II,通過后續仿真觀察這兩種方式電路性能的變化情況。輸出電壓
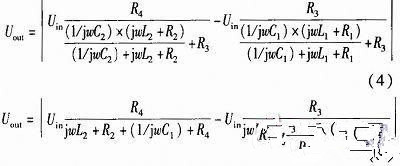
2 電路的仿真
2.1 仿真平臺及仿真條件
仿真平臺使用MulTIsim,它是美國國家儀器(NI)有限公司推出的以Windows為基礎的仿真工具,適用于板級的模擬/數字電路板的設計工作。它包含了電路原理圖的圖形輸入、電路硬件描述語言輸入方式,具有龐大的元器件庫和全面的儀器儀表庫和豐富的仿真分析能力。采用它來對改進前后的電路進行仿真。
在仿真之前,先結合工程實際情況對仿真條件進行一些設定:
(1)激勵電源:頻率為7.5 kHz,峰峰值為5 V的交流電。
(2)傳感器:總電感值為10mH差動電感傳感器,線性范圍為3~7mH,電感的自身的電阻值為54Ω。
如上文所述R1和R2固定不變,所以R1和R2為27Ω。而對應的純電感L1和L2,會隨著位移線行變化,滿足L1+L2=10 mH(3《L1《7,3《L2《7)。
2.2 仿真過程及結果
對于半橋時電路II由于希望鐵芯在最下方時回路II諧振,最上方時回路I諧振,因為L1和L2的變化范圍為3~7 mH。L2為7 mH時回路II諧振,L1為7 mH時回路I諧振。按照仿真條件計算C1=C2=65 nF。簡化仿真不妨取C1=C2,在65 nF附近從55~100 nF間隔5 nF進行仿真,觀察電路性能,仿真結果如圖3所示。
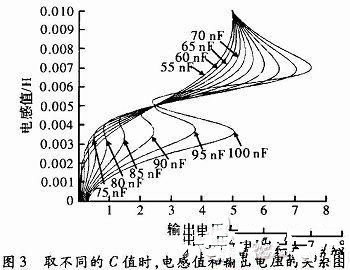
圖中可以看出不同的電容值對電路的性能影響很大,如果選擇不恰當,反而會使系統性能下降。只有選擇適當容量的電容大小才能使測量靈敏度提高,同時保持盡量小的線性誤差。所以選取曲線在L1=3~7 mH段時,靈敏度最高,線性度最好,進行最小二乘計算,它與普通半橋的對比如圖4所示。
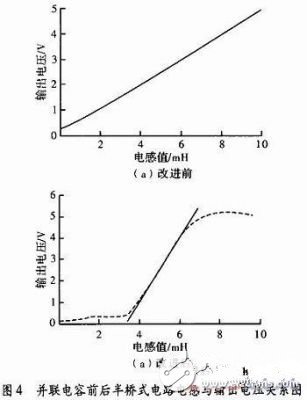
經Matlab計算普通半橋在3~7 mH段,電壓變化范圍1.5~3.5 V,電壓對電感的靈敏度為0.5V/mH。線性度近似為1。對圖4(b)采用最小二乘法擬合直線后,在3.8~6.3 mH段,輸出電壓的變化范圍0.77~4.39 V。線性度可達2.39%,靈敏度為1.448 V/mH。
對全橋電路的仿真與半橋的方法類似,需要注意的是希望電橋在L1=L2=5 mL時平衡,所以對于匹配電阻的選取需要根據仿真條件計算
對于電路I:R3=R4=|jw×0.005+R1|=237 Ω;電路II:R3=R4=|(jwL+R1)∥(1/jwC1)|=817Ω;電路III:R3=R4=|jwL+R1+(1/jwC1)|=98Ω。
對于使用電容的電路,同樣對不同的電容值條件下的電路進行仿真,選出性能最好的如圖5所示。
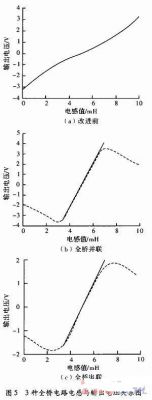
普通全橋在3.8~6.3 mH段,電壓變化范圍為-1.2~+1.3 V,電壓對電感的靈敏度為1 V/mH。線性度近似為1.38。對圖5(b)和圖5(c)使用Matlab進行最小擬合直線如圖所示,在3.8~6.3 mH段,并聯方式輸出電壓的變化范圍為-2.66~+2.66V,靈敏度為2.130V/mH線性度可達1.68%。串聯方式的輸出電壓范圍約為-1.25~+1.25V,靈敏度約為2.130V/mH線性度可達1.33%。
3 分析與結論
如表1所示,為各電路的靈敏度和線性度,可以在損失較小線性度條件下,將靈敏度提高。對于半橋雖然將靈敏度提高了近200%,但犧牲的線性度較大。串聯電容的方式靈敏度幾乎沒有增大。性能最好的是并聯電容后的全橋電路,靈敏度提升了113%,且損失的線性度較小,只比原來增大21.7%,而且實際應用中,可以通過軟件補償和事先標定來彌補線性度的不足。
如何提高電感傳感器的測量精度和靈敏度
綜合理論分析和仿真結果,在激勵源確定和電感傳感器參數確定的情況下,通過計算可以得到一個恰當的電容值,當在傳感器的兩部分線圈上并聯這個電容時,測量的靈敏度會有顯著提高,同時仍可以保持較好的線性度,從而達到改善和提高電感傳感器性能和最小分辨率的目的。
免責聲明:本文為轉載文章,轉載此文目的在于傳遞更多信息,版權歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權問題,請聯系小編進行處理。
推薦閱讀:






