【導(dǎo)讀】到目前為止,我們關(guān)注的是單層感知器,它由一個輸入層和一個輸出層組成。您可能還記得,我們使用術(shù)語“單層”是因為此配置僅包括一層計算活動節(jié)點,即通過求和然后應(yīng)用激活函數(shù)來修改數(shù)據(jù)的節(jié)點。輸入層中的節(jié)點只是分發(fā)數(shù)據(jù)。
到目前為止,我們關(guān)注的是單層感知器,它由一個輸入層和一個輸出層組成。您可能還記得,我們使用術(shù)語“單層”是因為此配置僅包括一層計算活動節(jié)點,即通過求和然后應(yīng)用激活函數(shù)來修改數(shù)據(jù)的節(jié)點。輸入層中的節(jié)點只是分發(fā)數(shù)據(jù)。
單層感知器在概念上很簡單,訓(xùn)練過程非常簡單。不幸的是,它不提供我們復(fù)雜的、現(xiàn)實生活中的應(yīng)用程序所需的功能。我的印象是,解釋單層感知器的基本限制的標(biāo)準(zhǔn)方法是使用布爾運算作為說明性示例,這就是我將在本文中采用的方法。
神經(jīng)網(wǎng)絡(luò)邏輯門
我們將使用一個極其復(fù)雜的微處理器來實現(xiàn)一個神經(jīng)網(wǎng)絡(luò),該神經(jīng)網(wǎng)絡(luò)可以完成與由少數(shù)晶體管組成的電路相同的事情,這個想法有些幽默。但與此同時,以這種方式思考這個問題強調(diào)了單層感知器作為一般分類和函數(shù)逼近工具的不足——如果我們的感知器不能復(fù)制單個邏輯門的行為,我們知道我們需要找到一個更好的感知器。
讓我們回到本系列篇文章中介紹的系統(tǒng)配置。
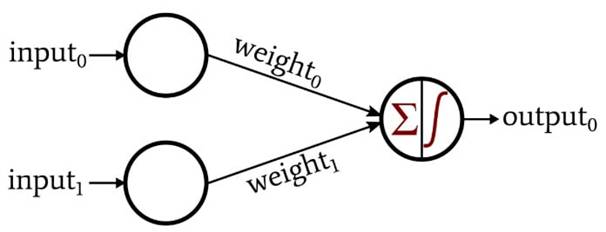
這個感知器的一般形狀讓我想起了一個邏輯門,事實上,它很快就會變成這樣。假設(shè)我們使用包含輸入向量元素的 0 和 1 的樣本來訓(xùn)練該網(wǎng)絡(luò),并且僅當(dāng)兩個輸入都等于 1 時輸出值才等于 1。結(jié)果將是一個神經(jīng)網(wǎng)絡(luò),它以類似于與門的電氣行為的方式對輸入向量進行分類。
該網(wǎng)絡(luò)輸入的維數(shù)為 2,因此我們可以輕松地將輸入樣本繪制成二維圖形。假設(shè) input0 對應(yīng)于水平軸,input1 對應(yīng)于垂直軸。四種可能的輸入組合將排列如下:
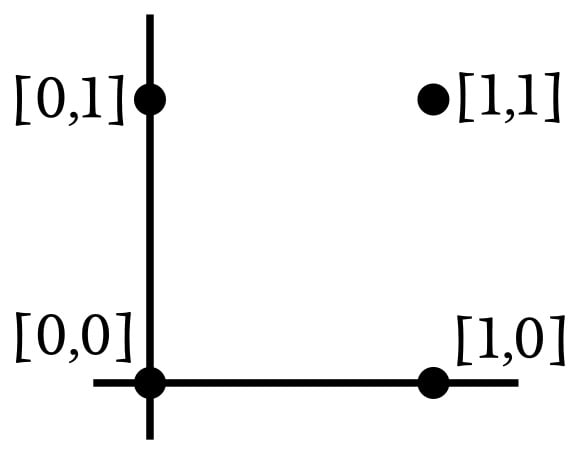
由于我們正在復(fù)制 AND 操作,因此網(wǎng)絡(luò)需要修改其權(quán)重,使輸入向量 [1,1] 的輸出為 1,其他三個輸入向量的輸出為 0。基于這些信息,讓我們將輸入空間劃分為對應(yīng)于所需輸出分類的部分:
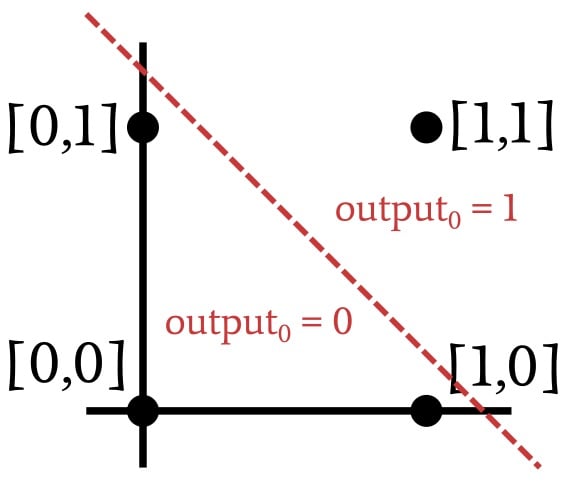
線性可分數(shù)據(jù)
如上圖所示,當(dāng)我們實現(xiàn) AND 運算時,可以通過繪制一條直線對繪制的輸入向量進行分類。線一側(cè)的所有內(nèi)容接收到的輸出值為 1,而另一側(cè)的所有內(nèi)容接收到的輸出值為零。因此,在 AND 運算的情況下,呈現(xiàn)給網(wǎng)絡(luò)的數(shù)據(jù)是線性可分的。OR 操作也是如此:
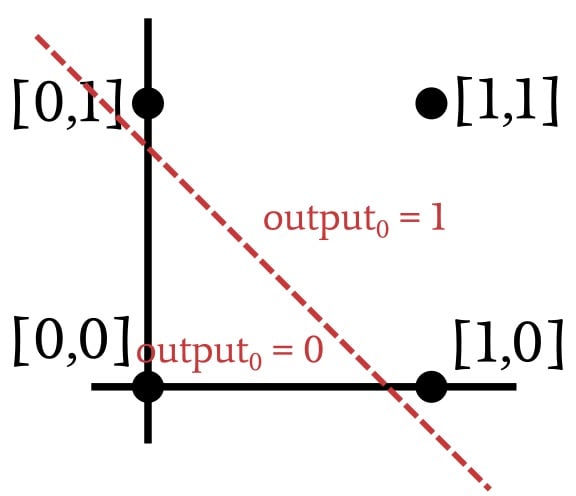
事實證明,單層感知器只有在數(shù)據(jù)線性可分的情況下才能解決問題。無論輸入樣本的維數(shù)如何,都是如此。二維情況很容易可視化,因為我們可以繪制點并用一條線將它們分開。為了概括線性可分性的概念,我們必須使用“超平面”這個詞而不是“線”。超平面是在n維空間中可以分離數(shù)據(jù)的幾何特征。在二維環(huán)境中,超平面是一維特征(即一條線)。在三維環(huán)境中,超平面是一個普通的二維平面。在n維環(huán)境中,超平面具有 ( n -1) 維。
解決不可線性分離的問題
在訓(xùn)練過程中,單層感知器使用訓(xùn)練樣本來確定分類超平面的位置。在找到能夠可靠地將數(shù)據(jù)分成正確的分類類別的超平面后,它就可以采取行動了。然而,如果超平面不存在,感知器將不會找到它。讓我們看一個不可線性分離的輸入到輸出關(guān)系的例子:
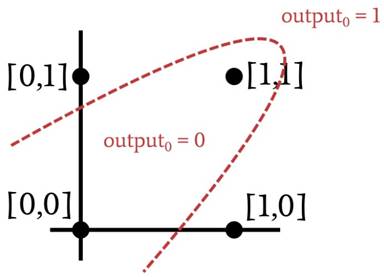
你承認這種關(guān)系嗎?再看一看,無非是異或運算。您不能用直線分隔 XOR 數(shù)據(jù)。因此,單層感知器無法實現(xiàn)異或門提供的功能,如果它無法執(zhí)行異或運算,我們可以放心地假設(shè)許多其他(更有趣的)應(yīng)用程序?qū)⒊鰡栴}的范圍 -解決單層感知器的能力。
幸運的是,我們可以通過簡單地增加一層額外的節(jié)點來大大提高神經(jīng)網(wǎng)絡(luò)解決問題的能力。這將單層感知器變成了多層感知器 (MLP)。正如上一篇文章所提到的,這一層之所以被稱為“隱藏”,是因為它與外界沒有直接的接口。我想您可以將 MLP 視為眾所周知的“黑匣子”,它接受輸入數(shù)據(jù)、執(zhí)行神秘的數(shù)學(xué)運算并生成輸出數(shù)據(jù)。隱藏層在那個黑盒子里面。你看不到它,但它就在那里。
免責(zé)聲明:本文為轉(zhuǎn)載文章,轉(zhuǎn)載此文目的在于傳遞更多信息,版權(quán)歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權(quán)問題,請聯(lián)系小編進行處理。
推薦閱讀:
霍爾效應(yīng)位置感測:滑動配置的響應(yīng)線性度和斜率
汽車LiDAR GaN的Design Win——高效功率轉(zhuǎn)換引領(lǐng)市場






