中心議題:
- 信號的矢量表示方法
- 頻譜儀數字中頻處理技術
- 信號解調方法
- 實時頻譜分析
- 雷達信號測試分析
- 發射機和頻綜源穩定時間測量
隨著現代頻譜儀數字中頻處理技術的發展和應用,使其在通信、航天、計量以及軍工各個領域中的使用愈加廣泛。不僅使數字信號解調成為可能,并且為模擬調制信號的解調提供的更優秀的方法。同時,對于發射機和頻綜源的頻率及相位穩定時間,也可以進行精確的分析。
信號的矢量表述方法
理解信號的矢量表達以及IQ信號的概念,是現代頻譜分析和信號分析理解和應用的基礎。作為一個圖解工具,矢量是一個直角坐標系中的旋轉的箭頭。箭頭的長度代表信號的峰值幅度。逆時針旋轉方向為正方向。箭頭與橫軸正半軸的夾角為相位。信號周期對應于箭頭旋轉一周的時間。信號每秒鐘完成旋轉的次數對應于信號頻率。
信號矢量在縱軸上的投影長度等于信號的峰值幅度乘以相位正弦值,因此,如果信號是一個正弦波,該投影就對應于信號的瞬時幅度(見圖1)。
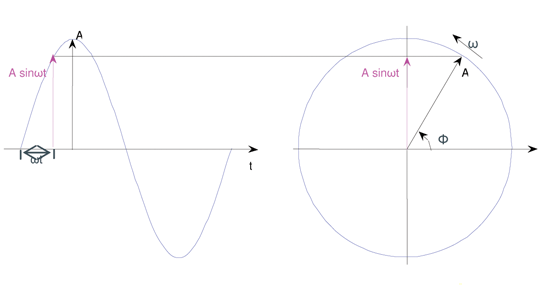
圖1 時域表述的正弦波與矢量信號的對應關系
用矢量表述信號,可以完整地描述信號的幅度、頻率和相位。因此,在信號分析中,我們常把信號進行矢量分解,也就是將信號分解為頻率相同、峰值幅度相同但相位相差90的兩個分量。通常,我們采用一個正弦信號(Asinwt)和一個余弦信號(Acoswt)描述這兩個分量,其中余弦分量被稱為同相分量,即I分量;正弦分量被稱為正交分量,即Q分量。
頻譜儀數字中頻處理技術
輸入頻譜儀的射頻信號經過混頻后變為中頻信號IF,再經過帶通濾波器(中頻濾波器)進入A/D轉換器。在數字處理部分,對下變頻為基帶的IQ信號進行低通濾波和欠采樣,存儲在內存中,準備進一步處理,存儲的數據表述IQ信號的電壓值。
在頻譜儀設置過程中,模擬中頻濾波器帶寬為IFBW,數字處理部分的低通濾波器帶寬為解調帶寬。欠采樣使IQ信號的采樣率除以2的n次方,當解調帶寬較窄時,過高的采樣速率是毫無意義的。
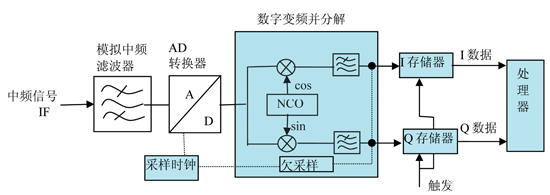
圖2 頻譜儀中頻信號處理原理圖
[page]
信號解調方法
對應內存中的IQ信號,可以采用的處理方法有:幅度分析、頻率分析、相位分析和FFT頻譜分析。在頻譜儀的矢量分析過程中,頻譜儀設置為零SPAN,也就是在固定輸入頻率處,中頻帶寬之內進行分析。
1.分析處理
![]() (1)
(1)
其中,Am為輸入信號的幅度。根據IQ信號的每一個采樣值,可以計算出對應采樣時刻的幅度值,顯示單位可以是線性電壓值 (V), 對數電壓 (dBmV) 或功率值(dBm)。在測量時間內的所有Am數值構成IQ幅度數組Am-DC。
![]() (2)
(2)
其中,Φm為輸入信號的相位。根據IQ信號的每一個采樣值,可以計算出對應采樣時刻的相對相位值。在測量時間內的所有Φm數值構成IQ幅度數組Φm-DC。
![]() (3)
(3)
其中,Fm為輸入信號的頻率。對相鄰點相位差值對時間求導,得出頻率值。在測量時間內的所有Fm數值構成IQ幅度數組Fm-DC。
![]() (4)
(4)
其中,Spec為輸入信號中頻帶寬內的頻譜。
2. 解調方法
如前所述,對應于載波信號,可以得到隨時間變化的幅度、相位和頻率曲線以及實時頻譜。
2.1 AM解調
對AM-DC數組進行分析,此數組對應射頻功率-時間曲線TRF。
對此數組進行FFT計算,得到AF頻譜,其基波頻率即調制頻率fmod ,根據AF頻譜,可以計算調制諧波失真和信納比。
對此數組進行窄帶低通濾波,獲得載波幅度數組Vc ,計算AM-DC與Vc的差分數組,它與Vc的比值AMdeep 數組表述調制深度,對其進行檢波:正峰值 (+pk):數組中的最大值;負峰值 (+pk):數組中的最小值;峰-峰值/2 (1/2pk-pk):數組中的最大值與最小值差值的一半;均方根值 (rms):數組中數值的均方根值。
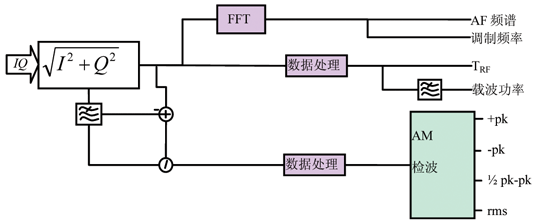
圖3 AM解調原理
2.2 FM解調
對FM-DC數組進行分析,此數組對應頻率曲線TFM 。
對此數組進行FFT計算,得到AF頻譜,其基波頻率即調制頻率fmod ,根據AF頻譜,可以計算調制諧波失真和信納比;
對此數組進行檢波,與AM解調類似,獲得峰值和均方根值。
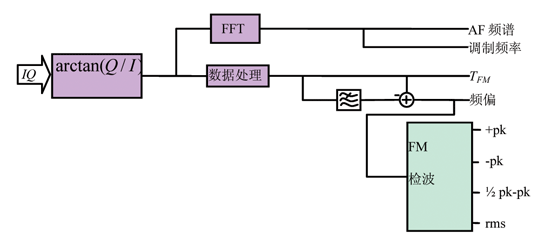
圖4 FM解調原理
[page]
2.3 ΦM解調
對ΦM-DC數組進行分析,此數組對應頻率曲線ΦFM 。
對此數組進行FFT計算,得到AF頻譜,其基波頻率即調制頻率fmod ,根據AF頻譜,可以計算調制諧波失真和信納比。
對此數組進行檢波,與AM解調類似,獲得峰值和均方根值。
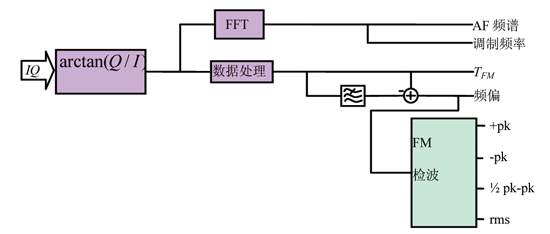
圖5 ΦM解調原理
2.4 FM解調實例
圖6是羅德與施瓦茨公司頻譜儀選件FS-K7在分析調頻信號的應用。它采用上述解調原理,可以實時解調調頻、調幅、調相和實時頻譜。
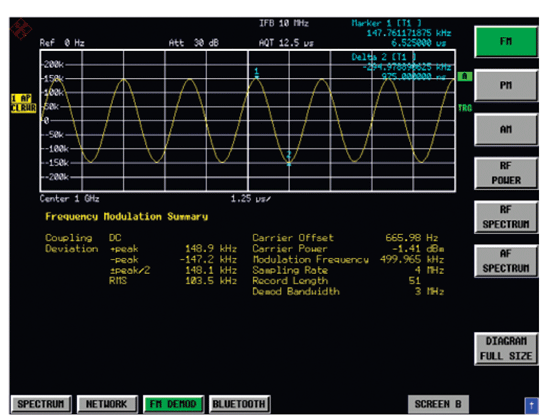
圖6 FM解調分析
實時頻譜分析
實時頻譜分析與傳統的頻譜儀分析技術不同,是在傳統超外差式頻譜儀的基礎上,對中頻信號進行FFT分析(見公式4)。由于其實時快速的特點,在現代通信與雷達信號的分析中,尤其是跳頻信號的監測,得到越來越多的應用。
實時頻譜分析同時包含AF頻譜監測,分析AM或RF power的解調頻譜,有助于分析未知信號的符號速率。對應于非等幅連續數字調制信號(如PSK、QAM信號),在AF頻譜上,大于0Hz的第一個峰值點通常對應于信號的符號速率,使未知信號的矢量分析成為可能。
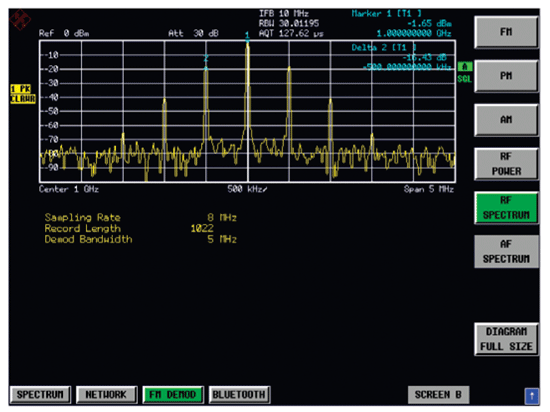
圖7 實時頻譜分析
[page]
雷達信號測試分析
由于頻譜儀的矢量分析功能可以實時分析信號的頻率、功率、相位和實時頻譜,因此在現代雷達的研發和測試之中,具有矢量分析功能的頻譜儀已經成為雷達發射機及其器件的必備工具。
雷達信號分析原理與“信號解調方法”一致,分析幅度、頻率和相位在時域內的特性曲線。對于常用雷達信號,如線性調頻,巴克碼等,可以分析它們的脈內特性,包括升降沿分析、頻率特性、相位特性以及矢量圖等。
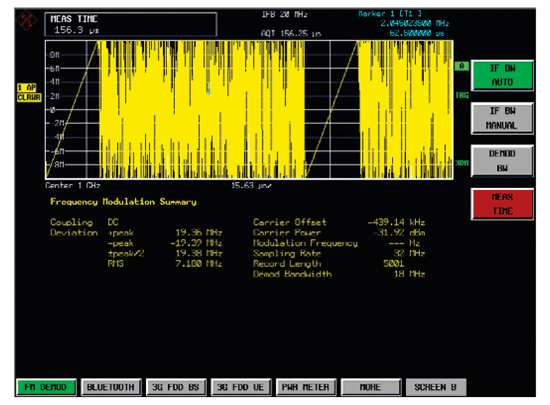
圖8 線性調頻信號分析
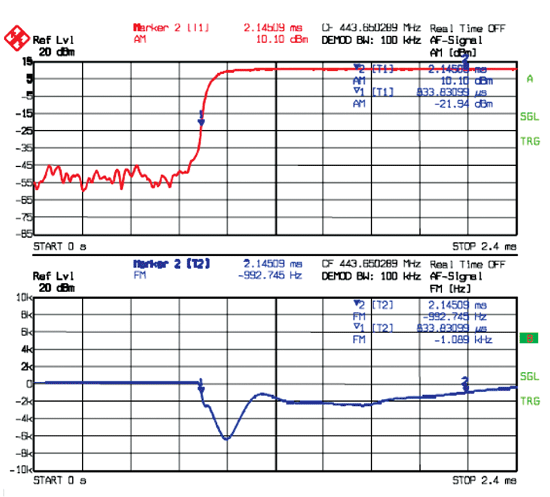
圖9 瞬態特性測試
雷達信號測試分為功率和頻譜測試以及脈內調制測試。圖8所示為線性調頻脈內調制測試,觀察脈內頻率變化情況,包括線性度和調頻帶寬,采用頻譜儀的矢量分析功能。在頻譜儀基本頻譜分析功能的頻域測試,可以觀察信號頻譜以及測試功率,頻譜儀時域測試或矢量分析的AM解調,可以測試脈沖波形、升降沿等信息。
發射機和頻綜源穩定時間測量
對于發射機和頻綜源來說,它們的幅度、頻率和相位瞬態特性是重要的測試指標。一般來說,頻率穩定時間是指發射機在輸出電平達到一定數值(通常為穩定輸出功率-30dB)開始,監測FM解調頻譜,直到頻率穩定到設計限值之內的這一段時間。
其分析原理與前文“信號解調方法”一致,分析幅度、頻率和相位在時域內的特性曲線,用AM曲線定義起始時間,觀察FM和PM曲線,獲得測試結果。
結語
在現代頻譜分析技術中,矢量分析技術是及其重要的一環,具有廣闊的發展和應用前景。同時,這也是解調分析中必不可少的手段,適用于各種模擬和數字調制信號的解調,包括一些特殊調制信號如應用在航空系統的VOR/ILS等。在通信信號解調分析(模擬和數字)、雷達信號分析以及頻綜瞬態分析等領域,矢量信號分析的應用在不斷發展和創新。







