【導讀】如果采用網格節點(mesh-node)分析能很好地求解電路的傳遞函數,那么立即獲得一個有意義的符號公式通常是不可能的,需要額外的工作才能得出。應用經典的分析技術來獲得所謂的低熵表達式–即分數形式,從中您可識別增益、極點和零點–往往導致如Middlebrook博士曾在他的文獻[1]、[2]中提到的代數失效(algebraic paralysis)。
在此,快速分析電路技術(FACTs)可幫助您基于您在大學里學到的東西而擴展,以大大簡化分析。通過使用FACTs,不僅加快您的執行速度,而且最終結果將以有序的多項式形式出現,通常無需進一步的因子分解工作[3]、[4]。
本文首先介紹后文用于確定開關轉換器的控制到輸出傳遞函數的FACTs。這個主題很大,在此我們只談及表面,希望激勵您進一步挖掘這個主題。我們選擇了電壓模式耦合電感單端初級電感轉換器(SEPIC)工作于非連續導電模式(DCM)。PWM開關[5]將用于形成小信號模型。
01 快速分析技術(FACTs)簡介
FACTs背后的基本原理在于電路時間常數的確定–t=RC或t=L/R–此時在兩種不同的條件下觀察所研究的電路:當激勵信號降至0時和響應清零時。通過使用這種技術,您將體會到確定特定傳遞函數有多快和直觀。基于這種方法的分析技術始于幾十年前,如[6]和[7]中記載的。
傳遞函數是一種數學關系,它把激勵信號、激勵物,和由這種激勵產生的響應信號聯系起來。如果我們考慮一個線性時不變(LTI)系統無延時,具有靜態增益H0–例如開關轉換器的線性理想功率級-其連接控制信號Verr(激勵)和輸出Vout(響應)的傳遞函數H可表示為:
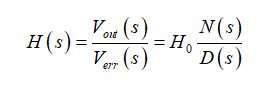 (1)
(1)首項H0是系統在s=0評估表現出的增益或衰減。該項將帶傳遞函數的單位(或維度),如果有的話。如果響應和激勵都用伏特表示,在此我們表示為Verr和Vout,H是沒有單位的。分子N(s)控制傳遞函數的零點。數學意義上,零點是函數幅值為零的根。通過FACTs,我們用數學抽象思維以輕松地揭開這些零點。我們不會像通常在諧波分析(s=jw)中所做的僅僅考慮在s平面的垂直軸,而是覆蓋考慮到負數根的整個平面。
因此,如果電路存在零點,將表現為當輸入信號調到零角頻率sz時無信號的輸出響應。在這種情況下,在變形的電路中的一些阻抗阻擋了信號傳播,響應為零,盡管存在激勵源:當變形的電路在s=sz點被激勵時,在信號路徑的串聯阻抗趨于無窮或分支將該激勵分流到地面。
請注意,這種方便的數學抽象通過觀察提供了巨大的幫助來找到零點,通常無需寫一行無源電路的代數。圖1提供了簡單的流程圖,詳細介紹了過程。關于這種方法的更多細節見[8]。
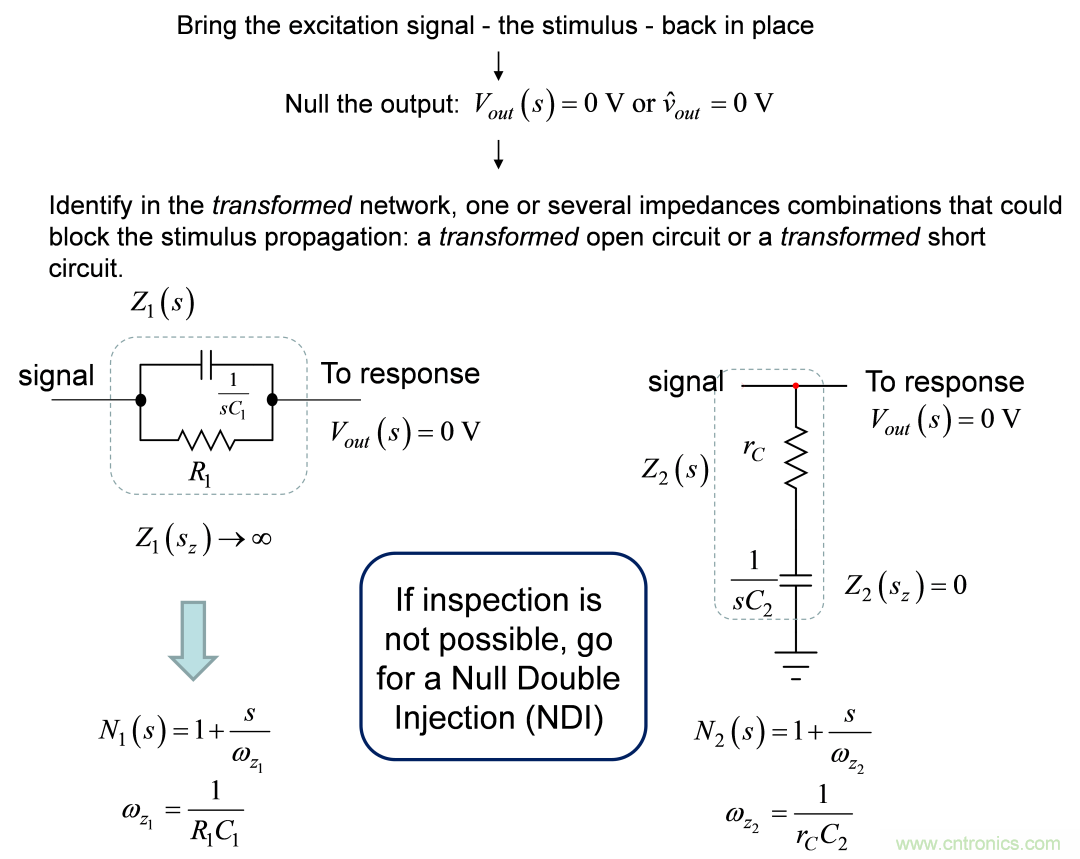
圖1:這個簡單的流程圖將指導您用最簡單的方法確定零點。在觀察無用時,您將需要進行雙重抵消注入或NDI。
翻譯參考▽
● Bring the excitation signal – the stimulus – back in place:將該激勵信號 – 激勵-帶回原處
● Null the output:將輸出清零
● Identify in the transformed network, one or several impedances combinations that could block the stimulus propagation: a ● transformed open circuit or a transformed short circuit.:在變形的電路中找到一個或一些可阻擋激勵傳播的阻抗組合:一個變形的開路電路或變形的短路電路
● Signal:信號
● To response : 到響應
● If inspection is not possible, go for a Null Double Injection(NDI):若觀察無用,則進行雙重抵消注入(NDI)
分母D(s)由電路自然時間常數構成。通過設置激勵信號為0和確定從電路中臨時移除的所考慮的電容或電感“所示”的阻抗,來得出這些時間常數。
通過“觀察”,您可想象把一個歐姆表置于暫時移除的儲能元件(C或L),并讀取它顯示的電阻。這其實是個相當簡單的運用,正如圖2中的第二個流程圖所詳述的。

圖2:該流程圖解釋了用于確定電路時間常數的方法。
翻譯參考▽
● Count energy-storing elements with independent state variables:計算具有獨立狀態變量的儲能元件
● Assume there are two energy-storing element, L1 and C2:假設有兩個儲能元件,L1和C2
● The denominator follow the form:分母遵循此公式
● Open the capacitor, short the inductor, determine the dc gain H0 if it exists:電容開路,電感短路,確定直流增益H0,若H0存在
● Reduce the excitation to 0 and determine time constants for b1 and b2:減小激勵至零,并確定b1和b2的時間常數
● Determine the resistance Ri driving LI while C2 is open circuited:確定驅動L1而C2 開路時的阻抗Ri
● Determine the resistance Rj driving C2 while LI is short circuited:確定驅動C2 而L1短路時的阻抗Rj
● Sum the time constants:將時間常數相加
● Determine the resistance Rk driving LI while C2 is short circuited:確定驅動L1而C2 短路時的阻抗Rk
● Determine the resistance Rl driving C2 while LI is open circuited:確定驅動C2 而L1開路時的阻抗Rl
● Choose the simplest combination:選擇最簡單的組合
看到圖3,是一個涉及注入源的一階無源電路—該激勵源—加偏壓于左邊網絡。輸入信號Vin通過網格和節點傳播,形成您看到的電阻R3上的響應Vout。我們感興趣的是導出連接Vout和Vin的傳遞函數G。
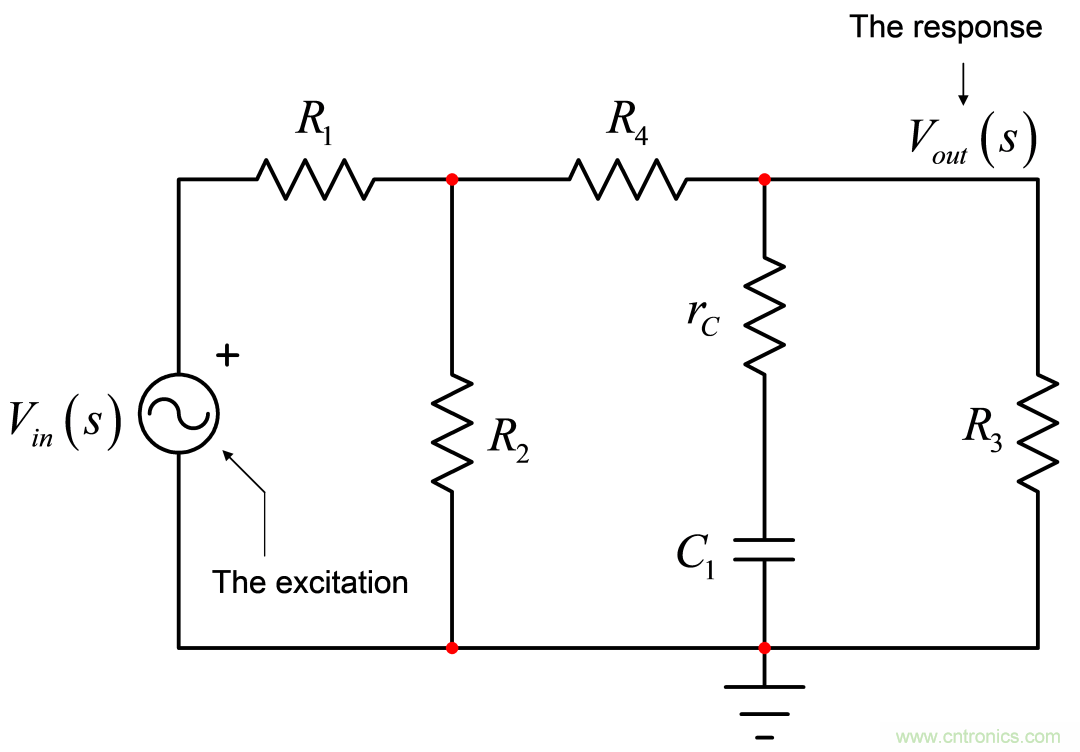
圖3:確定電路的時間常數需要將激勵源設為0,并看看從電路中暫時移除的能量存儲元件所提供的電阻。
翻譯參考▽
● The response:響應
為確定本例電路的時間常數,我們將激勵源設為0(由短路代替0V電壓源,開路代替0A電流源),拆下電容器。然后,我們連接一個歐姆表來確定電容器端提供的電阻。圖4指導您進行這些步驟。
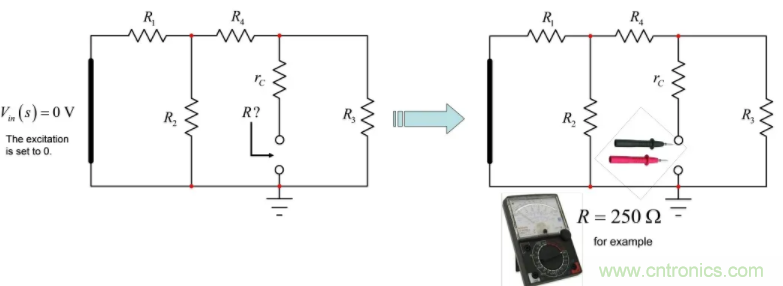
圖4:由短路代替0V源后確定電容器端的電阻。
翻譯參考▽
● The excitation is set to 0:激勵源設為零
● For example:例如
如果用圖4的做法,您“看到” R1與R2并聯后與R4串聯,所有這些與R3并聯后與rC串聯。該電路的時間常數只通過R和C1即可計算得出:
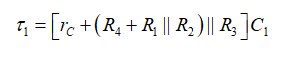 (2)
(2)我們可證明第一階系統的極點是其時間常數的倒數。因此:
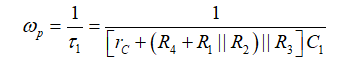 (3)
(3)現在,s=0時該電路的準靜態增益是多少?在直流條件下,電感器短路,電容器開路。把這概念應用于圖3的電路,繪制成如圖5所示。想象在R4前斷開連接,會看到一個含R1和R2的電阻分壓器。R2上的戴維寧(Thévenin)電壓為:
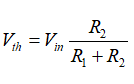 (4)
(4)輸出電阻Rth是R1與R2并聯的值。因此完整的傳遞函數涉及到電阻分壓器(由與Rth串聯的R4和加載的R3所構成)。rC是斷開的,由于電容C1在這直流分析中被移除。因此:
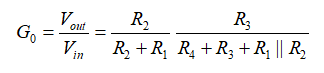 (5)
(5)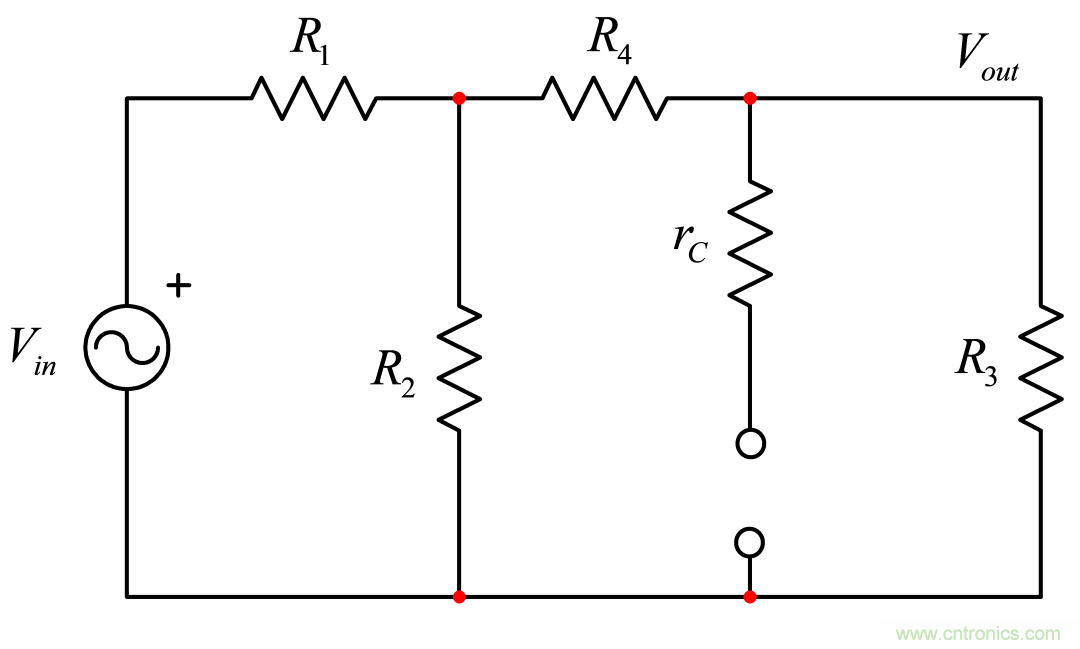
圖5:您斷開直流電路中的電容器,計算這簡單的電阻配置的傳遞函數。
基本就是這些了,我們正錯過零點。我們在前文提到,零點通過阻斷激勵信號的傳播而在電路中表現出來,產生一個無信號的輸出響應(見圖1)。
若我們考慮一個變形的電路–其中C1由代替–如圖6,當激勵源加偏壓于電路,有什么特定的條件意味著無信號響應?無信號響應只意味流過R3的電流為0。這不是短路,而是相當于虛擬的接地。
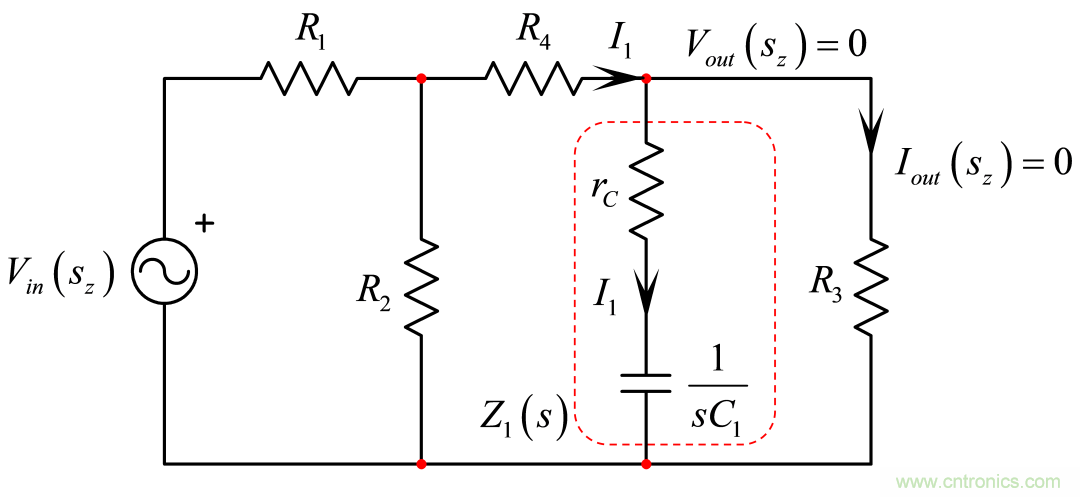
圖6:在這變形的電路中,當串聯的rC和C1轉化為變形的短路,響應消失,R3中無電流流過。
如果在R3中沒有電流,那么串聯的rC和轉化為短路:
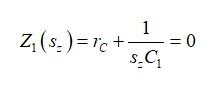 (6)
(6)根sz是我們想要的零點位置:
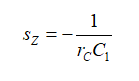 (7)
(7)從而有:
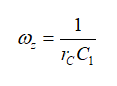 (8)
(8)現在我們可組合所有這些結果,形成以圖3電路為特征的最終的傳遞函數:
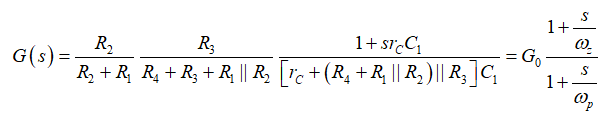 (9)
(9)這就是所謂的低熵表達式,從中您可立即識別靜態增益G0、極點wp和零點wz。高熵表達式將在考慮阻抗分壓器時通過施加大規模外力到原來的電路來獲得,如:
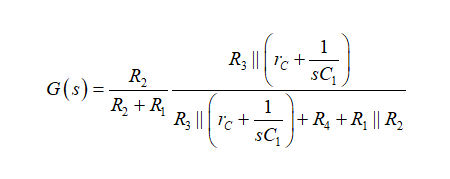 (10)
(10)您不只在推導表達式時可能會出錯—而且將結果格式化到像(9)這樣需要更多的精力。另外,請注意,在這特定的例子中,在寫(9)時我們沒有寫一行代數。如果我們后來發現一個錯誤,那么很容易回到一個單獨的圖紙并單獨修復它。(9)的校正很簡單。現嘗試對(10)進行相同的修正,您可能會從頭開始。
02 FACTs應用于二階系統
FACTs同樣適用于n階無源或有源電路。通過計算狀態變量是獨立的儲能元件的數量來確定電路的階數。若我們考慮一個具有有限的靜態增益H0的二階系統,其傳遞函數可表示如下:
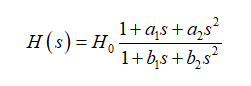 (11)
(11)當H0帶傳遞函數的單位,那么N:D的比值是沒有單位的。這意味著a1和b1的單位是時間[s]。當a1無信號響應,b1的激勵源為零,您將確定的時間常數相加。
對于二階系數,a2或b2,維度是時間的平方[s²],你將時間常數結合為一個產物。然而,在這時間常數產物中,您重用了已經確定為a1或b1的一個時間常數,而二階時間常數的確定需要一個不同的符號:
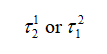 (12)
(12)在這個定義中,您設置標號出現在“冪” 中的儲能元件處于高頻狀態(電容被短路,電感被開路),當我們暫時從電路中移除二階元件端(參見下標),您可從中確定電阻。當a2必須為無信號的輸出和b2的激勵源減為0時,您可運用此法。
當然,當觀察有用時,它總是最快和最高效的得出N的方法。乍一看有點難以理解,但沒有什么不可克服的,我們用幾句話解釋您就會明白。
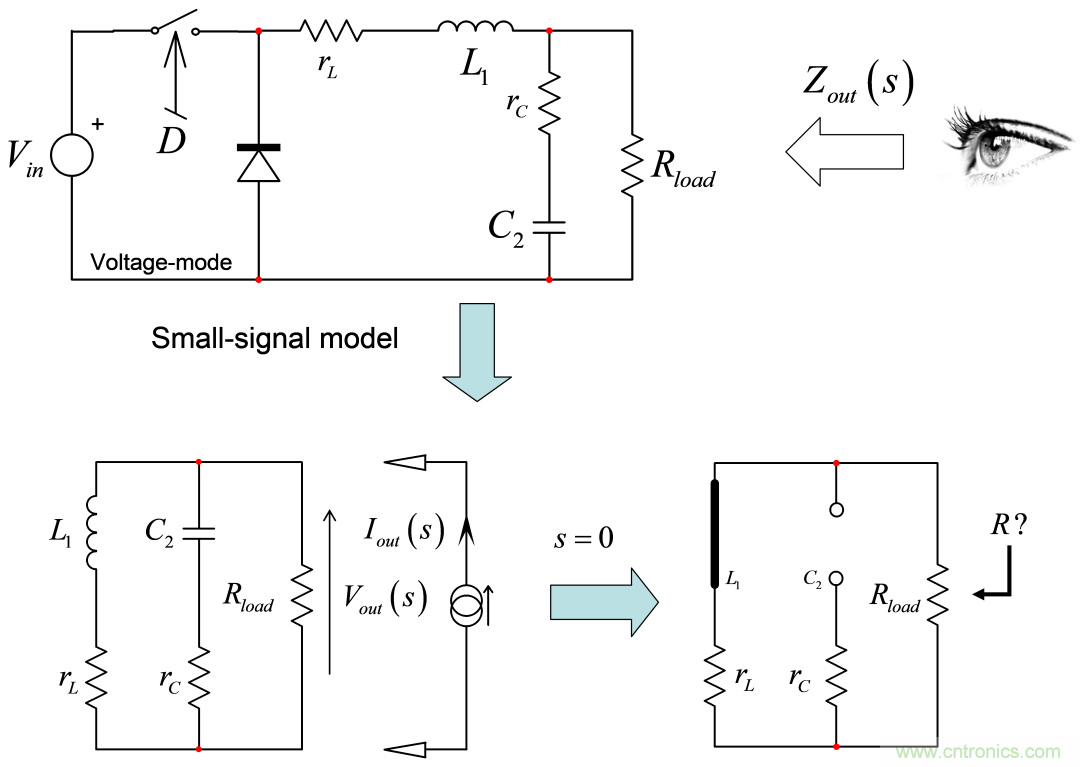
圖7:工作于CCM的降壓轉換器的輸出阻抗的確定是一個很好的例子,演示了FACTs如何簡化分析。
翻譯參考▽
● Voltage-mode:電壓模式
● Small-signal mode:小信號模式
圖7是一個經典的二階濾波器,用于確定在連續導通模式(CCM)中工作的電壓模式降壓轉換器的輸出阻抗。阻抗是連接一個激勵信號Iout與響應信號Vout的一個傳遞函數。
此處,Iout是我們已安裝的測試生成器,而Vout是其兩端產生的電壓。要從(11)中確定各種系數,我們可按照圖2的流程圖,從s = 0開始:如圖所示,電感短路,電容開路。該電路是簡單的,電流源的電阻R0不過是rL和Rload簡單的并列組合:
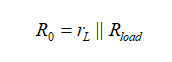 (13)
(13)這個電路中有零點嗎?我們看看圖8所示的變形電路。我們看看當激勵源電流Iout調為零角頻率sz時,什么樣的元件組合將使響應Vout為零。我們可發現兩個變形的短路涉及rL–L1和rc–C2。
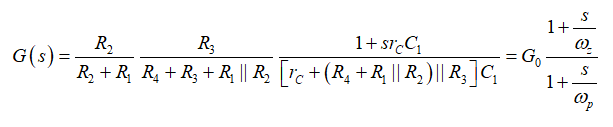
圖8:如果阻抗Z1或Z2轉換為短路,響應Vout為無信號輸出。
立即確定這兩個阻抗的根:
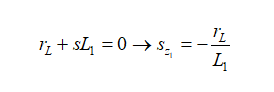 (14)
(14)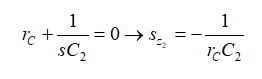 (15)
(15)因此分母N(s)表示為
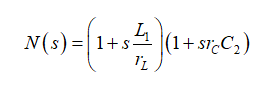 (16)
(16)分母D(s)的一階系數b1是由L1兩端的阻抗提供,而C2處于直流狀態(開路):有t1。然后看驅動C2而L1設置為直流狀態(短路)時的阻抗:得出t2。如圖9所示,從該草圖可立即得出b1的定義:
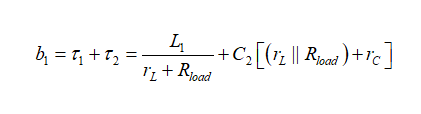 (17)
(17)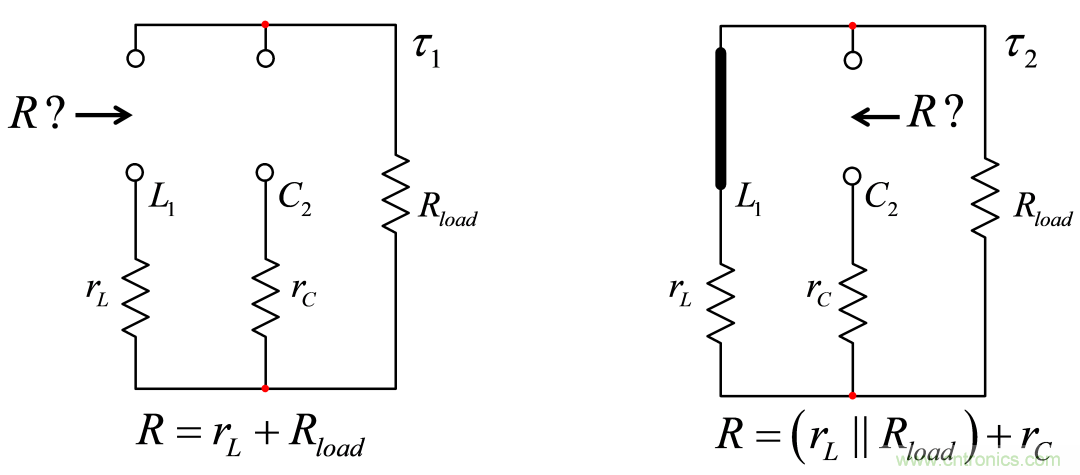
圖9:在選定的組件終端中,當第二個組件處于直流狀態時,您會得出阻抗為多少?
二階系數b2是用(12)中引入的符號來確定的。L1設置在其高頻狀態(開路),驅動C2以得到的阻抗,C2處于高頻狀態(短路),則驅動L1而得到的阻抗。圖10顯示了兩種可能的整理結果。
您通常選擇最簡單的表達式,或避免不確定性的一個,如果有的話(如∞×0或∞/∞)。下面對于b2的兩個定義是相同的,您看上面的是最簡單的:
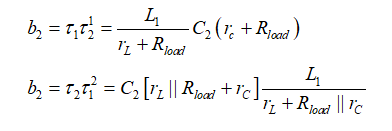 (18)
(18)現在我們有所有的成分來組合最終的傳遞函數,定義為:
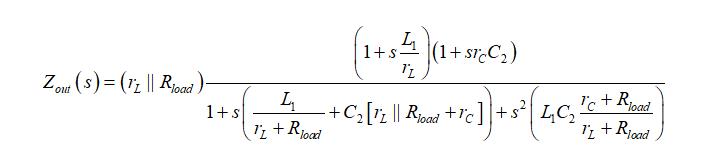 (19)
(19)我們已經確定了這個傳遞函數,而沒有寫一行代數,只是拆分該電路為幾個簡單的草圖個別解決。
此外,正如預期的那樣,(19)已經是一個規范的表達式,您可輕易的看到一個靜態增益、兩個零點和一個可用一個諧振分量w0和一個品質因數Q進一步整理的二階分母。如果不是迅速考慮Z1、Z2 和Rload的并聯組合,我們不可能得到這一結果。
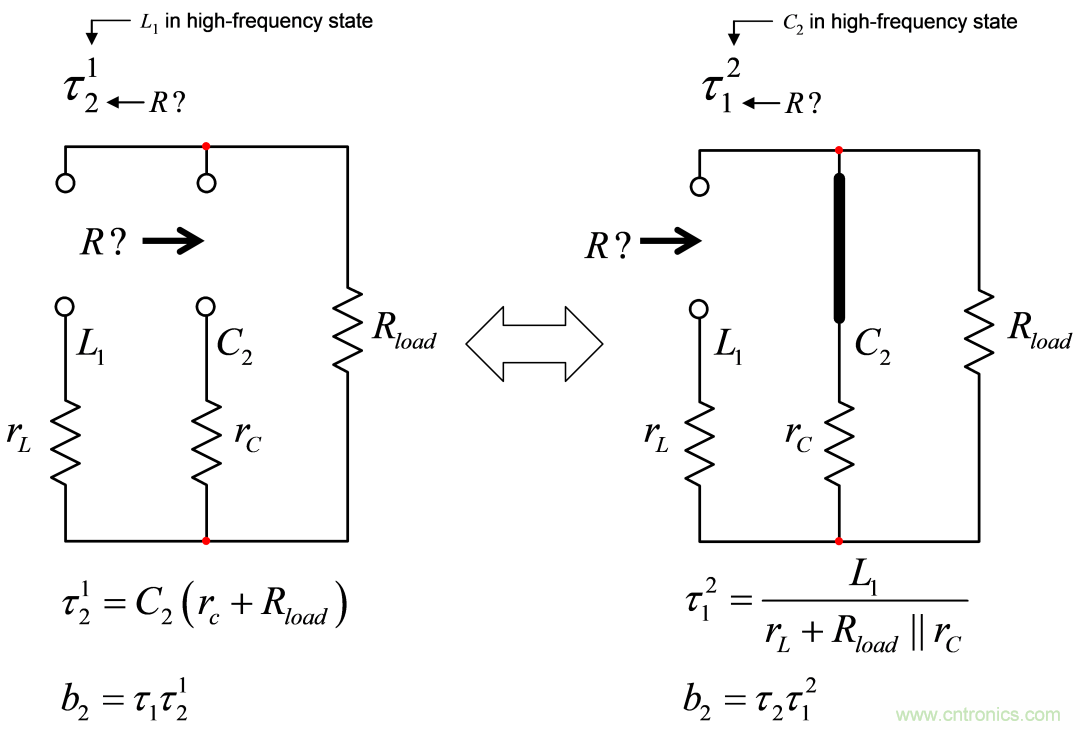
圖10:在選定的組件終端中,當第二個組件處于高頻狀態時,您會得出阻抗為多少?
采用FACTs,通過觀察可導出傳遞函數,特別是對于無源電路。由于電路復雜,包括電壓或電流控制源,觀察起來沒那么明顯,您需要利用經典的網格和節點分析。但FACTs提供了幾個優點:由于您將電路拆分為用于確定最終的多項式表達式系數的小的單個草圖,因此如果在最終的表達式中發現一個錯誤,您總是可以回到一個特定的繪圖并個別修正。
此外,當您確定與傳遞函數的ai和bi相關的項時,您自然會得到一個多項式表達式,而不用投入進一步的精力來收集和重新排列這些項。最后,如[4]所示,在復雜的無源和有源電路中,SPICE對驗證個別極點和零點的計算有很大幫助。
未完待續,下周六見...
References
參考文獻
1. R. D. Middlebrook, Methods of Design-Oriented Analysis: Low-Entropy Expressions, Frontiers in Education Conference, Twenty-First Annual conference, Santa-Barbara, 1992.
2. R. D. Middlebrook, Null Double Injection and the Extra Element Theorem, IEEE Transactions on Education, Vol. 32, NO. 3, August 1989.
3. V. Vorpérian, Fast Analytical Techniques for Electrical and Electronic Circuits, Cambridge University Press, 2002.
4. C. Basso, Linear Circuit Transfer Functions – An Introduction to Fast Analytical Techniques, Wiley, 2016.
5. V. Vorpérian, Simplified Analysis of PWM Converters Using the Model of the PWM Switch, Parts I and II, Transactions on Aerospace and Electronics Systems, vol. 26, no. 3, May 1990.
6. D. Feucht, Design-Oriented Circuit Dynamics, http://www.edn.com/electronics-blogs/outside-the-box-/4404226/Design-oriented-circuit-dynamics
7. D. Peter, We Can do Better: A Proven, Intuitive, Efficient and Practical Design-Oriented Circuit Analysis Paradigm is Available, so why aren''''''''t we using it to teach our Students?,
http://www.icee.usm.edu/ICEE/conferences/asee2007/papers/1362_WE_CAN_DO_BETTER__A_PROVEN__INTUITIVE__E.pdf
8. C. Basso, Fast Analytical Techniques at Work with Small-Signal Modeling, APEC Professional Seminar, Long Beach (CA), 2016, http://cbasso.pagesperso-orange.fr/Spice.htm
9. J. Betten, Benefits of a coupled-inductor SEPIC, slyt411, application note, Texas-Instruments.
10. C. Basso, Switch-Mode Power Supplies: SPICE Simulation and Practical Designs, McGraw-Hill, 2nd edition, 2014.
11. D. Maksimovic, R. Erickson, Advances in Averaged Switch Modeling and Simulation, Power Electronic Specialist Conference Professional Seminar, Charleston, 1999
作者簡介
Christophe Basso
安森美半導體法國圖盧茲 Technical Fellow
他擁有超過20年的電子電路設計經驗,在電力電子轉換領域擁有近30項專利,他原創了許多集成電路芯片,其中代表性為NCP120X系列,它重新定義了電源低待機功耗設標準。
Christophe Basso出版了多部著作,《開關模式 SPICE 仿真和實用設計》深受廣大工程師的歡迎并二次改版,《為線性和開關電源設計控制回路:教程指南》為工程師設計補償和環路穩定性提供了實用指南,《線性電路傳遞函數:介紹快速分析技術》以說教的方式,為學生和需要強大的工具以快速分析日常工作中的復雜電子電路的工程師提供對電路分析的不同角度。
推薦閱讀:







