【導讀】一位工程師已經用了10年了,在發現參考平常的設計實例后深受啟發,決定分享自己的知識——利用PSpice仿真數字濾波器的快速簡單方法講解。
PSpice 已經成為模擬電路仿真使用的行業標準工具。模擬電路具有真實的物理實現,可以用它們的原理示意圖進行仿真,其頻率響應是電路時間常數的結果。與之相反的是,數字濾波器對一系列樣本進行數學運算。數字濾波器的時間常數隱藏在采樣間隔T中。因此數字濾波器一般是通過它們的傳遞函數進行數學仿真,而且為了做到這一點,能夠方便地仿真由采樣率fs引起的采樣延時T=1/fs非常重要,因為這個延時定義和衡量了整個濾波器的響應性能。
通常拉普拉斯變換用于模擬電路的行為建模,因為它將時域變換成為復頻率s域。數字濾波器的頻率響應作為一個特殊例子,可以從拉普拉斯變換的時移理論(延時理論)推導出來。該理論表示,如果時間函數f(t)在時域中被延時了時間T,那么在頻域中的結果要乘以e-sT,見公式(1)。

舉例來說,如果用分子或分母形式將z(-10)寫下來,PSpice將用e-10sT替代z(-10) (s是LAPLACE部分使用的拉普拉斯變量)。公式(3)可以放在包含文件中,或更方便地放在新原理圖模板FUNCTIONS中。
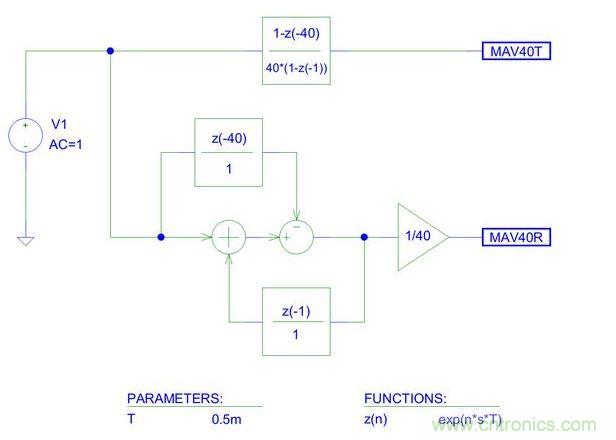
圖1:交流線干擾平均器的PSpice原理圖(梳狀濾波器)。
圖1顯示了用于數字移動平均濾波器交流仿真的PSpice原理圖。移動平均濾波器將拒絕頻率在濾波器零點處的任何信號。
舉例來說,假設采樣頻率fs = 2kHz或T = 0.5ms。為了抑制50Hz的電力線(PL)干擾,來自同一個周期的樣本必須被平均處理。在2kHz采樣率時,一個電力線周期由20ms/0.5ms = 40個樣本組成。平均器可以用傳遞函數直接仿真(輸出MAV40T),或借助接近于其實際算法實現的結構并利用延時模塊、增益模塊以及和差結點進行仿真(輸出MAV40R)。該仿真在電力線干擾的所有諧波處都有凹槽,如圖2所示。
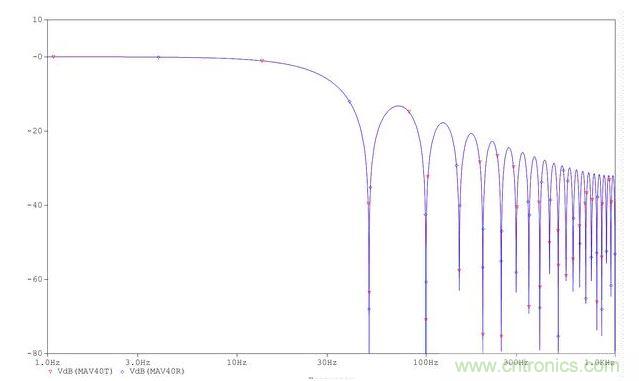
圖2:平均器的頻率響應。
上述方法既快又容易。我已經用了10年了,在發現參考1中的設計實例后深受啟發,決定分享我的知識。







